Bonnie M. Stewart war vierzig Jahre lang, von 1940 bis 1980, Professor für Mathematik an der Michigan State University. Als er in den Ruhestand ging, gab es das Internet noch nicht; kein Wunder, dass die Website seiner alten Universität nicht viel über ihn zu sagen weiß. Er ist im April 1994 im Alter von 79 Jahren gestorben.

Aber in der Papierwelt hat er eine Spur hinterlassen, die ihresgleichen sucht. Er hat 1970 (2., erweiterte Auflage 1980) ein Buch mit dem Titel "Adventures among the toroids" veröffentlicht, dessen 256 Seiten von vorn bis hinten handgeschrieben sind. Na ja, es ist ein formelreicher und von unzähligen Zeichnungen durchsetzter Text, und 1970 gab es noch keinen Computer-Textsatz, geschweige denn Formelsatz; da ist mit der Hand zu schreiben eine vielleicht kauzige, aber durchaus sinnvolle Möglichkeit, unmäßiger Mühe und entsprechenden Kosten bei der Drucklegung aus dem Wege zu gehen. Aber Stewart hat den Ehrgeiz besessen, nicht nur saubere Buchstaben zu zeichnen, sondern sich auf eine bestimmte Schriftart festgelegt: Chancery Script, und vor allem: Blocksatz geschrieben, bis in die letzte Zeile! Jeder Absatz ist ein säuberlich mit Zeichen gefülltes Rechteckskästchen, es sei denn, Bilder ragten in den Text hinein.

Welch unglaubliche Mühe das gekostet hat, kann man nur erahnen. Ganz am Ende des Buches bittet der Autor seine Leser, ein paar Merkwürdigkeiten zu entschuldigen. Er hatte geforscht und geschrieben im Wechsel, und ein paar Ausrufe des Entzückens über die Vielfalt der soeben entdeckten Polyeder hätte er später gestrichen, als er einen noch weit reichhaltigeren Polyeder-Zoo entdeckte – wenn er dafür nicht mehrere Seiten hätte neu schreiben müssen. Schauen Sie sich das Buch an, wenn Sie das Staunen lernen wollen! Es ist nicht ganz einfach dranzukommen; aber mit Geduld und Fernleihe geht es.

Stewarts Bereitschaft zu unglaublicher Fleißarbeit, verbunden mit einem gewissen Hang zur Vollständigkeit, kennzeichnet auch seine Forschungen. Er interessierte sich für Polyeder, die nicht nur einfach zusammenhängend sind, sondern Henkel, Löcher, Tunnel oder ähnliches haben dürfen. Damit es nicht ganz beliebig wurde, legte er sich zusätzlich darauf fest, dass sämtliche Seitenflächen regelmäßige Vielecke sein sollten. Die Ecken mussten nicht alle gleich sein – das war die einschränkende Bedingung für die archimedischen Körper –, und vor allem: Konvexität war nicht verlangt, denn dieses Feld hatte der von Stewart bewunderte Norman Johnson bereits abgegrast (siehe die letzte Folge). Und Löcher sind bei konvexen Körpern per definitionem ausgeschlossen.

Die erste Idee ist: Man setze irgendwelche elementaren Bauklötze Fläche auf Fläche aufeinander. Immerhin hat Norman Johnson 92 konvexe Bauklötze bereitgestellt, die ausschließlich von regelmäßigen Vielecken begrenzt sind (siehe die letzte Folge). Da kommt es oft genug vor, dass Dreieck auf Dreieck oder Quadrat auf Quadrat passt. Ketten von Oktaedern sind ein gutes Beispiel; Ketten von Würfeln weniger. Denn dabei geraten unweigerlich zwei Quadrate aus benachbarten Würfeln direkt nebeneinander in eine Ebene – und schon sind es keine zwei Quadrate mehr, sondern ein längliches Rechteck. Ähnliches passiert einem bei der Kombination Tetraeder auf Oktaeder (vergleiche Folge 1). Aber Oktaeder sind sehr gut verwendbare Bauklötze. Man kann sie nicht nur zu Ketten zusammensetzen, sondern auch zu Ringen – und siehe da, da ist das erste Loch! Ich habe Ihnen die Oktaederringe in der Folge 7 "Unendliche Polyeder" vorgestellt, zusammen mit einigen anderen Bauvorschriften, die erstens Ringe liefern und zweitens Zusammensetzungen von beliebig vielen Ringen. Steven Dutch, der auf seiner Website etliche von ihnen der Öffentlichkeit präsentiert, bezieht sich ausdrücklich auf Vorarbeiten von Bonnie Stewart.

Wo zwei Quadrate von Würfeln nicht aneinander stoßen dürfen, kann man auf eines von ihnen gleich noch einen Würfel aufsetzen, und so weiter. Es gibt Stapel aus lauter Würfeln, die Fläche an Fläche aneinandergestapelt sind und in denen nirgends zwei Quadrate in derselben Ebene benachbart sind – jedenfalls nicht an der sichtbaren Außenseite des Stapels. Das ganze Ding ist dann unweigerlich eine mehr oder weniger gigantische Stufenpyramide (siehe ebenfalls Folge 7).

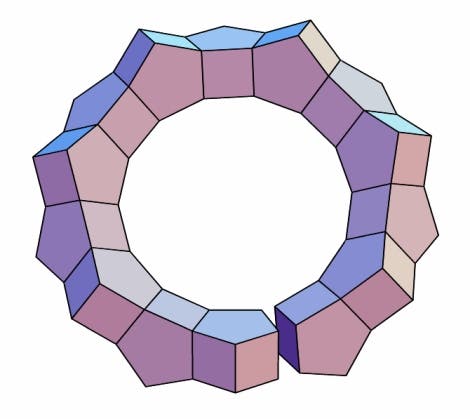
Hat man ein hübsches Muster von Vielecken in der Ebene, zum Beispiel ein Bienenwabenmuster aus lauter Sechsecken, dann kann man es räumlich machen, indem man die ganze Ebene "andickt". Aus den Sechsecken werden so sechsseitige Prismen mit quadratischen Seitenflächen. Für Stewarts Zwecke sind sie zwar ungeeignet, die Deckelflächen benachbarter Sechsecke liegen ja in einer Ebene. Aber dem ist abzuhelfen. Nehmen Sie drei sechsseitige Prismen in Bienenwabenposition, trennen Sie sie und schieben Sie an jeder Trennfläche ein sechsseitiges Prisma ein – aber diesmal nicht ein liegendes, sondern ein quer stehendes, Quadratfläche an Quadratfläche! Schon haben Sie einen Ring aus sechs sechsseitigen Prismen. Der ist überdies beliebig fortsetzbar (das ursprüngliche Bienenwabenmuster bedeckt ja die ganze Ebene), also ist der Zahl der Löcher keine Grenze gesetzt.

Es müssen auch nicht unbedingt sechsseitige Prismen sein. Als stehende Zwischenstücke taugen alle Prismen mit geraden Seitenzahlen von 6 und größer. Für die liegenden Prismen sind auch ungerade Seitenzahlen zugelassen. Na ja, man kann die Ebene nicht lückenlos mit Fünf- oder Siebenecken pflastern; aber das ist hier auch gar nicht dringend. Wichtig ist: 2n Stück regelmäßige n-Ecke lassen sich zu einem geschlossenen Ring zusammenlegen, und solche Ringe lassen sich auf viele Weisen ineinander hängen. (Vielleicht nicht periodisch, aber das ist eine andere Geschichte.) Dasselbe Rezept wie oben: andicken und aneinander grenzende Deckflächen mit eingeschobenen hochkant stehenden Sechserprismen auf Abstand halten, funktioniert auch für diese Anordnungen.

Das müsste man doch verallgemeinern können, auf einen Ring nur aus Fünferprismen mit der Eigenschaft, dass nirgends benachbarte Fünfecksflächen in eine Ebene zu liegen kommen. Dachte ich. Es sah auch zunächst ganz gut aus; aber dann hat der (errechnete) Ring aus 14 Fünferprismen eine Lücke, statt sich richtig zu schließen. Pech gehabt. Wenn der Ring sich hätte schließen lassen, ich bin sicher, er wäre Stewarts universeller Aufmerksamkeit nicht entgangen.

Diese sehr ausgedehnten Zusammensetzungen aus elementaren Bausteinen sind in Stewarts Werk nichts weiter als ein (nicht unbedeutender) Abstecher. Seine eigentliche Aufmerksamkeit gilt Körpern, die nicht durch "Addition", sondern auch durch "Subtraktion" elementarer Bausteine entstehen.

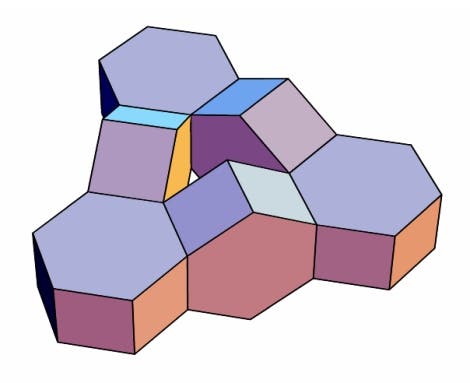
An den einfachsten Beispielen sieht man am ehesten, was gemeint ist. Ein sechsseitiges Prisma ist genau so hoch wie ein dreiseitiges. Kein Wunder: Alle Prismen haben die gleiche Höhe, nämlich eine Kantenlänge. (Alle Bauklötze unseres gedachten Sortiments haben eine einheitliche Kantenlänge.) Eins von Johnsons 92 Polyedern ist die dreiseitige Kuppel: Boden Sechseck, Deckel Dreieck, dazwischen die schrägen Wände abwechselnd Dreiecke und Quadrate. So eine Kuppel passt prima auf ein sechsseitiges Prisma, und ein dreiseitiges Prisma passt prima auf eine Kuppel. Das gibt zwei "Türme" (na ja, Türmchen) aus je zwei Bauklötzen, die nicht nur genau gleich hoch sind, sondern auch dieselbe Boden- und Deckelfläche haben. Außerdem ist der erste an jeder Stelle zwischen Boden und Deckel ausladender als der zweite.

Jetzt kommt's. Man "subtrahiere" den zweiten Turm vom ersten. Das heißt, man bringt sie in Gedanken auf denselben Platz, sodass ihre Boden- und Deckelflächen zusammenfallen, und bilde die mengentheoretische Differenz: alle Punkte vom ersten Turm, die nicht zum zweiten gehören. Das Ergebnis ist ein Turm mit Tunnel und damit vom Geschlecht 1.

Geschlecht? Na ja, so nennen das die Topologen. Die englische Übersetzung ist nicht "sex", sondern "genus"; ein harmloses Wort wie "Sorte" oder "Klasse" hätte die Sache auch getroffen. Das Geschlecht eines Körpers (genauer: das Geschlecht seiner Oberfläche) ist eine Zahl, die angibt, wie oft man ihn durchschneiden kann, ohne dass er in zwei Teile zerfällt. Die üblichen Wald- und Wiesen-Polyeder haben das Geschlecht null. Unser Turm-Differenz-Körper hat das Geschlecht 1, weil er über genau ein Loch verfügt.

Eigentlich kommt es einem Topologen auf die genaue Gestalt seiner Gegenstände nicht an, im Gegenteil: Ob und wie sie deformiert sind, ist für ihn belanglos (solange nicht geschnitten und/oder verklebt wird), und ob sie von lauter regelmäßigen Vielecken begrenzt sind, erst recht. Aber inoffiziell stellen sich die Topologen ihre Gebilde in gewissen Lieblingsformen vor: ein Wald- und Wiesen-Polyeder als Sphäre (Kugeloberfläche) und die vom Geschlecht 1 als Torus (Autoschlauch, Calamares-Ring oder so). Deswegen nennt Stewart seine Lochkörper "Toroide".

Es gibt viele Kombinationen von Johnson-Bauklötzen, auf die sich das geschilderte Grundrezept von Stewart anwenden lässt. Noch so eine einfache: Ein Oktaeder, auf eine seiner Dreiecksflächen gelegt, ist genau so hoch wie eine dreiseitige Kuppel. Zwei solche Kuppeln, mit den weiten (sechseckigen) Öffnungen aufeinander gelegt, haben dreieckige Boden- und Deckelflächen in genau dem richtigen Abstand: Man grabe einen Tunnel aus zwei Oktaedern hinein – fertig! Allerdings muss man die äußeren Kuppeln "ortho" (Quadrat gegen Quadrat) und nicht "gyro" (Quadrat gegen Dreieck) aufeinander setzen. Sonst sind Boden- und Deckeldreieck gegeneinander verdreht, was man mit dem Oktaederturm nicht machen kann.

Oder: Außen ein Würfelstumpf, das heißt ein Würfel so milde enteckt, dass von den Quadraten noch Achtecke übrig bleiben. Innen eine vierseitige Kuppel, darauf ein Würfel (der viel kleiner ist als der äußere enteckte), darauf kopfunter eine vierseitige Kuppel, sodass der Innenkörper als Boden- und Deckelfläche je ein Achteck hat, wie der Würfelstumpf. Passt auch.

Für Stewarts Rezept müssen also erstens die gemeinsamen Außenflächen (die bisher Boden und Deckel waren) übereinstimmen und zweitens die Summe der Höhen. Konsequenterweise steht im Anhang des Buches eine Tabelle der Höhen aller Johnson-Körper, in den verschiedenen Orientierungen. Und wundersamerweise gibt es unglaublich viele Türme aus Körpern mit übereinstimmender Höhensumme. Entsprechend wächst die Anzahl der Toroide ins Unermessliche.

Die "Bilunabirotunda" (Johnsons Nummer 91), auf eines seiner Fünfecke gelegt, ist ein schräger Vogel in jeder Hinsicht, denn ihre gegenüberliegenden Fünfecke liegen gegeneinander versetzt. Ein Tunnel, an dem sie beteiligt ist, hat keine schöne Mittelachse mehr, sondern geht mehrfach um die Ecke. Da gibt es Tunnel, die winden sich im Inneren ihres gastgebenden Körpers umeinander wie zwei Würmer, die sich nicht ausstehen können, in ein und demselben Apfel.

Es kommt auch vor, dass Ein- und Ausgangsöffnung eines Tunnels einander nicht gegenüberliegen, oder allgemeiner noch, dass in die Oberfläche des Außenkörpers mehr als zwei Löcher gegraben werden. Am schönsten finde ich die Körper, deren Löcher die ursprüngliche Symmetrie des Außenkörpers wahren, sodass der Hohlkörper mit Fug und Recht ein Vollmitglied der jeweiligen Familie genannt werden kann.

Von den Symmetrie brechenden Körpern gibt es mehr als von den Symmetrie wahrenden; das ist immer so. Wenn man auf Einhaltung der Symmetrie besteht, schrumpfen die riesengroßen Anzahlen Stewarts auf ein überschaubares (immer noch bewundernswertes) Maß zusammen. Robert Webb, der Autor des "Polyhedron Navigator" (siehe Folge 14), hat zwei von ihnen ins Internet gestellt, was mir besser geholfen hat, ihren Aufbau zu verstehen, als Stewarts Buch.

Der eine ist der "ausgehöhlte Dodekaederstumpf" ("drilled truncated dodecahedron" bei Webb). Der Dodekaederstumpf besteht aus zwölf Zehnecken statt der Fünfecke des Dodekaeders und Dreiecken an den Stellen, wo vor dem Entecken die Ecken des Dodekaeders waren. Man grabe an der Stelle jedes Zehnecks eine Grube in Form einer fünfseitigen Kuppel, vertiefe dann jede Grube durch ein fünfseitiges Antiprisma, und siehe da: Die zwölf Schächte treffen sich! Die Fünfecke am Boden jedes Schachtes sind die Flächen eines Dodekaeders, und wenn man das auch noch ausgräbt, dann hat man einen Hohlkörper von wahrlich bedeutendem Geschlecht: 11! Fünfecke sind in ihm allenthalben präsent, aber nur als Löcher. Unter seinen Seitenflächen kommt kein einziges Fünfeck vor, nur Dreiecke und Quadrate.

Der andere Körper ist vom gleichen Geschlecht und darf sich ebenfalls der Familie der Fünfzähligen zugehörig fühlen. Er gibt Anlass, das schöne Wort Ikosi-Dodekaeder ausgiebig buchstabieren zu lernen. Denn unter den archimedischen Körpern gibt es erstens das Rhomben-Ikosi-Dodekaeder und zweitens das große Rhomben-Ikosi-Dodekaeder. Letzteres trägt seinen Namen zu Recht, denn es ist – bei gleicher Kantenlänge – in der Tat größer als sein ansonsten gleichnamiger Bruder. Der Kleine besteht aus Fünfecken, Quadraten und Dreiecken, der Große aus Zehnecken, Quadraten und Sechsecken. Und wenn man den Kleinen genau mitten in den Großen setzt, dann – Sie ahnen es schon – kann man an der Stelle jedes Zehnecks eine Grube graben, deren fünfeckiger Boden genau mit den Fünfecken des Kleinen zusammenfällt. In diesem Fall ist diese Grube eine fünfseitige Rotunde, und die ist nichts anderes als – drittens! – ein halbes Ikosidodekaeder. So kommt das edle Stück bei Robert Webb zu seinem Namen "rotunda-drilled great rhombicosidodecahedron" ("rotunden-ausgehöhltes großes Rhomben-Ikosi-Dodekaeder"). Genießen Sie seine Schönheit und vergessen Sie darüber den Bandwurm-Namen.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft

Literaturhinweise nur für diese Folge:
Bonnie M. Stewart: Adventures among the toroids. A study of orientable polyhedra with regular faces. 2. Auflage, Selbstverlag, Okemos (Michigan) 1980.

Zu den beiden zuletzt beschriebenen Körpern biete ich Karton-Bausätze an:
www.poeppe-online.de.