Ich esse leidenschaftlich gerne Schokolade. Wenn die letzte kleine Praline vor mir liegt, wünsche ich mir häufig, man könnte sie einfach verdoppeln – am besten auch noch so, dass keine zusätzlichen Kalorien hinzukommen. Nimmt man den Satz von Banach und Tarski ernst, dann sollte das zumindest aus mathematischer Sicht kein Problem sein.

Doch bevor Sie jetzt in Jubel ausbrechen, muss ich Sie vorwarnen: Ganz so einfach wird es leider nicht. Strengen mathematischen Prinzipien zufolge ist es zwar möglich, eine Kugel in ihre Bestandteile zu zerlegen, in sechs Teile zu sortieren und zu zwei neuen Kugeln zusammenzusetzen, die jeweils das gleiche Volumen haben wie die erste. Aber realistisch umsetzbar ist das Ganze wohl kaum. Dennoch: Das Ergebnis, das die polnischen Mathematiker Stefan Banach und Alfred Tarski 1924 veröffentlicht haben, ist faszinierend und verdient es durchaus, vorgestellt zu werden.

Dass es überhaupt möglich ist, das Volumen einer Kugel zu verdoppeln, verdanken wir dem Konzept der Unendlichkeit. Diese unvorstellbare Größe ist meistens am Werk, wenn scheinbare Paradoxa in der Mathematik auftauchen. Das ist auch nicht weiter verwunderlich, denn das Unermessliche entzieht sich unserer Vorstellungskraft.

Unendlich ist nicht immer gleich unendlich

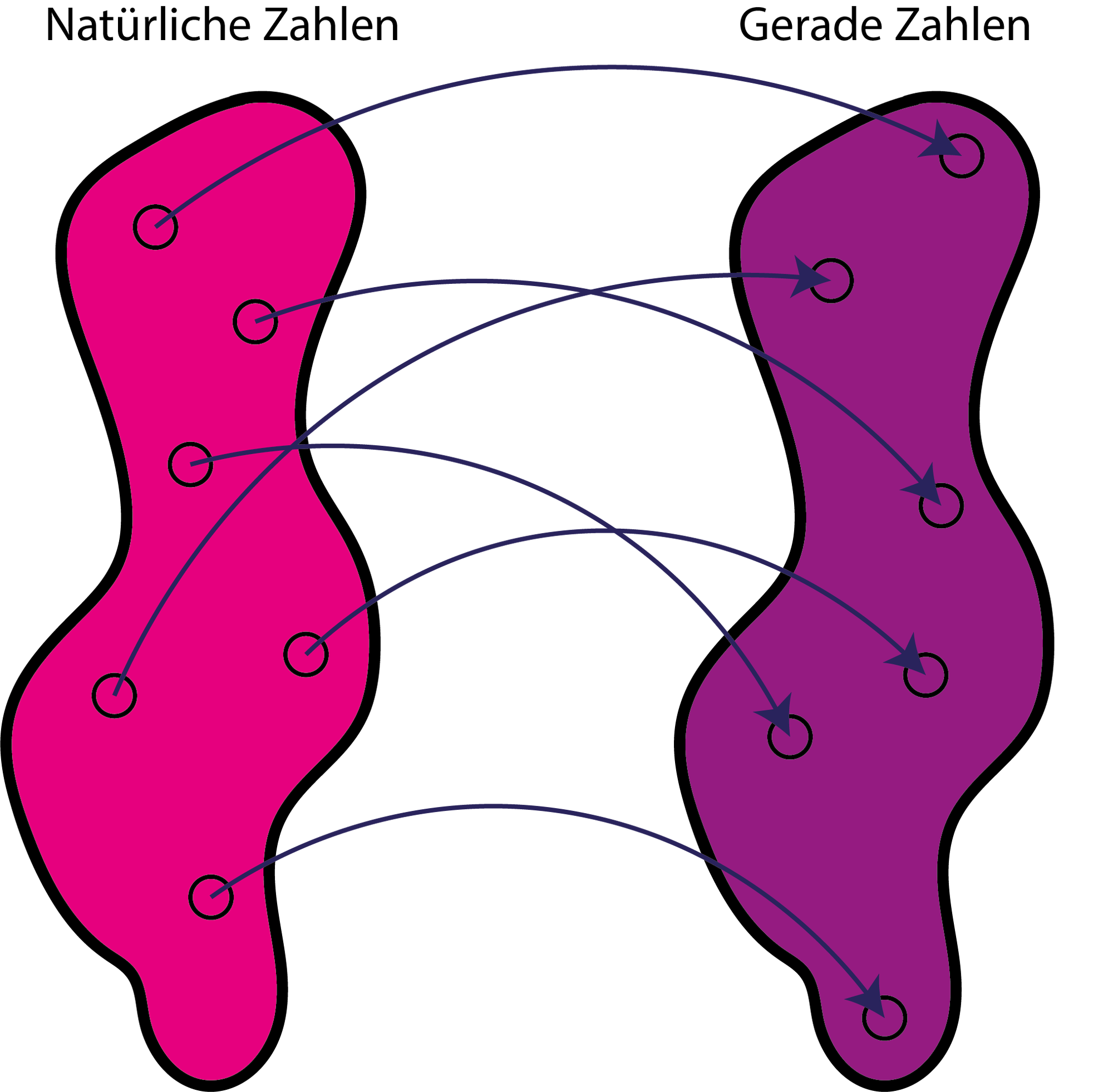
Nehmen wir einmal die natürlichen Zahlen: Dass es unendlich viele davon gibt, ist noch recht leicht nachzuvollziehen. Und auch die geraden Zahlen sind unbegrenzt. Doch entgegen der Intuition existieren genau so viele gerade wie natürliche Zahlen; man spricht von einer abzählbaren Unendlichkeit. Grund dafür ist, dass man jeder geraden Zahl g eine natürliche n (und umgekehrt) zuordnen kann, etwa 2 → 1, 4 → 2, 6 → 3, 8 → 4 und so weiter. Da diese Abbildung immer aufgeht und niemals ein Wert übrig bleibt, sind die Mengen folglich gleich groß.

Das Umgekehrte gilt allerdings auch: Wenn es keine Eins-zu-Eins-Zuordnung zwischen zwei Mengen gibt, dann sind sie unterschiedlich groß. Das ist zum Beispiel bei den reellen Zahlen (jene, die den Zahlenstrahl aufspannen und irrationale Werte wie Pi oder √2 enthalten) und den natürlichen der Fall: Die Menge der reellen Zahlen übersteigt die der natürlichen.

Tatsächlich sind es ähnliche Überlegungen, die dazu führen, dass sich das Volumen einer Kugel ohne Zauberei durch bloße Umsortierung ihrer Punkte verdoppeln lässt. Dafür startet man zunächst mit der Kugeloberfläche und teilt die Punkte in unendlich viele unendlich große Mengen ein.

Punkte sortieren

Der erste Schritt ist einfach: Man wählt irgendeinen Punkt auf der Kugel aus und ordnet ihn einer Menge M₁ zu. Anschließend überlegt man sich zwei irrationale Winkel (die sich also nicht als Bruch darstellen lassen) α und β, Ersterer entspricht Drehungen um die Nord-Süd- und Letzterer um die Ost-West-Achse. Dann rotiert man die Kugel entlang einer dieser Achsen um den dazugehörigen Winkel. So landet man bei einem neuen Punkt, den man ebenfalls in M₁ schreibt. Anschließend macht man weiter, dreht die Kugel immer wieder nach oben, unten, links oder rechts um die entsprechenden Winkel und erzeugt damit eine unendlich große Menge M₁ an Punkten. Die einzige Beschränkung ist, dass man die Kugel nicht vor- und gleich darauf wieder zurückdrehen darf (man darf Rotationen nicht rückgängig machen). Da die Drehwinkel irrational sind, landet man niemals zweimal am selben Ort. Die Menge enthält also nur unterschiedliche Punkte.

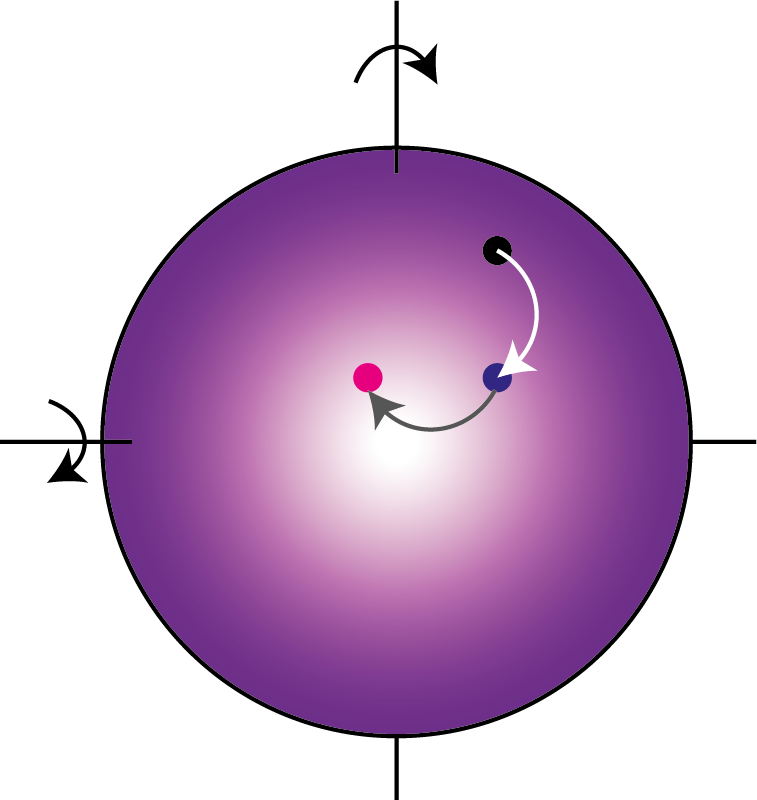
Hat man auf diese Weise – wenn man alle möglichen Rotationen durchgeht – jeden Punkt auf der Kugeloberfläche aufgegriffen? Nein. Der Grund dafür ist folgender: All die durchgeführten Drehungen lassen sich nummerieren. Damit existiert eine Abbildung zwischen den natürlichen Zahlen und der Menge M₁, das heißt, sie enthalten gleich viele Elemente, und zwar abzählbar unendlich viele.

Eine Kugeloberfläche umfasst hingegen mehr Punkte; wie bei den reellen Zahlen unterscheidet sich ihre Unendlichkeit von jener der natürlichen Zahlen. Mathematiker sprechen von überabzählbar vielen Elementen. Daher ist es unmöglich, eine Eins-zu-Eins-Abbildung zwischen einer Kugeloberfläche und den natürlichen Zahlen zu erstellen: Würde man versuchen, die Punkte auf einer Kugel aufzulisten (was einer solchen Eins-zu-Eins-Zuordnung gleichkäme), ließen sich stets weitere Punkte finden, welche die Liste noch nicht enthält.

Wenn also die Unendlichkeit der Kugeloberfläche überabzählbar ist und die der Menge M₁ abzählbar, dann kann M₁ nicht alle Punkte umfassen. Daher wiederholt man die oben geschilderte Prozedur der Drehungen mit einem anderen Startpunkt auf der Kugel, der nicht in M₁ ist. Daraus lässt sich eine neue Menge M₂ konstruieren. Anschließend macht man das Gleiche für jeden weiteren Punkt auf der Kugel, der nicht in den vorangehenden Mengen enthalten ist. Damit erhält man überabzählbar unendlich viele Mengen M mit je abzählbar unendlich vielen Elementen.

Sechs Gruppen verschaffen Überblick

Das klingt ziemlich verwirrend. Um das Ganze übersichtlicher zu gestalten, wählt man einzelne Punkte aus den Mengen aus und sortiert sie in sechs Gruppen. Dass dies überhaupt erlaubt ist, ermöglicht das so genannte Auswahlaxiom, ein Grundpfeiler der Mathematik. Dabei handelt es sich um eine unbewiesene Aussage, die man als wahr annimmt, um daraus (zusammen mit anderen Axiomen) alle mathematischen Zusammenhänge herzuleiten. Das Auswahlaxiom besagt, dass man aus einer Sammlung nichtleerer Mengen stets ein Element aus jeder dieser Mengen auswählen kann.

Vier der sechs Gruppen entsprechen den vier Himmelsrichtungen: die Nord-, Ost-, Süd- und Westgruppe. Sie enthalten alle Punkte P_j aus den Mengen M, deren letzte Drehung in die dazugehörige Richtung zu P_j führte. Wenn also eine südliche Rotation P₃₄₅ erzeugt hat, landet P₃₄₅ in der Südgruppe.

Es gibt jedoch Punkte, die durch unterschiedliche vorangehende Rotationen entstehen können, nämlich die Pole. Der Nordpol bleibt bestehen, wenn man die Kugel nach Westen oder Osten dreht – somit könnte er in mehreren Gruppen auftauchen. Daher sortiert man diese Spezialfälle in eine fünfte Kategorie ein. Darüber hinaus bildet man eine sechste Gruppe, die alle Startpunkte enthält.

Bisher hat man die Punkte der Kugeloberfläche bloß umsortiert, aber noch nicht vervielfältigt. Nun kommt der Trick, der dazu führt, dass sich die Elemente verdoppeln: Wenn man eine der vier Himmelsrichtungen-Gruppen (deren Punkte anschaulich gesehen eine Kugel bilden) geschickt dreht, umfasst sie am Ende mehr Elemente als zuvor. Das mag unglaublich erscheinen, ist aber wieder einmal bloß ein ungewöhnlicher Aspekt von Unendlichkeiten.

Um das nachzuvollziehen, kann man mit der Ostgruppe beginnen, die alle Punkte enthält, die durch eine Ostdrehung erzeugt wurden. Anschaulich lassen sich die Punkte durch eine Zeichenfolge codieren, welche die entsprechenden Drehungen aufzählt, die vom Startpunkt bis zu den betrachteten Endpunkten führten (wobei r, l, o, u für rechts, links, oben, unten stehen). Zum Beispiel sind r, ro, ru, rr, roo, ror, rol, rur, ruu, rul und so weiter alle Elemente der Ostgruppe. Man liest die Drehungen von rechts nach links, deshalb enthält die Ostgruppe alle Zeichenfolgen, die mit r beginnen. Die Nordgruppe umfasst hingegen alle mit o startenden Buchstabenketten: o, oo, or, ol, oro, oru und so weiter. Dreht man die Ostgruppe nun um β in westliche Richtung, macht man die letzte Drehung der darin enthaltenen Punkte rückgängig. Aus r, ro, ru, rr, roo, ror, rol, rur, ruu, rul wird lr, lro, lru, lrr, lroo, lror, lrur, lruu, lrul und da sich lr-Verbindungen gerade aufheben, entsteht: keine Rotation, o, u, r, oo, or, ol, ur, uu, ul und so weiter. Damit enthält die gedrehte Gruppe jeweils unendlich viele Punkte, die mit einer Nord-, Süd- oder Ostrotation enden. Zudem umfasst sie alle Startpunkte (keine Rotation) auf der Kugel.

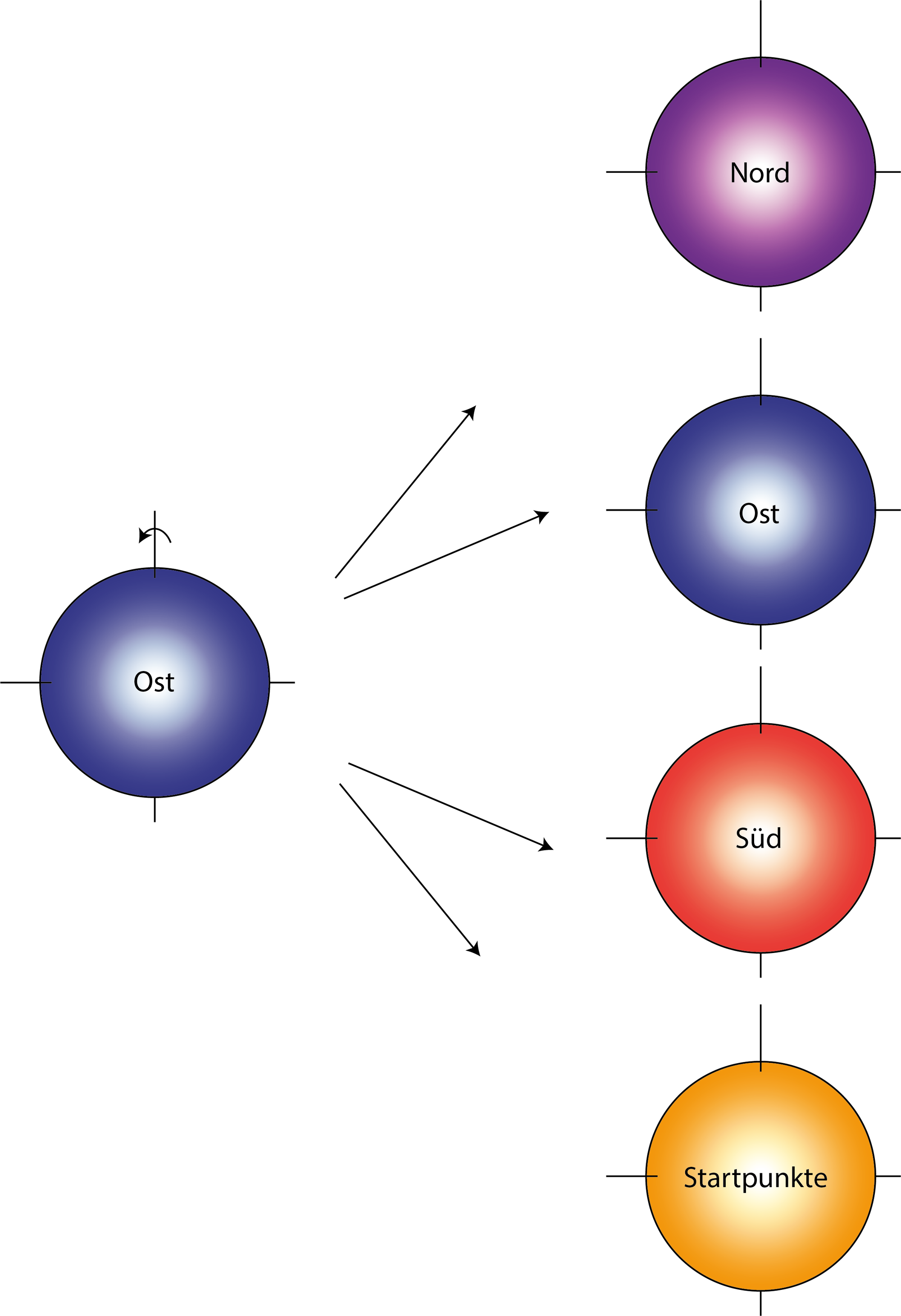
Das heißt, die nach Westen rotierte Ostgruppe enthält nun die ursprüngliche Ostgruppe, die Nord- und die Südgruppe sowie die Gruppe der Startpunkte. Damit hat man insgesamt drei der sechs Gruppen verdoppelt (Nord-, Süd- und Startgruppe). Um die übrigen drei auch zu duplizieren, wiederholt man das Ganze mit der Nordgruppe: Man dreht sie nach Süden und erhält damit die Ost-, West- und die Nordgruppe sowie nochmals die Startpunkte. Letztere taucht also einmal zu viel auf. Um das zu vermeiden, entfernt man aus der ursprünglichen Nordgruppe vor der Drehung alle Punkte, die zu den Startpunkten führen würden, und fügt sie zur Südgruppe hinzu. Damit hat man jede Gruppe exakt verdoppelt – bis auf jene mit den Polen.

Das Ungewünschte in die Unendlichkeit verschieben

Hier bedient man sich eines weiteren Tricks, der mit Unendlichkeiten zu tun hat. Stellen Sie sich vor, Sie besitzen eine unendlich lange Perlenkette, doch am Anfang fehlt eine Perle. Dann können Sie die benachbarte Perle auf die Lücke ziehen, ebenso wie die nachfolgende und so weiter. Am Ende haben Sie wieder eine lückenlose Kette – der freie Platz ist nämlich in die Unendlichkeit gerückt. Gleiches lässt sich mit den Fehlstellen an den Polen machen: Man verfrachtet die Lücken in die Unendlichkeit, indem man die Punkte verschiebt und immer neue Punkte nachrücken. Die vorgestellten Methoden mögen unglaublich klingen, doch mathematisch gesehen sind sie alle erlaubt und stellen keine Probleme dar. Damit hat man es also geschafft, die Oberfläche einer Kugel ganz ohne Zauberei zu verdoppeln.

Das ursprüngliche Ziel war es jedoch, eine ganze Kugel – und nicht nur deren Oberfläche – zu vervielfältigen. Glücklicherweise lässt sich das Ergebnis auf die volle Kugel übertragen. Dafür kann man sich zu jedem Punkt auf der Oberfläche einen Strahl vorstellen, der ihn mit dem Mittelpunkt der Kugel verbindet. Die geschilderten Vorgänge wendet man dann auf den gesamten Strahl an – und landet beim gleichen Ergebnis: Aus einer Kugel mit Volumen V entstehen zwei identische Kopien, die ebenfalls das Volumen V haben.

Meine geliebte Praline lässt sich auf diese Weise aber leider nicht verdoppeln: Der Versuch wird daran scheitern, dass sie zwar aus unvorstellbar vielen (Aber- und Abermilliarden) Atomen besteht – aber ihre Bestandteile dennoch endlich sind. Somit kann man die geschickten Tricks leider nicht auf Schokolade anwenden – eine Lücke lässt sich darin nun einmal nicht ins Unendliche verschieben. Schade eigentlich.

Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!