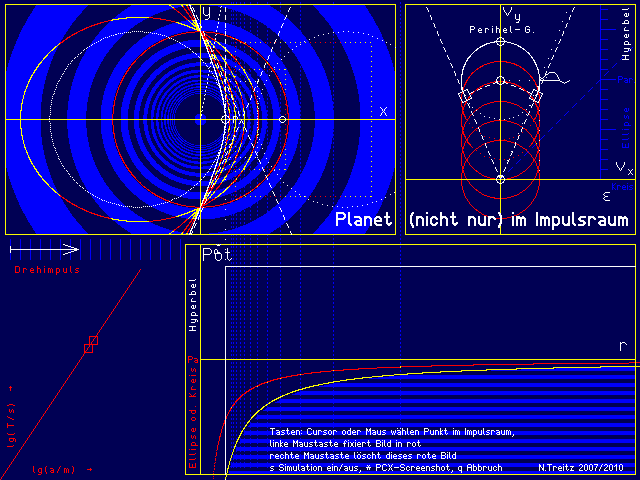
Planet

Dieses Programm behandelt das sogenannte Einkörperproblem, d.h. zwei Punktmassen mit "unendlich" großem Massenverhältnis (m/M =0), die sich allein unter dem Einfluss gegenseitiger newtonscher Schwerkraft bewegen und die dabei in einem gemeinsamen Schwerpunktsystem beschrieben werden, das sich gegen den Rest der Welt nicht dreht (d.h. ein Inertialsystem ist). Das weitaus schwerere Objekt wird allgemein als Zentralkörper bezeichnet und ist z.B. die Sonne oder ein anderer Stern, das leichtere ist dann ein Planet, Zwergplanet, Kleinplanet oder Komet.

Man kann auch einen Planeten als Zentralkörper auffassen und dann einen Satelliten (Mond) um ihn laufen lassen. Dazu muss allerdings das gegenseitige Schwerefeld "unendlich mal" stärker sein als die Inhomogenität des Feldes zwischen Stern und Plasnet. Außerhalb der Hill-Sphäre ist das so wenig erfüllt, dass der Satellit nicht nur eine komplizierte Bahn durchläuft (wie unser Mond), sondern seinem Planeten davonläuft)

Ist das Massenverhältnis weniger extrem (bis hin zum symmetrischen Doppelsternsystem), kann man die gleichen Rechnungen auch auf das Zweikörperproblem ausweiten: ein Planet um einen Stern, aber ohne Störung anderer Objekte. Auch dann gibt es als Bahnkurven nur Kegelschnitte, nämlich die geschlossene Ellipse (incl. Kreis) und die unendlichen Formen: Parabel und Hyperbel-Ast.

Kepler hat diese Ellipse beschrieben und die bekannten drei Gesetze (1610 und 1619) formuliert, Newton hat sie dann mit seibnem Gravitationsgesetz (F = m M G/r²) erklärt: F als zentral gerichtete Anziehungskraft a ntiparallel zum Abstandsvektor der Länge r und zu einer universellen Konstante G.

Die Bahnen sind eben und haben einen konstanten Drehimpuls, wenn man das Bezugssystem passend orientiert, hängen sie nur noch vom Ort und der Geschwindigkeit im Perihel ab. Man kann sie also durch einen einzigen Punkt im Phasenraum wählen. Gleichwertig damit ist die Wahl eines anderen Punktes, den unser Programm verwendet:

Trägt man die zu einander rechtwinkligen Geschwindigkeitskomponenten v_x und v_y in einem symbolischen Raum auf, so gehören zu allen Kegelschnittformen im Ortsraum in diesem Kreise bzw. Kreisbögen, die aber nur im speziellen Fall der Kreisbahn konzentrisch zum Nullpunkt sind, ansonsten aber exzentrisch. Radius und eine Mittelpunktskoordinate können im Impulsraum (wegen konstanter Masse m praktisch der Geschwindigkeitsraum) durch einen einzigen Punkt festgelegt werden, im Programm durch einen Mausklick im Diagramm.

Zur Herleitung der Kreise im Impulsraum und der Kegelschnitte im Ortsraum vgl. den Abschnitt ganz am Ende!

Die Orientierung der Bilder setzt voraus, dass das Perihel stets rechts vom Zentralkörper ist und genau nach oben durchlaufen wird.

Dieses Bild zeigt sozusagen den Normalfall: einen Planeten, links oben im (x-y-)Ortsraum. Er bewegt sich vom Perihel (P) nach oben und erreicht sein Aphel auf dem negativen Ast der x-Achse. Die Bahn ist eine (Kepler-) Ellipse mit Mittelpunkt M und den Hauptscheiteln P (Perihel) und A (Aphel, peri = bei, apo = weit, helios = Sonne).

Für ihre Haupt- und Nebenscheitelpunkte sind die Geschwindigkeitspfeile und die Krümmungskreise (Radien: b²/a bzw. a²/b) eingetragen. Die weit gepunkteten Linien zeigen die (rechtwinkligen) Dreiecke aus Nebenscheiteln, Brennpunkten und Mittelpunkt, aus denen man die Beziehung a² = b² + e² zwischen großer und kleiner Halbabchse a und b und der "linearen Exzentrizität" e (Abstand je eines Brennpunktes vom Mittelpunkt) ablesen kann. Die beiden Brennpunkte sind einerseits die Mitte des Zentralkörpers (unser Koordinaten-Nullpunkt) und zum anderen das punctum aequans Ä, von dem aus die Winkelgeschwindigkeiten in den Apsiden (d.h. in Perihel und Aphel) gleich sind, und näherungsweise auch für den gesamten Umlauf, jedenfalls bei einigermaßen kreisnahen Ellipsen.

Die Geschwindigkeit ist im Perihel am größten. Der zugehörige Pfeil ragt in diesem Fall oben aus dem Bild heraus.

Die hellen und dunklen Ringe zeigen die Tiefe des Gravitationspotenzials (d.h. Gravitationsenergie pro Planetenmasse am jeweiligen Ort) der Sonne (allg. des Zentralkörpers) an, jede Streifenbreite bedeutet dabei einen gleich großen Schritt, ganz innen würde die Bildauflösung überschritten, dort sind darum keine Streifen eingezeichnet. Anschaulich kann man sich den Topf wie einen Trichter mit hyperbelförmigem Profil vorstellen, der in Achsenrichtung in gleich breiten Streifen bemalt ist, die aber dann in axialer Sicht als verschieden breite Ringe erscheinen. Das Schwerefeld ist um so stärker (Falllbeschleunigung!), je enger diese Streifen sind.

Rechts oben ist der Impulsraum zu sehen, wegen fester Planetenmasse ist das bios auf die Bezifferung das gleiche wie der Geschwindigkeitsraum. Der Kepler-Ellipse entspricht hier ein geschlossener Kreis, der den Nullpunkt umschließt, im allgemeinen exzentrisch, nur im Fall der Kreisbahn konzentrisch. Sein Radius entspricht dem Mittelwert der Beträge der Perihel- und der Aphel-Geschwindigkeit, sein Mittelpunkt dem Mittelwert der beiden Geschwindigkeitsvektoren, er ist proportional zum Kehrwert des Drehimpulses.

Bei der vereinbarten Orientierung der Koordinatenachsen ist der Kreis eindeutig durch die Wahl eines Punktes im Impulsraum eindeutig bestimmt, und damit auch die Bahn des Planeten, im Programm geschieht das durch die Nasenspitze der Maus und die linke Maustaste. Dabei genügt ein Quadrant des Impulsraumes (hier der rechte obere) für alle Bahnen, die im Ortsraum ihr Perihel auf dem rechten Ast der x-Achse haben, auch fürt >Parabeln und Hyperbeln. Allerdings ist bei der Eingabe ein Streifen mit kleinen v_x-Werten ausgeschlossen, weil dann im Ortsraum sehr große und im Grenzfall unendliche Werte zu zeichnen wären.

Die Steigung der Geraden vom Nullpunkt durch den rechten Scheitel des Kreises (also die Nasenspitze) zeigt die relative Exzentrizität e/a an. Diese ist 0 für die Kreisbahn, 1 für die Parabel und dazwischen für die Ellipse und darüber für die Hyperbel, im speziellen Fall ist sie 0,87.

Rechts unten ist der Potenzialtopf zu sehen, die x-Achse des Ortraumes wird direkt als Radiuskoordinate übernommen, vertikal ist die Gravitations-Energie, geteilt durch die Planetenmasse, also das Potenzial aufgetragen, die Streifen entsprechen denen im Ortsraum, auch angedeutet durch gepunktete Vertikalen. Der konventionelle Nullpunkt ist das Potenzial für unendlichen Abstand zwischen Planet und Zentralstern, also das tatsächliche Maximum. Addiert man die Bewegungsenergie des Planeten, bekommt man für Ellipsen (und Kreise, also endliche Bahnen, gebundener Lauf) kleinere Werte und für Hyperbeln größere, den Grenzfall bildet die Parabel.

Die rote Kurve ist wie die Potenzialkurve eine Hyperbel, aber nur genau "halb so tief". Auf jeweis einem Punkt auf ihr befindet sich ein Planet mit potenzieller + kinetischer Energie auf einer Kreisbahn. Bei der Ellipse pendelt er auf einer Waagerechten genau durch einen solchen Punkt mit den Abständen a-e für das Perihel und a+e f+r das Aphel, also a als Mittelpunkt.

Links unten befindet sich ein doppelt-logarithmisches Diagramm für das 3. Gesetz Keplers, demzufolge die 3. Potenz der großen Halbachse a für alle Planeten um den gleichen Zentralstern proportional zum Quadrat der Umlaufzeit ist (wenn die Masse des Planeten klein gegen die des Sterns ist und keine Störungen von dritter Seite auftreten).

Alle bisher beschriebenen Einzelheiten ergeben sich aus dem einzigen Punkt im Impulsraum, der mit der Maus ausgewählt worden ist, und den Gesetzen der Punktmechanik mitsamt Newtons Gravitationsgesetz und gewissen theoretischen Zusammenhängen. Auch die Lage des Perihels und den zugehörigen Vektor einer "Anfangs-" Geschwindigkeit hat das Programm dabei ermittelt.

Im Simulationsmodus (mit Taste s gestartet) geht es von diesen Startwerten aus und benutzt nichts anderes als das Gravitationsgesetz und ein vorgegebenes Zeitraster. Es zeigt dann in allen drei Hauptbildern eine weiße Kreisscheibe, die (sprunghaft) wandert und im Ortsraum zusätzlich jeweils mit dem Nullpunkt (Zentralstern) verbunden wird. Die Flächenstücke dazwischen sind dann nach Keplers 2. Gesetz gleich groß, wie mit Augenmaß bestätigt werden kann.

Hier sehen wir mehrere Ellipsenbahnen mit gleicher Aphelgeschwindigkeit. Die mit der größten Energie ist im Potenzialtopf die oberste und im Ortsraum die äußerste, im Impulsraum aber die innerste, ihre mittlere Bewegungsenergie ist nämlich kleiner als bei den (vom Stern aus gesehenen auch wörtlich:) höheren Bahnen.

Exkurs über elektronisch angeregte Atome: im Bohr-Sommerfeld-Modell verhalten sich Elektronen um Kerne oder um Atomrümpfe so wie Planeten um Sterne. Auch wenn man wegen der Unschärfe die Bahnformen nicht ernst nehmen darf, bleiben dabei die Mittelwerte der Kehrwerte der Abstände und damit die mittleren potenziellen Energie korrekt und ebenso die Mittelwerte der Bewegungsenergien. Wird nun ein Atom auf ein höheres Energieniveau "angeregt", indem ein Elektron nach außen springt, verliert dieses etwas Bewegungsenergie, aber das Coulomb-Feld gewinnt doppelt so viel. So kann ein H-Atom im einfachsten Fall rund 10 eV (genauer: 3/4 von 13,6 eV) aufnehmen. Dabei nimmt das Feld 20 eV auf, im Wesentlichen durch räumliche Vergrößerung, und das Elektron wird um 10 eV "langsamer". Das ganze Atom hat nun 10 eV mehr, das Elektron nur bei der üblichen, aber doch fragwürdigen Zuordnung der elektrischen Energie als potenzielle Energie "des Elektrons".

Hier sind mehrere Kreisbahnen zusammengestellt, zu jeder gehört im Topfbild nur ein einzelner Punkt auf der roten Hyperbel, zum höchsten gehört der größte Kreis im Ortsraum und der kleinste der zum Nullpunkt konzentrischen im Impulsraum.

Hier berührt der Kreis im Impulsrum den Nullpunkt, die Aphelgeschwindigigkez ist also 0. Der Planet kommt also seit unendlich langer Zeit genau von links, aber sehr langsam und wird dann schneller, rast mit maximaler Geschwindigkeit genau nach oben durch das Perihel, wird dann wieder langsamer und erreicht nach unendlicher Zeit eine genau nach linke gerichtete Geschwindigkeit mit verschwindendem Betrag. Im Ortsraum ist das eine Parabel, die also in ihrer "vollen Länge" eine Umkehrung um genau(!) 180^o vollführt. Einer gezeichneten oder als Schablone geschnittenen Parabel sieht man das nicht so ohne weiteres an.

Hat diese Parabel etwas mit der Wurfparabel im homogenen Schwerefeld zu tun? Ein solches Feld kann ja nur deshalb als homogen behandelt werden, weil man sich mit einem sehr kleinen Ausschnitt des Raumes begnügt. Tatsächlich ist die Wurfparabel die nahe Umgebung des Aphels einer Ellipse, deren Perihel sehr nahe "unter" dem Erdmittelpunkt liegt. Um den erd-inneren Teil der Bahn zu realisieren, müsste man das Erd-Innere nicht nur durchlässig für Projektile machen, sondern seine ganze Masse in eine isotrope Kugel konzentrieren, deren Radius kleiner als der Perihelabstand wäre. Für den Verlauf der Bahn außerhalb der Erde spielt das keine Rolle, wenn die Erde nur hinreichend genau isotrop ist, also eine richtungsunabhängige Massenverteilung hat: schon die Abplattung stört hier etwas.

Tatsächlich sind im Planetensystem die Perihelbereiche sehr schlanker Ellipsen nur schwer von Parabeln zu unterscheiden. Hält man einen Brennpunkt und den diesem zugewandten Scheitel einer Ellipse fest, so kann man die Parabel als Grenzfall bekommen, wenn man den anderen Brennpunkt und den anderen Scheitel unendlich weit wegwandern lässt. e/a nähert sich dann (von unten) der Zahl 1, und die Ellipse behält zwar in der Nähe des ersten Scheitels ihre Gestalt, wird aber immer länger und relativ schmaler.

Hier ist eine Schar von Parabelbahnen. Die innerste ist die "schnellste", aber alle haben an jede Stelle die Bewegungsenergie, mit der das Schwerefeld in dem Sinne verlassen können, dass sie in unendlicher Entfernung auf 0 abgebremst wären. Man kann sich das so vorstellen, dass in einem riesigen Raum, in dem nur ein einziger Stern ein Schwerefeld hat, viele nahezu ruhende Planeten ziellos aus unendlichen Entfernungen ihre Eanderschaft beginnen. Ihre Drehimpulse sind dann zufällig verschieden und bestimmen die verschiedenen Perihelabstände.

Der Radius des Scheitelkrümmungskreises ist bei der Parabel genau doppelt so groß wie der Perihelabstand.

Übrigens kann man im Impulsraum viel deutlicher als im Orstraum mit bloßen Auge sehen, ob eine Bahn eine Ellipse oder eine Parabel ist, nämlich ob der Kreis den Nullpunkt durchläuft oder umrundet.

Keplers 2. Gesetz ("Flächensatz") gilt nicht nur für Ellipsen- sondern auch für die unendlichen Parabel- und Hyperbelbahnen. Bei der Simulation beginnt unser Programm im Nahbereich und kehrt "weit draußen" die Orientierung der Zeitintervalle um:

Für Gesamtenergien/Planetenmasse oberhalb des Potenzials im Unendlichen, also "positive" Energien ist die Bahn wie bei der Parabel unendlich weit ausgedehnt, und zwar ist sie einer der beiden "Äste" einer Hyperbel, die ihrerseits durch ihre Scheitelpunkte (einer davon ist das Perihel) und zwei sich im Mittelpunkt schneidenden Asymptoten, also Grenzgeraden, bestimmt ist. Sind die Koordinaten der Scheitelpunkte (-a;0) und (+a;0) und die Steigungen der Asymptoten +b/a und -b/a, so findet man bei (-e;0) und (+e;0) mit e² = a² + b² die beiden Brennpunkte, von denen der eine (hier linke) der Ort des Zentralkörpers ist.

Im Impulsraum liegt der Kreis außerhalb des Nullpunktes, und die beiden Tangenten von diesem aus an ihn haben die gleichen Steigungen und Winkel wie die Asymptoten im Ortsraum, sie geben die Bahnrichtungungen im Unendlichen an, und die Berührpunkte selbst (durch Quadrate markiert) die asymptotischen Geschwindigkeiten unendlich lange vor und nach dem Durchlaufen des Perihels. Sie teilen den Kreis in einen größeren (im Bild oberen) Bogen durch das Perihel, der in unendlicher Zeit ganz durchlaufen wird, und einen kürzeren (nach unten), der die Kreisfigur komplettiert und nicht "benutzt" wird.

Exkurs über Rutherford-StreuungGibt es statt des anziehenden Schwerefeldes ein abstoßendes wie bei der Rutherford-Streuung mit der gleichen radialen Abhängigkeit der Stärke, so vertauschen die beiden Bögen ihre Rollen: dabei wird dann nur der kürzere Bogen durchlaufen.

Hier sind verschiedene Bahnen (Kreis, Ellipse, Parabel, Hyperbeln) mit gleichem Drehimpuls zusammengestellt:

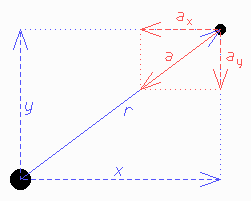
Theorie (nach Sommerfeld, Theoretische Physik I

Der Drehimpuls der laufenden Punktmasse bezüglich des Orts-Nullpunktes ist L = m r² und bleibt konstant, weil die Kraft stets dorthin gerichtet ist (Keplers 2. Gesetz), auch wenn r und einzeln nicht gleich bleiben.

Um die Schwerkraft (für das Kepler-Problem) und die Coulomb-Kraft (für das Bohr-Sommerfeld-Modell des H-Atoms) rechnerisch unter einen Hut zu bekommen, führen wir eine Konstante K ein, die bei Abstoßung positiv und bei Anziehung negativ ist. Für die Gravitation zwischen den Massen m und M ist sie K = - m M G mit der universellen Gravitations-Feldkonstanten G, für die Coulomb-Kraft zwischen den Punktladungen q und Q im Vakuum ist K = q Q/(4

₀). Die auf das Teilchen mit der Masse m wirkende Beschleunigung hat nun die Komponenten

dv_x/dt = (K/m) cos()/r² und dv_y/dt = (K/m) sin()/r².

Einsetzen von r² aus der ersten Beziehung gibt:

dv_x/dt = (K/L) cos()d/dt und dv_y/dt = (K/L) sin()d/dt

Dieses sind wegen der Kettenregel offensichtlich Ableitungen von

v_x = (K/L) sin() + C₁ und v_y = -(K/L) cos() + C₂

Das ist die Parameterdarstellung eines (sozusagen symbolischen) Kreises mit dem (also zum Drehimpuls umgekehrt proportionalen!) Radius -K/L im Geschwindigkeitsraum mit dem Mittelpunkt (C₁,C₂), der also einen Geschwindigkeitsvektor darstellt und keineswegs verschwinden muss. Wir drehen das Koordinatensystem nun so, dass C₁ verschwindet und nennen nun C₂ einfachnur noch C.

Die Transformation x = r cos(), y = r sin() zwischen cartesischen und polaren Koordinaten liefert die Geschwindigkeiten

v_x = (K/L) sin() = dx/dt = dr/dt cos() - r (d/dt) sin() und

v_y = -C - (K/L) cos() = dy/dt = dr/dt sin() + r (d/dt) cos().

Um dr/dt zu eliminieren, multiplizieren wir die obere Zeile mit -sin() und die untere mit cos() und addieren dann beide:

-C cos() - K/L = r d/dt

Wegen des (infolge der Zentralkraft) konstanten Drehimpulses L = m r² d/dt ist das

r = L/(m K/L - m C cos()),

also ein Kegelschnitt mit dem Kraftzentrum (Nullpunkt des Ortsraums) als (einem) Brennpunkt.

Falls C kleiner als K/L ist, handelt es sich im Ortsraum um eine (Kepler-) Ellipse (und speziell für C = 0 um einen Kreis). Im Geschwindigkeitsraum hatten wir bereits gesehen, dass der dortige Kreis den Radius K/L und den Abstand C des Mittelpunktes vom Nullpunkt hat, in diesem Falle also den Nullpunkt umschließt, und dass dann alle Winkel vorkommen (notwendig, aber nicht hinreichend für geschlossene Bahn; dass die Bahn tatsächlich geschlossen ist, folgt aus der Periodizität des cos).

Entsprechend sind auch die Zusammenhänge zwischen Orts- und Geschwindigkeitsraum für die Hyperbel und den Grenzfall Parabel.

Zur Simulation benötigt man eine Wiederholungs-Schleife, die etwa Folgendes enthält:

      r:=sqrt(x*x+y*y);
      KinEnergie:=(vx*vx+vy*vy)*m/2;
      PotEnergie:=-G*m*M0/r;
      GesEnergie:=KinEnergie+PotEnergie;
      ax:=-x/r*G*M0/r/r;   ay:=-y/r*G*M0/r/r;
      vx:=vx+ax*dt;        vy:=vy+ay*dt;
      x := x+vx*dt;          y := y+vy*dt;

Zur Begründung betrachten Sie bitte die einander ähnlichen Dreiecke in diesem Bild: