ESSAY

Walter Littke

Röntgenstrukturanalyse

Röntgenstrukturanalyse, Röntgenkristallographie oder Röntgenometrie ist ein Verfahren zur Aufklärung der Anordnung der Atome in Kristallen (Kristallstrukturanalyse) mit Hilfe von Röntgenstrahlen. Die ursprünglich an einfachen Kristallen entwickelte Methode konnte im Laufe der letzten 50–60 Jahre besonders erfolgreich zur Analyse der hochkomplizierten räumlichen Strukturen (Konformation, Struktur-Funktion-Beziehung, Strukturvorhersage) von Proteinen und Nucleinsäuren eingesetzt werden, so daß heute die Kenntnis der Sekundärstruktur und Tertiärstruktur praktisch aller biologisch bedeutsamen Makromoleküle (Biopolymere; Desoxyribonucleinsäuren, Ribonucleinsäuren, RNA-Topologie, Ribosomen, transfer-RNA, Lysozym, Hämoglobin, Insulin, Myoglobin, Membran, Reaktionszentren) weitgehend auf Röntgenstrukturanalyse beruht.
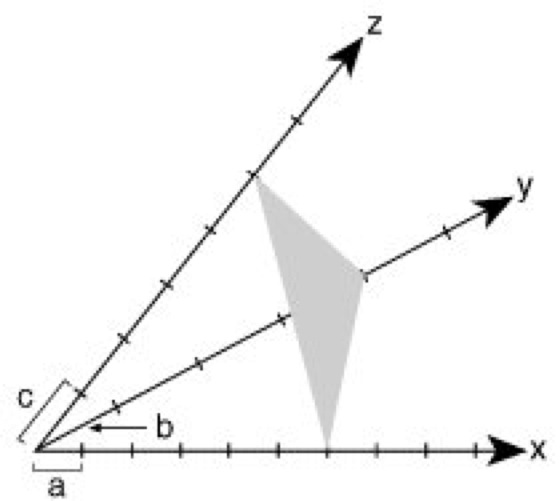
Materie im festen Aggregatzustand ist meist kristallin: die einen Kristall aufbauenden kleinsten Teilchen (Atome, Ionen oder Moleküle) sind dreidimensional periodisch translatorisch in einem starren, als Kristallgitter bezeichneten Netzwerk eingebunden ( ö vgl. Abb. 1 ). Im Gegensatz dazu bezeichnet man Festkörper mit einer regellosen, statistischen Verteilung ihrer Bausteine über große Entfernungen hinweg als armorph. Röntgenstrukturanalyse kann nur mit Kristallen ausgeführt werden (Proteinkristallisation). Ein idealer Kristall ist aus sog. Elementarzellen aufgebaut, wobei eine Elementarzelle ein von 3 möglichst kurzen, nicht komplanaren Vektoren a, b und c (vektorielle Größen sind im folgenden im Fettdruck wiedergegeben) aufgespanntes Parallelepiped (in Abb. 1 durch kräftige Linien hervorgehoben) darstellt. Je nach Länge der Vektoren (a, b, c) und nach Größe der 3 intervektoriellen Winkel α, β und γ lassen sich 7 mögliche Kristallsysteme ableiten (nach zunehmender Symmetrie: triklin, monoklin, orthorhombisch, tetragonal, trigonal, hexagonal und kubisch). Jede der 7 verschiedenen Elementarzellen ist durch die 6 Gitterkonstanten (a, b, c, α, β und γ) charakterisiert. Außerdem unterscheidet man Elementarzellen, bei denen nicht nur die 8 Ecken, wie in Abb. 1 gezeigt, sondern auch Flächenmitten oder Raumzentren der Zellen mit je 1 Teilchen besetzt sind. Dies führt in Kombination mit den 7 Kristallsystemen zu den 14 möglichen Bravais-Gittertypen. Durch ein räumliches Gitter lassen sich beliebig viele Netzebenen legen, welche mit Gitterpunkten besetzt sind ( ö vgl. Abb. 3 ). Solche Flächen schneiden auf den Achsen x, y und z des kristallographischen Koordinatensystems Abschnitte ab, welche in rationalen Zahlenverhältnissen zueinander stehen. In einem Achsensystem, das durch 3 linear unabhängige Vektoren a, b, c gegeben ist, wird eine Ebene durch ihre Schnittpunkte A, B und C mit den 3 Achsen festgelegt ( ö vgl. Abb. 2 ). Die einzelnen Achsenabschnitte sind ganzzahlige Vielfache der Einheitslängen a, b und c, also u·a, v·b und w·c. Bezogen auf Abb. 2 wäre u = 6, v = 4 und w = 5. Die Ebenengleichung

definiert alle Punkte der Ebene mit den Koordinaten x, y, z. Man bezeichnet die reziproken Maßzahlen h = 1/u, k = 1/v, l = 1/w als die Indizes der Fläche. Im Falle von Abb. 2 wäre





Die gemeinsame Multiplikation mit dem gemeinschaftlichen Vielfachen der Nenner (60 im obigen Fall) ändert nichts an ihrem Verhältnis, so daß auch das Indextripel h : k : l ganzzahlig bleibt:





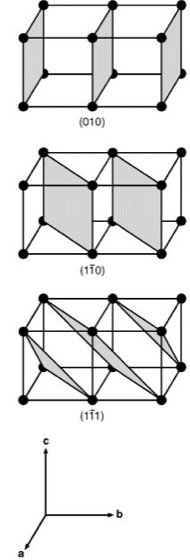
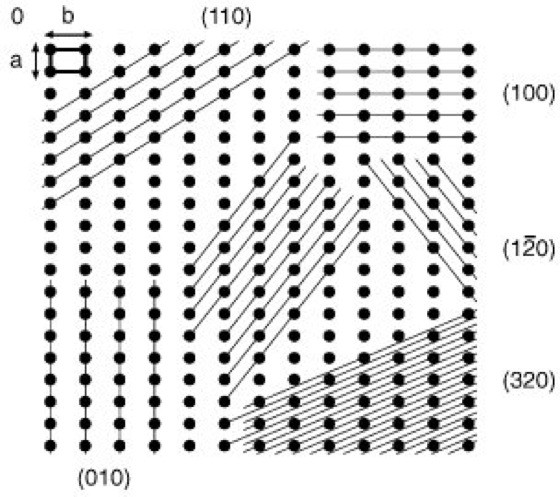
In dieser Form bezeichnet man das Indextripel (h k l ) = (hier 10, 15, 12) als Millersche Indizes der betreffenden Kristallfläche. Jede Netzebene läßt sich also durch die Millerschen Indizes definieren. Der besseren Anschaulichkeit wegen sind in Abb. 3 verschiedene Netzebenenscharen mit den zugehörigen Miller-Indizes dargestellt. Den kürzesten Abstand d von Netzebene zu Netzebene bezeichnet man als Identitätsperiode. Dreidimensionale Beispiele sind in Abb. 4 dargestellt ( ö vgl. Abb. 4 ). – Zu den Wesensmerkmalen des Kristallaufbaus gehören ganz charakteristische Symmetrieeigenschaften. Symmetrie ist die regelmäßige Wiederholung eines Ausschnitts der Kristallstruktur. Geometrische Operationen, die solche Wiederholungen erzeugen, werden Symmetrieoperationen oder Deckoperationen genannt. Solche Deckoperationen lassen sich durch Drehung um eine Achse (2-, 3-, 4- oder 6zählige Drehachse) oder durch Spiegelung an einem Punkt (Inversionszentrum) oder an einer Spiegelebene erzeugen. Aus diesen Elementen oder deren Kombination lassen sich unter Berücksichtigung der 7 Kristallsysteme 32 Punktgruppen (Kristallklassen) ableiten. Die Kopplung einer Drehung mit einer Translation ergibt eine Schraubung, die Kopplung einer Spiegelung mit einer Translation eine Gleitspiegelung. Die zugehörigen Symmetrieelemente werden als Schraubenachse bzw. als Gleitspiegelebene bezeichnet. Unter Berücksichtigung aller möglichen Symmetrieoperationen resultieren 230 verschiedene Raumgruppen. – Kristallgitter streuen, wie alle Gitter, Licht (Streuung). Für solche Streuexperimente ist erforderlich, daß die Wellenlänge (Welle) des Lichts mit den Teilchenabständen des Gitters ungefähr kommensurabel ist. Die Größenordnung liegt bei Kristallgittern im Bereich von Ångström (1 Ångström = 1 Å = 0,1 nm = 10^–8 cm). Deshalb wird für Strukturaufklärungen überwiegend Röntgenstrahlung (Wellenlängen: Cu K

= 1,541838 Å oder Mo K

= 0,71073 Å) verwendet. In zunehmendem Maße wird heute auch Röntgenstrahlung eingesetzt, die mittels Synchrotrons (Teilchenbeschleuniger) erzeugt werden. Diese Synchrotronstrahlung besitzt eine höhere Intensität und kann in Wellenlängen gewählt werden, die sich z.B. von Kupfer-K

unterscheiden. Die Streuung erfolgt an den Elektronen der im Gitter befindlichen Atome. Je höher die Elektronenanzahl pro Element (entsprechend der Ordnungszahl, d.h. Protonenzahl), desto stärker ist die Streukraft. Gelegentlich verwendet man für Streuexperimente auch Neutronenstrahlung (Neutronenbeugungsuntersuchungen). Neutronen werden im Gegensatz zur Röntgenstrahlung nicht durch die Elektronen, sondern durch die Kerne der anwesenden Atome gestreut. – Abb. 5 zeigt das Prinzip der Dunkelfeldmikroskopie. Ein zu untersuchendes Objekt O streut das einfallende Primärlicht P (sichtbares Licht der Wellenlänge 380 nm = 3800 Å bis ca. 760 nm = 7600 Å). Das Streulicht S wird auf eine optische Sammellinse L geleitet und erzeugt dort ein Beugungsmuster (Beugung). Das komplizierte Beugungsbild, aus dem das Bild des Objekts O nicht direkt erkannt werden kann, wird durch die Linse wieder zum erkennbaren Bild B rückverwandelt, welches seinerseits mit Lupen (Okularen) betrachtet und vergrößert werden kann. Der nicht-gestreute Anteil des Primärstrahls P läßt sich durch den Primärstrahlfänger F unterdrücken. Röntgenmikroskope gemäß dieser Anordnung sind prinzipiell nicht möglich, da es für „Röntgenlicht“ keine optischen Sammellinsen gibt. Deshalb ersetzt man bei Röntgenstreuexperimenten an Kristallen die Linse L durch einen photographischen Film ( ö vgl. Abb. 6 ) und registriert das Beugungsbild, auch Eigendiagramm genannt ( ö vgl. Infobox ). Ein typisches Röntgendiagramm (Präzessionstechnik) ist in Abb. 7 wiedergegeben. Es besteht aus Punkten definierter Lage, wobei die einzelnen Punkte, auch Reflexe genannt, verschiedene Intensitäten aufweisen. Jeder einzelne Reflex ist das Abbild einer bestimmten Netzebene des Kristallgitters und läßt sich durch die entsprechenden Miller-Indizes charakterisieren. Aus der gegenseitigen Lage der Reflexe können die Gitterkonstanten berechnet und die Kristallsymmetrie bestimmt werden. Die eigentliche Kristallstruktur, d.h. die Lage aller Atome innerhalb der Elementarzelle, läßt sich aus den Intensitäten der Reflexe berechnen. Dies erfolgt durch Fourier-Synthese, eine relativ aufwendige mathematische Prozedur. Der Weg AV ( ö vgl. Abb. 5 ) vom Eigendiagramm zum Bild entspricht einer Fourier-Synthese, welche im Falle sichtbaren Lichts durch die Linse L gelöst wird. Im Gegensatz dazu läßt sich Röntgenstrahlung nicht durch herkömmliche Linsen beeinflussen. Der Aufbau eines Röntgenmikroskops ist deshalb, wie bereits erwähnt, nicht möglich. In diesem Falle, d.h. bei Röntgenstrukturanalysen, muß der Rückweg AR ausschließlich mathematisch durch Fourier-Synthese bewerkstelligt werden. Aus dem Eigendiagramm ( ö vgl. Abb. 7 ) ist zu entnehmen, daß Reflexe nur an definierten Stellen entstehen. Formell kann die Röntgenstreuung als Reflexion des Strahls an beliebigen Netzebenen nach der Braggschen Gleichung sin Θ = n·λ/(2d) aufgefaßt werden. Der Reflexionswinkel Θ ist abhängig von der Wellenlänge λ des einfallenden Röntgenstrahls sowie von der Identitätsperiode d (kürzester Abstand von 2 streuenden, parallel liegenden Netzebenen) und von der Ordnung n des betreffenden Reflexes. Auf diese Weise kommen die punktförmigen Reflexe zustande. – Die Elektronendichte ρ (Orbital [Abb.]), d.h. die Position von Atomen in der Elementarzelle, läßt sich durch das Fourier-Integral beschreiben:

(1)




Bezogen auf die Elementarzelle in Abb. 8 bedeutet dies, daß die Elektronendichte ρ an jedem beliebigen Punkt (Koordinaten x, y, z) der Zelle berechnet werden kann, sofern das Zellvolumen V sowie die Strukturamplituden F nebst zugehörigen Phasen α (s.u.) und Miller-Indizes h, k, l der einzelnen Reflexe bekannt sind ( ö vgl. Abb. 8 ). Die Integration (Summation) läuft über alle h, alle k und alle l der Miller-Indizes vorhandener Reflexe. Wenn alle genannten Größen bekannt wären, könnte man die Lösung einem Computer anvertrauen: je nach gewünschter Genauigkeit müßten Tausende oder Millionen Punkte x, y, z der gesamten Elementarzelle abgerastert und an jedem einzelnen Punkt die jeweilige Elektronendichte ρ berechnet werden, so wie es schematisch für den Punkt E in Abb. 8 dargestellt ist. Eine Röntgenstrukturanalyse, d.h. die Rückrechnung vom Beugungsbild in den Objektraum, würde sich somit zu einer raschen und einfachen Routinetätigkeit gestalten. Dies wird jedoch durch das „Phasenproblem“ verhindert: Die Phase α jedes einzelnen Reflexes geht bei der physikalischen Messung verloren und muß über andere Wege bestimmt werden. Das Zellvolumen V läßt sich aus den 6 Gitterkonstanten a, b, c, α, β, γ, welche ihrerseits aus der geometrischen Lage der Reflexe zueinander bestimmt werden können, berechnen. Die Strukturamplitude |F|_hkl jedes einzelnen Reflexes mit den Miller-Indizes h k l ist einfach aus der Intensität I (Filmschwärzung) jedes einzelnen Reflexes über die Beziehung

(2) 



zu ermitteln, wobei k eine Skalierungskonstante darstellt. Zur Berechnung der Elektronendichten ρ ist die alleinige Kenntnis der Strukturamplituden |F|_hkl der einzelnen Reflexe nicht ausreichend. Es muß auch die jeweilige Phase α_hkl bekannt sein. Strukturamplitude und Phase eines Reflexes liefern dessen StrukturfaktorF

(3) 



Ein Strukturfaktor kann, wie aus Abb. 9a ersichtlich, als Vektor F in der sog. Gaußschen Zahlenebene (Abszisse = Realachse, Ordinate = Imaginärachse, i = √-1) dargestellt werden ( ö vgl. Abb. 9 ). Seine Lage ist durch die Phase α, seine Länge durch die Strukturamplitude |F| festgelegt. Je stärker die Intensität eines Reflexes, desto größer ist der Radius des Kreises. Für Strukturen, die azentrischen Raumgruppen zuzuordnen sind, ist 0° ≤ α ≤ 360°. Bei den zentrosymmetrischen Raumgruppen gibt es dagegen nur 2 Möglichkeiten: α = 0° oder α = 180° (Abb. 9b). Abb. 10 zeigt den Zusammenhang zwischen vektorieller (10a) und trigonometrischer (10b) Darstellung des Strukturfaktors. Eine einfache harmonische Welle (Fourier-Analyse) kann durch einen Punkt A ( ö vgl. Abb. 10a ), welcher sich auf einer Kreisbahn mit konstanter Winkelgeschwindigkeit bewegt, dargestellt werden. Die Projektion auf die Realachse (Abszisse) bewirkt dadurch eine einfache harmonische Schwingung des Punktes B. Die lineare Bewegung von B als Funktion der Winkeländerung α des Radiusvektors (Strukturfaktor) führt zu einer Cosinusfunktion ( ö vgl. Abb. 10b ). Die numerische Beziehung ist durch den Satz nach Euler

(4) 



festgelegt. Jeder einzelne Reflex enthält durch seine individuelle Intensität die Aussage über sämtliche Atompositionen innerhalb der Elementarzelle. Jedes Atom hat eine festgelegte Streukraft. Sie läßt sich ebenfalls vektoriell, analog dem Strukturfaktor, in der Gaußschen Zahlenebene dastellen und wird als Atomformfaktorf bezeichnet. Seinen skalaren Wert, d.h. die Länge des Vektors, nennt man Atomformamplitude |f|. Die Vektoraddition sämtlicher Atomformfaktoren, d.h. die Summation der Streukräfte der Atome j der Elementarzelle, führt zum Strukturfaktor F:

(5) 



Der Strukturfaktor bezieht sich auf einen Reflex, d.h. auf eine Netzebene mit den Miller-Indizes h k l. – Für eine Strukturaufklärung reicht die in einem einzelnen Reflex enthaltene Aussage nicht aus. Es ist erforderlich, die Intensitäten (Strukturamplituden) einiger hundert oder tausend Reflexe zu messen. Je höher die Anzahl an Atomen in der Elementarzelle, desto mehr Intensitäten müssen bekannt sein, um eine ausreichende Strukturgenauigkeit zu erhalten. Während man früher solche Daten durch photometrische (Photometrie) Ausmessung jeder Punktschwärzung (Reflex) auf photographischen Filmen bestimmte, werden die Intensitäten heute mit Hilfe von computergesteuerten Diffraktometern und automatisch auslesenden Detektoren gesammelt. Die durch solche Messungen nicht zugänglichen Phasen α können durch verschiedene mathematische Methoden erhalten werden:
a) Die dreidimensionalen periodischen Atomanordnungen im Kristallgitter können durch eine periodische Funktionρ(x,y,z) (vgl. Gleichung 1) näherungsweise dargestellt werden. Wegen des Phasenproblems benutzt man modifizierte Fourier-Reihen, sog. Patterson-Reihen, bei denen die der Messung direkt zugänglichen Größen |F_hkl|² (= Intensitäten, vgl. Gleichung 2) als Koeffizienten eingehen. Die Patterson-Reihen liefern im Gegensatz zu den Fourier-Reihen zwar nicht die gesuchte Elektronendichtefunktion ρ(x,y,z), führen jedoch zu den Punktlagen der schwereren Atome in der Elementarzelle. Aus dieser Teilinformation können weitere Phasen ermittelt werden.
b) Man leitet die unbekannten Phasen α durch „Direkte Methoden“ ab. Das Verfahren erlaubt, innerhalb berechenbarer Wahrscheinlichkeiten Aussagen über die Phasen von Strukturfaktoren zu machen. Grundlage dafür bilden Reflexintensitätsstatistiken.
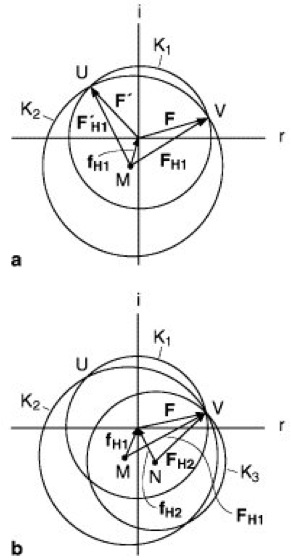
c) Der „isomorphe Ersatz“ wird speziell bei der Strukturermittlung von Proteinen angewandt. Das Verfahren ist aus den Abb. 11a und 11b zu entnehmen ( ö vgl. Abb. 11 ). Zunächst bestimmt man Strukturamplituden |F| am nativen, d.h. unbehandelten Proteinkristall. Anschließend läßt man in den Kristall Schwermetallionen oder Schwermetallverbindungen einer einzigen Schwermetallsorte H1 eindiffundieren (Diffusion). Voraussetzung dafür ist, daß die eindiffundierenden Teilchen von jedem Proteinmolekül an ein und derselben Stelle fixiert werden, d.h., die Teilchen dürfen im Kristallgitter nicht statistisch verteilt, sondern müssen streng periodisch translatorisch angeordnet vorliegen. Die Positionen des Schwermetalls innerhalb des Proteins kann durch Patterson-Synthese ermittelt und somit der Atomformfaktor f_H1 in der Gaußschen Zahlenebene festgelegt werden (Abb. 11a). Man erhält so den Mittelpunkt M des Kreises K₂. Der Kreisradius ist die Strukturamplitude |F_H1|. Für das native, d.h. schwermetallfreie Protein wird die Strukturamplitude (Radius) |F| vom Zentrum der Gaußschen Zahlenebene aus gezeichnet (Kreis K₁). Man erhält die beiden Schnittpunkte V und U und somit 2 in Frage kommende Strukturfaktormöglichkeiten, F und F':





Zwischen den beiden Möglichkeiten kann man durch ein zweites Experiment mit einem verschiedenen Schweratomderivat unterscheiden. In Analogie zum vorigen Fall erhält man den Atomformfaktor f_H2 und somit den Mittelpunkt N für den Kreis K₃. Der Radius dieses Kreises entspricht der Strukturamplitude |F_H2|. Alle 3 Kreise schneiden sich im Punkt V, d.h., der Strukturfaktor F für das native Protein ist eindeutig festgelegt. Die Möglichkeit F' scheidet aus. Auf diese Art lassen sich die Phasen α bestimmen und somit die Elektronendichtefunktionen ρ_x,y,z berechnen (Gleichung 1).
d) Eine Variante des isomorphen Ersatzes ist die anomale Dispersion, bei der die Änderung des Atomformfaktors in Abhängigkeit von der Wellenlänge des Röntgenlichts zur Phasenbestimmung benutzt wird. Die Änderung erfolgt an der sog. Absorptionskante eines Atoms und ist bei Schweratomen gut meßbar.
e) Eine Variante der unter a) genannten Patterson-Methoden ist möglich, wenn die gesuchte Proteinstruktur aus früheren Untersuchungen ungefähr bekannt ist. Die Modellstruktur läßt sich in der Patterson-Funktion auffinden und zur Phasenbestimmung nutzen.
Ganz allgemein legt man bei Fourier-Synthesen zur Vereinfachung Schnitte durch die Elementarzellen. Man erhält auf diese Weise die Elektronendichteverteilung der entsprechenden Ebene ( ö vgl. Abb. 12 ). Verbindet man Elektronendichten gleicher oder ähnlicher Größen, dann entsteht ein Bild, wie es von Landkarten (mit ihren Isolinien) her bekannt ist. Die Elektronendichtekurven entsprechen den Höhenlinien: Das Zentrum des Atoms liegt im Zentrum der jeweiligen Kurvenschar. Durch Kombination verschiedenster Schnitte durch die Elementarzelle, wobei jeder Schnitt eine Elektronendichtekarte darstellt, erhält man sämtliche Atompositionen und somit die dreidimensionale Struktur. Die Verfeinerung der Positionsberechnungen, d.h. die Schärfung der Struktur, wird meist durch Anwendung der sog. Vollmatrixmethode bewerkstelligt und stellt die Endprozedur einer Röntgenstrukturbestimmung dar. Abb. 13 zeigt die Verfeinerung der in Abb. 12 dargestellten Struktur ( ö vgl. Abb. 12 und 13 ). In diesem Fall handelt es sich um einen Schnitt durch die Molekülebene. Wasserstoffatome (Wasserstoff) lassen sich wegen der geringen Streukraft nur indirekt über Differenz-Fourier-Synthesen festlegen. – Ein Maß für die Zuverlässigkeit und die Qualität einer Strukturbestimmung ist der R-Wert, definiert durch:





d.h., man vergleicht die Absolutwerte der gemessenen Strukturamplituden |F_o| jedes einzelnen Reflexes mit den berechneten |F_c|: Je besser die Übereinstimmung, desto niedriger ist der R-Wert (Null im Idealfall – ein Wert, der jedoch aus verschiedenen Gründen nicht erreicht werden kann). Biochemie (Geschichte der), Biophysik, Brookhaven Protein Data Bank, Crick (F.H.C.), Cytologie, Deisenhofer (J.), Faserdiagramm, Franklin (R.E.), Hodgkin (D.M.), Huber (R.), Karle (J.), Kendrew (J.C.), Kernresonanzspektroskopie, Klug (A.), Michel (H.), Mikrotomographie, molecular modeling, Pauling (L.C.), Perutz (M.F.), Raster-Tunnelelektronenmikroskop, Watson (J.D.); ä Desoxyribonucleinsäuren III , Proteine II , Ribosomen .

Lit.:Borchardt-Ott, W.: Kristallographie. Eine Einführung für Naturwissenschaftler. Heidelberg ⁴1993. Drenth, J.: Principles of Protein X-ray Crystallography. New York 1994. Ducruix, A., Giege, R.: Crystallization of Nucleic Acids and Proteins. Oxford 1992. Glusker, J.P., Lewis, M., Rossi, M.: Crystal Structure Analysis for Chemists and Biologists. Weinheim 1994. Lottspeich, F., Zorbas, H. (Hrsg.): Bioanalytik. Heidelberg, Berlin 1998. Massa, W.: Kristallstrukturbestimmung. Stuttgart ²1996.

Röntgenstrukturanalyse

Abb. 1

Röntgenstrukturanalyse

Abb. 2

Röntgenstrukturanalyse

Abb. 3

Röntgenstrukturanalyse

Abb. 4

Röntgenstrukturanalyse

Abb. 5

Röntgenstrukturanalyse

Abb. 6:
1 Versuchsanordnung zur Aufnahme eines sog. Laue-Diagramms. Die im Kristallgitter in regelmäßiger Anordnung vorliegenden Atome wirken für Röntgenstrahlen wie ein dreidimensionales Beugungsgitter. Aus den auf einem Film aufgezeichneten Röntgenstrahlinterferenzen ( ö vgl. Abb. 3 unten) können die Atomabstände (Gitterkonstante) und die räumliche Atomanordnung (Tertiärstruktur) bestimmt werden. 2Röntgenbeugungsmuster eines DNA-Faserbündels, in der B-Form, nach R. Franklin und M. Wilkins (1952). Die starken Reflexe oben und unten entstehen durch eine dominierende Periode von 0,34 nm, was der Dicke aromatischer Ringsysteme entspricht. Die Kreuzfigur in der Mitte weist auf einen helikalen Aufbau hin. (Für den Durchgang des direkten, ungebeugten Röntgenstrahls wird in der Filmmitte ein Loch gestanzt.) 3 Röntgenbeugungsbild (Laue-Diagramm) eines einzelnen Hämoglobinkristalls. – Aus den Röntgenbeugungsdaten erschlossene räumliche Gestalt des Hämoglobin- und Myoglobinmoleküls: ä– Hämoglobin – Myoglobin .

Röntgenstrukturanalyse

Abb. 7

Röntgenstrukturanalyse

Abb. 8

Röntgenstrukturanalyse

Abb. 9

Röntgenstrukturanalyse

Abb. 10

Röntgenstrukturanalyse

Abb. 11

Röntgenstrukturanalyse

Abb. 12 und 13