Lexikon der Neurowissenschaft: neuronale Netze
neuronale Netze, neuronale Netzwerke, Abk. NN, Eneural networks, 1) Netze von Nervenzellen, die durch Synapsen miteinander verbunden sind (Nervennetze). 2) künstliche neuronale Netze (Abk. KNN), auf dem Rechner realisierte Simulationsmodelle von Neuronennetzen, d.h. Netze aus künstlichen Neuronen. Dabei unterscheidet man biologisch orientierte und technisch orientierte Simulationen. In den biologisch orientierten Simulationen steht die möglichst getreue Wiedergabe von neuronalen Eigenschaften im Vordergrund, die in der Neurobiologie untersucht werden (spikes, dynamische Synapsen, elektrische Signalleitung in Dendriten und Axonen). In technisch orientierten Simulationen geht es um den Einsatz künstlicher neuronaler Netze zur Lösung technischer Probleme, etwa in der Mustererkennung oder bei der Vorhersage von Zeitreihen; dies ist Gegenstand der Neuroinformatik ( siehe Abb. 1 ). – Die Konstruktion von KNN zur Lösung technischer Probleme kann als ein neues Programmierparadigma angesehen werden: Man gibt eine Netzwerkstruktur und eine sogenannte Lernregel vor, nach der sich das Netz an die zu lernende Funktion anpassen kann, und "trainiert" dann das neuronale Netz durch Beispieldaten ( siehe Tab. 1 ). Hier wird also vor allem die Adaptivität und die Lernfähigkeit von neuronalen Netzen ausgenutzt, um das "Programmieren", also die Erstellung und Modifikation von Programmen zu erleichtern. Ein weiterer technischer Aspekt, der häufig zum Einsatz von KNN führt, ist die prinzipielle Parallelisierbarkeit der Simulation von KNN. Dies liegt daran, daß in einem neuronalen Netz alle Neurone gleichzeitig arbeiten, während die meisten Algorithmen nicht ohne weiteres parallel (also von verschiedenen Prozessoren gleichzeitig) ausführbar sind. Der effektive Einsatz von Parallelrechnern wird vor allem bei zeitkritischen Anwendungen gelegentlich notwendig, aber auch bei sehr rechenintensiven Problemstellungen, z.B. beim Optimieren der neuronalen Verbindungsstruktur durch Lernen (Grundtypen technischer neuronaler Netze siehe Tab. 2 ).
Aufbau von künstlichen neuronalen Netzen: Ein KNN ist ein Netzwerk aus formalen Neuronen oder Neuronenmodellen. Es wird im wesentlichen durch drei Komponenten spezifiziert: – 1) Das Neuronenmodell beschreibt die Eingangs-Ausgangs-Beziehungen eines einzelnen Neurons. Ein Neuron hat dabei viele Eingänge und einen Ausgang. In vielen Modellen werden zunächst die Eingänge (x1,...,xn) mit Gewichten aus einem Gewichtsvektor w = (w1,...,wn) multipliziert und dann aufaddiert: ![]()
.
Daraus wird mit einer nichtlinearen Funktion f das Ausgangssignal berechnet: a = f(d). Häufig wird dabei f als Antwortcharakteristik oder Kennlinie des Neurons, a als "axonale Aktivität" und d als "dendritisches Potential" bezeichnet. Dies bezieht sich auf die entsprechende Funktion von Axon und Dendrit im biologischen Neuron. In stochastischen Neuronenmodellen spielt bei der Übertragungsfunktion f von d nach a ein Zufallsprozeß mit hinein. Dieser modelliert z.B. statistische Fluktuationen des dendritischen Membranpotentials. Bei einem besonders einfachen Neuronenmodell, dem sogenannten Schwellenneuron oder McCulloch-Pitts-Neuron, wird eine Erregungsschwelle θ vorgegeben, die von der dendritischen Aktivität d überschritten werden muß, damit das Neuron einen Output (oft als spike interpretiert) produziert (a = 1). Es ist also f(d) = fθ(d) = 1, falls d ≥ θ , und sonst ist fθ(d) = 0. Sehr häufig wird auch eine differenzierbare sigmoide Funktion f verwendet: die Fermi-Funktionf(d) = 1/(1+exp(-βd)). In diesem Fall wird der Ausgang a = f(d) als Spikerate interpretiert. – 2) Die Verknüpfungsstruktur gibt an, wie die künstlichen Neurone untereinander verbunden sind, welche Neurone entweder durch ihre Eingänge oder direkt durch ihre Ausgangsaktivität die Eingänge in das Netzwerk repräsentieren, und welche Neurone durch ihre Ausgänge die Ausgänge aus dem Netzwerk darstellen. Im einfachsten Fall kann die interne Verbindungsstruktur einfach durch eine Matrix C = (cij) beschrieben werden, wobei z.B. cij = 1 ist, falls Neuron i mit Neuron j verbunden ist, und sonst cij = 0, oder cij als reelle Zahl die Stärke der Verbindung zwischen Neuron i und Neuron j angibt. Dabei bedeuten positive Zahlen erregende Verbindungen und negative Zahlen hemmende Verbindungen. In biologischen neuronalen Netzen werden diese Verbindungen durch Synapsen hergestellt; ein chemischer Transmitter (Neurotransmitter) erzeugt dort die erregende oder hemmende Wirkung in der nachgeschalteten (d.h. postsynaptischen) Zelle. Diese Verbindungsstruktur eines Netzes kann auch gut durch einen gewichteten Graphen dargestellt werden. Dabei werden die Neurone als Knoten und die Verbindungen als Kanten des Graphen dargestellt. Im Falle asymmetrischer Verbindungen wird die Verbindungsrichtung durch einen Pfeil ausgedrückt. Die Verbindungsstärken können als Gewichtswerte an die Kanten geschrieben werden. – Zur Klassifikation der Verknüpfungsstruktur ist es wichtig, vorwärtsgekoppelte (feedforward network) und rückgekoppelte (Feedback) Netze zu unterscheiden. Bei vorwärtsgekoppelten Netzen gibt es keine geschlossenen Schleifen (Zyklen), auf denen die Aktivität eines Neurons nach einer Anzahl von Zwischenschritten wieder auf dasselbe Neuron zurückwirken kann. Besonders einfache vorwärtsgekoppelte Netze sind die mehrschichtigen Perzeptrone (E multilayer perceptrons), bei denen eine Schicht jeweils eine Menge von künstlichen Neuronen enthält. Die Neurone der ersten Schicht repräsentieren durch ihre axonale Aktivität den Eingang in das Netz, alle Neurone einer Schicht haben Verbindungen zu allen Neuronen der jeweils nächsten Schicht, und die Neurone der letzten Schicht stellen den Ausgang des Netzes dar. – 3) Die Lernregel gibt an, wie sich die Verbindungen cij oder die Gewichte wij zwischen zwei Neuronen i und j verändern (synaptische Plastizität). Bei lokalen Lernregeln hängt die Änderung Δcij von cij nur von der Aktivität in Neuron i und in Neuron j ab; außerdem kann noch ein sogenanntes LehrersignalTj für Neuron j und unter Umständen ein zusätzliches "Lernsignal" l berücksichtigt werden, welches anzeigt, ob gelernt werden soll oder nicht (Δcij = 0). Die gebräuchlichsten Lernregeln sind Produktregeln: bei ihnen ist die Änderung Δcij ein Produkt von zwei Faktoren A und B, die jeweils nur von der axonalen Aktivität ai bzw. der dendritischen Aktivität dj abhängen: Δcij = A(ai) · B(dj). Spezialfälle hiervon sind die Hebb-Lernregeln: Δcij ≈ lai · aj, und die Differenzregeln: Δcij ≈ lai · (Tj-aj), bei denen zusätzlich ein Lehrersignal benötigt wird. Der Faktor l ≥ 0 wird auch als Lernrate bezeichnet. Er gibt an, wie stark die Synapse geändert wird; bei l = 0 findet keine Veränderung statt. In vielen Modellen wird die Lernrate während des Lernens verringert; sie ist dann also zeitabhängig l = l(t) ( siehe Zusatzinfo ).
Anwendung von künstlichen neuronalen Netzen:Die heute unter den Anwendern populären Modelle sind überwiegend vorwärtsgekoppelt (d.h., es gibt in ihnen keine Rückkopplungen; siehe Tab. 3 ). Dies liegt vor allem daran, daß das Verhalten von rückgekoppelten Netzen mathematisch viel schwieriger zu analysieren und auch praktisch nicht einfach vorhersehbar ist; praktische Anwendungen liegen vor allem im Einsatz stochastischer rückgekoppelter Netze zur Optimierung (Boltzmann-Maschine, Hopfield-Netzwerk). – Das wohl bekannteste KNN, das einfache Perzeptron, ist ein einschichtiges Netzwerk aus binären Neuronen mit Inputvektor x, einer Kopplungsmatrix c und Outputvektor a. Bei den mehrschichtigen Perzeptronen hat sich heute allerdings eine andere Zählung der Schichten durchgesetzt: man repräsentiert die Inputs durch eine erste Schicht von Neuronen und bezeichnet also das einfache Perzeptron als zweischichtig, mit einer Input- und einer Outputschicht. Das erste echte Mehrschicht-Perzeptron ist dann dreischichtig, mit einer Input-, einer Output- und dazwischen einer sogenannten verborgenen (E hidden)Schicht ( siehe Abb. 2 ). Das einfache Perzeptron wurde bereits von Rosenblatt und später von Minsky und Papert (1969) ausführlich untersucht. Bei den Assoziativspeichern handelt es sich gewöhnlich ebenfalls um einschichtige Netze aus binären Neuronen mit etwas anderen Lernregeln. Bei der Optimierung der Speicherkapazität von Assoziativspeichern stellt sich heraus, daß spärliche Muster (mit wenig Einsen und überwiegend Nullen) vorzuziehen sind. Man unterscheidet hier zwischen Hetero-Assoziation und Auto-Assoziation. Im Falle der Auto-Assoziation (autoassoziatives Netz), wo der Input-Vektor mit dem Output-Vektor übereinstimmt, betrachtet man häufig rückgekoppelte Netze (z.B. Hopfield-Netze, in denen der Output-Vektor iterativ verbessert wird). – Manche Verfahren können nur im weiteren Sinne als KNN betrachtet werden, weil bei ihnen in jedem Neuron nicht das innere Produkt ![]()
aus dem Inputvektor x und den Gewichten berechnet wird, sondern die Distanz ![]()
.
Dies ist der Fall bei radialen Basisfunktionen (Abk. RBF), Kohonen-Karten, dem damit verwandten Learning vector quantisation (Abk. LVQ) und der adaptiven k-means Clusterung (eine Methode der Ballungsanalyse; Clusteranalyse). Bei den sehr populären Kohonen-Karten oder selbstorganisierenden Karten experimentiert man außerdem mit einer zeitabhängigen Lernrate l(t) und mit einer unter Umständen ebenfalls zeitabhängigen Nachbarschaft N(j,,j*) des Gewinnerneurons j*, in welcher ebenfalls gelernt wird. – Bei der Boltzmann-Maschine handelt es sich um ein rückgekoppeltes stochastisches Netz mit einem etwas komplizierten und rechenaufwendigen Lernverfahren, das durch Modelle der statistischen Mechanik motiviert ist. Ein wichtiger Parameter ist hierbei die "inverse Temperatur" β, die die Steilheit der Fermi-Funktion (s.o.) bestimmt, und die während der Simulation systematisch verändert werden muß (simulated annealing). Backpropagation ist ein Lernverfahren für mehrschichtige Netze (von Neuronen mit differenzierbarer Übertragungsfunktion), in denen Fehlersignale δi zunächst für die Ausgangsschicht berechnet werden δj = (Tj – aj) und dann schrittweise über die Kopplungsmatrizen von Schicht zu Schicht auf die davorliegenden Schichten zurückpropagiert werden (Fehlerrückmeldungsverfahren). – Bei praktischen Anwendungen von KNN ergibt sich häufig ein Problem, das man als Architekturproblem bezeichnen kann. Es besteht grundsätzlich in der optimalen Wahl derjeniger Parameter, die ein KNN spezifizieren und nicht durch das Lernverfahren angepaßt werden. Zum Beispiel muß man sich beim Einsatz mehrschichtiger Perzeptrone (mit Backpropagation-Lernverfahren) entscheiden, wieviele Schichten und wieviele Neurone pro Schicht man verwendet; d.h., man muß sich, allgemein gesagt, für eine bestimmte Architektur der Netzverschaltung entscheiden. Da das Lernverfahren viele Iterationsschritte benötigt, ist hier ein Herumprobieren mit verschiedenen Architekturen sehr zeitaufwendig.
Die Theorie von künstlichen neuronalen Netzen wurde in den 1950er Jahren zusammen mit der Automatentheorie begonnen und nach einer Pause in den 1970er Jahren in letzter Zeit wieder verstärkt vorangetrieben. Die wichtigsten Resultate sind hier abschließend kurz zusammengefaßt:
- KNN haben die gleiche Berechnungskapazität wie endliche Automaten.
- Rückgekoppelte KNN mit symmetrischen Verbindungen (cij = cji) haben stabile Fixpunkte und keine langen Zyklen (die Länge ist maximal 2). Die dynamische Entwicklung bewegt sich in Richtung minimaler Energie H. Die Funktion H des Aktivitätsvektors a = (a1,...,an) ist im wesentlichen definiert als ![]()
.
- Die Differenz-Lernregel des einfachen zweischichtigen Perzeptrons konvergiert nach endlich vielen Schritten.
- Das dreischichtige Perzeptron kann jede stetige Funktion approximieren (mit genügend vielen Neuronen in der verborgenen Schicht).
- Das Optimierungsproblem, beim dreischichtigen Perzeptron durch "Lernen" die beste Approximation an eine vorgegebene Funktion zu finden, ist schwierig.
- Das Architekturproblem, also die Frage, ob ein bestimmtes mehrschichtiges Perzeptron (mit weitgehend festgelegter Architektur) eine vorgegebene Funktion richtig (oder wenigstens approximativ richtig) darstellen kann, ist ebenfalls schwierig.
G.P.
Lit.:Cybenko, G.: Approximation by superpositions of a sigmoidal function. Math. of Control, Signals and Systems 2 (1989), S. 303-314. Hertz, J., Krogh, A., Palmer, R.G.: Introduction to the theory of neural computation. Redwood City 1991. Hopfield, J.J.: Neural networks and physical systems with emergent collective computational abilities. PNAS 79 (1982), S. 2554-2558. Kleene, S.C.: Representation of events in nerve nets and finite automata. In: Shannon, L.E., McCarthy, I. (Hrsg.): Automata studies. Princeton 1956, S. 3-41. McCulloch, W.S., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5 (1943), S. 115. Minsky, M., Papert, S.: Perceptrons. Cambridge 1969. Palm, G.: Neural assemblies. An alternative approach to artificial intelligence. Berlin, Heidelberg, New York 1982. Rojas, R.: Theorie der neuronalen Netze – Eine systematische Einführung. Berlin, Heidelberg, New York 1993.
Spracherkennung: Die Erkennung menschlicher gesprochener Sprache ist eines der größten Probleme der neuronalen Netze. In jüngster Zeit gelang jedoch die Herstellung künstlicher neuronaler Netze, die sogar die menschliche Spracherkennung noch übertreffen. Diese Netze bestehen aus lediglich 11 künstlichen Neuronen (mit 30 Verbindungen), die jedoch – anders als die "herkömmlichen" Neurone anderer Netze – nicht nur auf die Intensitäten von Signalen reagieren, sondern auch sensitiv für deren zeitliche Strukturen sind; die einzelnen Neurone arbeiten mit variablen Zeittakten und geben die Signale ähnlich weiter wie Nervenzellen im Hippocampus, in dem das assoziative Lernen beim Menschen stattfindet. In Testläufen nach den Trainingsphasen erweisen sich solche Netze gegenüber dem menschlichen Gehör als überlegen in bezug auf das selektive Herausfiltern einer bestimmten Stimme aus einem Hintergrundrauschen.
Tab. 1: Entwicklungszyklus für technische neuronale Netze
(die wichtigsten Schritte bei der Anwendung künstlicher neuronaler Netze).
0) Wieviele Daten? Lehrersignal? Bewertung?
1) neuronales Modell auswählen
2) Daten als neuronalen Inputvektor darstellen
3) Daten aufteilen für Training und Test
4) Parameter festlegen (Architektur, Aktivierung, Lernregel)
5) Variablen initialisieren
6) Abbruchkriterien festlegen
7) Iteration ausführen (häufig 2 Phasen: Training und Test)
8) Auswerten: Fehlermaße bestimmen
9) Wenn nicht zufrieden, zurück zu 1), 2) oder 4)
Die Schritte 4) bis 8) müssen in der Anwendung häufig mehrfach zyklisch wiederholt werden, bis ein zufriedenstellendes Endergebnis erreicht wird.
neuronale Netze
Tab. 2: Grundtypen technischer neuronaler Netze
Netze mit Lehrer
- Perzeptron
- Hetero-Assoziation
- Backpropagation-Netze
- Netze aus radialen Basisfunktionen
- Reinforcement-Lernen
Netze mit Konkurrenz
- Kohonen-Karte
- K-means Clusteranalyse
- Learning Vector Quantisation
- Adaptive Resonanz-Theorie
Netze mit Rückkopplung
- Hopfield-Netze
- Auto-Assoziation
- Boltzmann-Maschine
neuronale Netze
Lernverfahren:
Bei den Lernverfahren unterscheidet man zwischen unüberwachtem und überwachtem Lernen. Beim überwachten Lernen wird dem System durch ein zusätzliches "Lehrersignal" entweder eine Bewertung des Systemoutputs oder sogar der erwünschte Outputwert Tj für jedes Outputneuron j mitgeteilt. Beim unüberwachten Lernen gibt es kein solches Lehrersignal, und die Aufgabe des Systems besteht gewöhnlich darin, die Struktur der Inputsignale wiederzugeben. Hierzu wird häufig eine lokale oder globale Inhibition zwischen den Ausgangsneuronen eingesetzt (winner-takes-all network), also eine Art Konkurrenz zwischen den Ausgangsneuronen, die dafür sorgt, daß im wesentlichen nur eines von ihnen aktiv ist, nämlich dasjenige, welches am besten zum Input paßt (in Tab. 3 ist der Index des "Gewinnerneurons" mit j* bezeichnet). In Verfahren mit Konkurrenz lernt häufig nur das Gewinnerneuron j*, d.h., nur die Synapsen cij* werden verändert.
neuronale Netze
Tab. 3: gebräuchlichste Netztypen in der technischen Anwendung
| ||||
| Hetero-Assoziation | Lehrer | Schwelle θ | xi · Tj | |
| einfaches Perzeptron | Lehrer | – | l · xi · (Tj – aj) | |
| Backpropagation-Netze, Mehrschicht-Perzeptron | Lehrer, Mehrschicht | l(t), Architektur | l · xi · δj | |
| RBF | Lehrer, Mehrschicht, Distanz | Architektur | l · (xi – cij) · δj | |
| Kohonen-Karte | Konkurrenz, (Distanz) | l(t), N(t) | l · N(j,,j*) · (xi – cij) | |
| adaptives k-means-Netz | Konkurrenz, Distanz | l(t), k | l · (xi – cij)1[j=j*] | |
| LVQ | Konkurrenz, Distanz | l(t), 0 < b < 1 | l · (xi – cij) · (Tj – baj) | |
| ART | Konkurrenz, Vigilanz, Mehrschicht, Rückkopplung | viele | komplizierter | |
| Hopfield-Netze | Rückkopplung, (Stochastik) | – | aj · aj ∈ {-1,1} | |
| Auto-Assoziation | Rückkopplung | θ | aj · aj ∈ {0,1} | |
| Boltzmann-Maschine | Rückkopplung, Stochastik | β(t) | komplizierter |
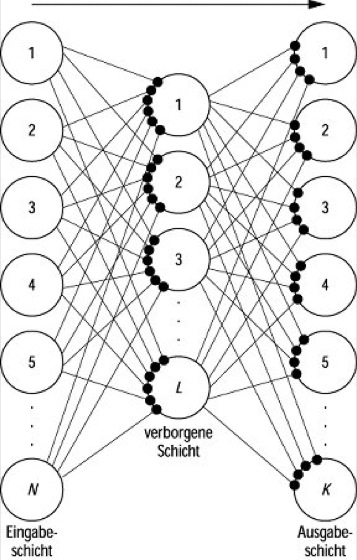
neuronale Netze
Abb. 2: Dreischichtiges Netzwerk mit N Eingabeneuronen, L verborgenen Neuronen und K Ausgabeneuronen. Schwarze Punkte symbolisieren Synapsen; der Pfeil gibt die Richtung des Signalflusses an.

Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.