Lexikon der Physik: Spezielle Relativitätstheorie
Spezielle Relativitätstheorie
Martin Schön, Konstanz
1 Einleitung
Gegen Ende des 19. Jahrhunderts schien die Physik zu einem Abschluß gekommen zu sein. Alle wesentlichen Fragen schienen geklärt zu sein; was noch blieb, war Detailarbeit. Einige doch recht grundlegende Probleme widersetzten sich allerdings hartnäckig einer befriedigenden Lösung. Zu diesen gehörte die Tatsache, daß die Maxwell-Gleichungen nicht Galilei-invariant waren. Offensichtlich galten sie nur in einem einzigen Inertialsystem, welches man Äthersystem nannte (Äther-Hypothese). Alle Versuche, diesen Äther experimentell zu belegen, scheiterten jedoch. Der wohl bekannteste dieser Versuche ist das Michelson-Morley-Experiment. Hierbei wird ein Lichtstrahl geteilt; beide Teilstrahlen durchlaufen anschließend eine Strecke gleicher Länge, bevor sie wieder vereinigt werden. Sollte die Ätherhypothese zutreffen, dann sollten sich nur im Äthersystem die Lichtsignale mit der Vakuumlichtgeschwindigkeit c = 2,997925 · 108 m / s bewegen. Nimmt man an, daß die Erde bei ihrem Lauf um die Sonne sich mindestens einmal mit mindestens 30 km / h relativ zum Äther bewegt, so müßten sich die Lichtstrahlen in unterschiedlichen Richtungen mit unterschiedlichen Geschwindigkeiten ausbreiten. Dann aber dürften die beiden Teilstrahlen im Michelson-Morley-Experiment nicht gleichzeitig auf dem Schirm ankommen, was sich durch Interferenzerscheinungen bemerkbar machen sollte. Dergleichen wurde aber nicht beobachtet.
In den Jahren nach der erstmaligen Durchführung dieses Experiments 1887 gab es einige Lösungsvorschläge (u. a. von Lorentz, der einen Einfluß des Weltäthers auf die Länge der Arme des Michelson-Interferometers annahm), die jedoch wenig überzeugend waren. Interpretiert man das Michelson-Morley-Experiment dahingehend, daß die Maxwell-Gleichungen in allen Inertialsystemen gelten, so bewegt sich Licht unabhängig von der Bewegung der Lichtquelle (dies wird auch durch Doppelsternbeobachtungen gestützt) und unabhängig vom Beobachter (Inertialsystem) stets mit der gleichen Geschwindigkeit c. Bei dieser Argumentation wurde implizit das Relativitätsprinzip verwendet, welches besagt, daß alle Inertialsysteme gleichberechtigt sind. Das Relativitätsprinzip wurde für die Mechanik allgemein anerkannt, nicht jedoch für die Elektrodynamik. Der negative Ausgang des Michelson-Morley-Experiments legt jedoch eine Verallgemeinerung des Relativitätsprinzips auch für elektromagnetische Erscheinungen wie etwa die Lichtausbreitung nahe.
Fassen wir nun unser bisheriges Wissen über die Lichtausbreitung in den beiden folgenden Prinzipien zusammen:
• Prinzip der Konstanz der Lichtgeschwindigkeit: Ein Lichtsignal breitet sich im Vakuum in jedem Inertialsystem mit der gleichen Geschwindigkeit c aus – unabhängig vom Bewegungszustand der Lichtquelle.
• Relativitätsprinzip: Alle Inertialsysteme sind bezüglich allen physikalischen Erscheinungen gleichberechtigt.
Offenbar sind die klassischen Vorstellungen von Raum und Zeit (die ihren Niederschlag in den Galilei-Transformationen finden) nicht mit diesen beiden Prinzipien verträglich. Im Rahmen der klassischen Raum-Zeit-Struktur ist es absurd, wenn man einem sich mit c fortbewegenden Lichtsignal nacheilt und dennoch wieder die gleiche Geschwindigkeit c mißt. Die klassische Raum-Zeit-Struktur muß also revidiert werden. Diese Aufgabe wurde von A. Einstein in seiner 1905 in der Zeitschrift Annalen der Physik erschienenen Arbeit ›Zur Elektrodynamik bewegter Körper‹ gelöst; sie ist Gegenstand des nun folgenden Abschnitts.
2 Relativistische Raum-Zeit-Struktur, Kinematik
Wie wir in der Einleitung sahen, lassen sich die beiden aus der Erfahrung und auf dem Wege der postulierenden Verallgemeinerung gewonnenen Prinzipien Konstanz der Lichtgeschwindigkeit und Relativitätsprinzip nicht mit den klassischen Vorstellungen von Raum und Zeit in Einklang bringen. Eine Revision der klassischen Vorstellungen von Raum und Zeit ist unumgänglich.
Die beiden oben genannten Prinzipien erweisen sich als ausreichend für die Ergründung der neuen, relativistischen Raum-Zeit-Struktur. Es gibt hierfür mehrere mögliche Vorgehensweisen, solche mehr abstrakt-mathematischer Natur und eher physikalisch-anschauliche. Erstere haben den Vorteil, elegant und überschaubar zu sein, während für letztere ein höheres Maß der Anschaulichkeit und konzeptioneller Klarheit spricht. Wir skizzieren hier einen Weg, der operational die notwendigen physikalischen Begriffe konstruiert und letzterer Vorgehensweise zuzuordnen ist.
Stellen wir uns die Aufgabe, mittels Uhren und Maßstäben die neue Raum-Zeit-Struktur zu ergründen. Wir wollen zu diesem Zweck Standarduhren und Standardmaßstäbe verwenden. Als Standardmaßstäbe benutzen wir einfach starre Körper (der Begriff Starrheit in der Relativitätstheorie weist Probleme auf, wenn beschleunigte Bewegungen betrachtet werden; wir fassen aber zunächst nur unbeschleunigte Bewegungen ins Auge), als Standarduhren sog. Lichtuhren. Letztere bestehen einfach aus zwei Spiegeln mit wohldefiniertem Abstand, zwischen denen ein Lichtsignal hin- und herpendelt. Außerdem sei ein Zählwerk angebracht, welches die Zahl der Perioden aufzeichnet. Wir verwenden hier Lichtuhren, weil wir auf Grund der beiden Prinzipien ein hinreichend großes Wissen über das Verhalten von Licht haben und beurteilen können, was passiert, wenn sich die Lichtuhr bewegt.
Bauen wir nun mit diesen beiden Ingredienzen Bezugssysteme auf. Hierzu errichten wir mit den Maßstäben ein starres Gitter und positionieren in jedem Knotenpunkt eine Lichtuhr. Um eine einheitliche Zeit des Bezugssystems zu gewinnen, müssen wir die Uhren noch geeignet synchronisieren. Sobald dies geschehen ist, kann die sog. Einweglichtgeschwindigkeit eines sich von Punkt A nach Punkt B bewegenden Lichtsignals gemessen werden (durch Vergleich der Anzeigen der beiden Uhren bei Start und Ankunft). Zuvor ist nur die sog. Zweiweglichtgeschwindigkeit meßbar (hierzu ist nur eine Uhr nötig; man sendet nämlich bei diesem Experiment ein Signal von A nach B, reflektiert es dort und sendet es wieder nach A zurück). Es stellt sich die Frage, ob man hier eine Wahlfreiheit hat oder ob die Einweglichtgeschwindigkeit empirisch bestimmt werden kann. Diese Frage war der Ausgangspunkt einer langen, bis heute noch nicht abgeschlossenen Diskussion (Reichenbach-Grünbaum-Debatte). Wir wollen diese aber an dieser Stelle nicht weiter vertiefen, sondern schreiten pragmatisch fort und wählen die einfachste und natürlichste Synchronisationsmethode: Wir schicken ein Lichtsignal von A nach B und wieder nach A zurück und stellen die Uhr in B so ein, daß sie bei Reflexion genau das arithmetische Mittel zwischen Abgangszeit und Wiederkehrzeit in A (angezeigt durch die dort befindliche Uhr) anzeigt. So verfahren wir mit allen Uhren unseres Bezugssystems und nennen dann die so gewonnene Zeit die Zeit des Bezugssystems.
Anschließend konstruieren wir auf die gleiche Weise ein zweites Bezugssystem, welches sich gegenüber dem ersten mit der Geschwindigkeit v in x-Richtung bewegen möge, und synchronisieren auch in diesem die Uhren. Nun können wir untersuchen, wie die von den Uhren des zweiten Bezugssystems ![]()
angezeigten Zeiten mit denjenigen des von den Uhren des ersten Bezugssystems ![]()
angezeigten Zeiten zusammenhängen. Konkret geht es um folgendes Problem: In ![]()
werde am Ort x zur Zeit t, gemessen mit den zu ![]()
gehörenden Uhren und Maßstäben, ein Ereignis konstatiert (z. B. ein Aufblitzen einer Lampe). In ![]()
hat dieses Ereignis also die Koordinaten ![]()
. Welche Koordinaten ![]()
hat das Ereignis in ![]()
? Welche ![]()
-Uhr mit welcher Koordinate ![]()
befindet sich beim Aufblitzen gerade am Ort des Aufblitzens, und welche Zeit ![]()
zeigt dann diese Uhr an?
Mit Hilfe der beiden grundlegenden Prinzipien läßt sich dieses Problem lösen. Zunächst einmal gewinnt man aus ihnen drei kinematische Effekte der neuen Raum-Zeit-Struktur: Relativität der Gleichzeitigkeit, Zeitdilatation und Lorentz-Kontraktion. Zwei Ereignisse sind gleichzeitig in einem Bezugssystem ![]()
, wenn die an den jeweiligen Orten befindlichen und in ![]()
gemäß obiger Vorschrift synchronisierten Uhren die gleiche Zeit anzeigen. Dies ist äquivalent dazu, daß zwei simultan von der örtlichen Mitte zwischen diesen beiden Uhren abgehende Lichtsignale bei Ankunft mit den beiden Ereignissen koinzidieren (siehe Abb. 1 ). Betrachtet man nun diesen Vorgang vom relativ zu ![]()
sich mit der Geschwindigkeit ![]()
bewegenden Inertialsystem ![]()
aus, so werden diese beiden Ereignisse dort nicht mehr als gleichzeitig beurteilt. Die Uhr am Ort des ›linken‹ Ereignisses eilt dem Synchronisationssignal entgegen, die andere entfernt sich von diesem (siehe Abb. 1 ). Da die Lichtgeschwindigkeit auch in ![]()
gleich c ist, kommen beide nicht mehr gleichzeitig an. Als Korollar ergibt sich sofort, daß die im Inertialsystem ![]()
synchronisierten Uhren vom Beobachter ![]()
nicht mehr als synchron konstatiert werden (und umgekehrt). Gleichzeitigkeit ist also relativ, und die Verwendung von Begriffen wie ›jetzt‹ oder ›in diesem Augenblick‹ macht nur Sinn, wenn sie auf ein bestimmtes Bezugssystem bezogen werden.
Die Zeitdilatation gewinnt man aus der Analyse einer sich bewegenden Lichtuhr. Vom ruhenden Beobachter aus betrachtet beschreibt das Lichtsignal die in Abb. 2 dargestellte Dreiecksbahn. Da die Lichtgeschwindigkeit aber nach wie vor c ist (obwohl sich die ›Lichtquelle‹ (unterer Spiegel der Lichtuhr) nun bewegt), leuchtet sofort ein, daß der ruhende Beobachter eine längere Dauer der durch das Hin- und Herpendeln des Signals definierten Zeiteinheit konstatiert. Die bewegte Uhr geht also im Vergleich zu den im Inertialsystem ![]()
ruhenden Uhren verlangsamt. Umgekehrt beurteilt der Beobachter ![]()
eine ![]()
-Uhr als verlangsamt gehend. Wegen der Relativität der Gleichzeitigkeit (es wird nicht an denselben Raumpunkten verglichen!) liegt hier kein Widerspruch vor.
Die Länge eines sich bewegenden Stabes kann durch gleichzeitiges Ablesen der beiden Enden bestimmt werden. Wegen der Relativität der Gleichzeitigkeit wird unmittelbar einsichtig, daß die so gemessene Länge vom Bezugssystem abhängig ist. Eine genauere Analyse ergibt, daß ein sich bewegender Stab als verkürzt gemessen wird. Aus dem oben Gesagten ergibt sich, daß hier weder eine reale, ›physikalische‹ Verkürzung (der Stab wird nicht zusammengepreßt) noch eine ›optische Täuschung‹ vorliegt. Es liegt ein objektives Resultat vor, das jedoch nicht absolut ist.
Führt man die hier skizzierten Analysen quantitativ durch, so erhält man folgende Beziehungen:
Relativität der Gleichzeitigkeit:
Zwei in ![]()
gleichzeitige Ereignisse, deren in ![]()
gemessene Koordinatendifferenz ![]()
beträgt, weisen in ![]()
eine zeitliche Koordinatendifferenz ![]()
auf.
Zeitdilatation:

Dabei ist ![]()
die in ![]()
gemessene Zeit (etwa eine Periode zwischen zwei aufeinanderfolgenden Ticks einer Uhr) und ![]()
die in ![]()
gemessene Zeit für diesen Vorgang. Wegen ![]()
dauert der Vorgang aus der Perspektive des Inertialsystems ![]()
folglich länger als aus der Perspektive des Inertialsystems ![]()
(in welchem die ins Auge gefaßte Uhr ruht).
Längenkontraktion:
Dabei ist ![]()
die im mitbewegten Inertialsystem ![]()
gemessene Länge des Stabes (auch Ruhelänge genannt). ![]()
ist die in ![]()
gemessene Länge dieses Stabes. Wegen ![]()
ist die gemessene Länge kleiner als die Ruhelänge; der Stab erscheint verkürzt. Setzt man die oben besprochenen Effekte der speziellrelativistischen Raum-Zeit-Struktur zusammen, so erhält man schließlich die gesuchten Transformationsbeziehungen zwischen den Koordinaten ![]()
eines Ereignisses im Inertialsystem ![]()
und den Koordinaten ![]()
desselben Ereignisses in ![]()
(man nimmt hierbei an, daß die Ursprünge beider Systeme zur Ursprungszeit ![]()
koinzidieren). Diese werden Lorentz-Transformationen genannt und lauten (in drei Dimensionen):

Aus den Lorentz-Transformationen folgt unmittelbar, daß der Ausdruck
invariant gegenüber einem Wechsel des Inertialsystems ist. Dies folgt auch unmittelbar aus dem Prinzip der Konstanz der Lichtgeschwindigkeit, da ![]()
die Ausbreitung einer Lichtwelle vom Ursprung zur Zeit ![]()
beschreibt. Verzichtet man auf die Koinzidenz der Ursprünge beider Systeme für ![]()
, so muß man in (8) zu Koordinatendifferenzen ![]()
, etc. übergehen.
Man beachte die Analogie zur Geometrie der ebenen Fläche. Der Abstand ![]()
zwischen zwei Punkten ist gegeben durch:
falls ein kartesisches Koordinatensystem zugrunde gelegt wird. Auch dieser Ausdruck ist forminvariant beim Übergang von einem kartesischen zu einem anderen kartesischen Koordinatensystem. Durch die Existenz eines gegenüber Koordinatentransformationen invarianten Abstands erhält die Fläche eine geometrische Struktur, die x und y verknüpft. Analog erhält durch die Existenz eines gegenüber Koordinatentransformationen invarianten Ereignisintervalls ![]()
die Raum-Zeit eine geometrische Struktur und wird zur Raumzeit. Die räumlichen und zeitlichen Koordinaten sind nun im Unterschied zur klassischen Galilei-Raum-Zeit miteinander verknüpft! Da die speziellrelativistische Raumzeit eine geometrische Struktur besitzt, kann sie flach oder gekrümmt sein. In der Allgemeinen Relativitätstheorie lernt man, daß die Raumzeit genau dann flach ist, wenn keine Materie vorhanden ist, also ein leeres Universum vorliegt, so wie wir es hier idealisierend angenommen haben. In der galileiischen Raum-Zeit machen derartige Begriffe keinen Sinn. Dort könnte im Prinzip der Raum gekrümmt sein, nicht aber die Raum-Zeit. Raumzeit-Diagramme dienen auch in der Speziellen Relativitätstheorie zur Veranschaulichung von Bewegungen. Sie werden hier Minkowski-Diagramme genannt. Im Unterschied zur klassischen Kinematik repräsentieren sie darüber hinaus eine geometrische Struktur.
Aus den Lorentz-Transformationen lassen sich durch eine einfache Rechnung die Additionstheoreme gewinnen, welche die Transformation von Geschwindigkeiten beschreiben. Bewegt sich ein Körper relativ zum Inertialsystem ![]()
mit der Geschwindigkeit ![]()
, so hat er im Inertialsystem ![]()
die Geschwindigkeit ![]()
:
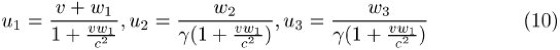
Dabei wurde wieder angenommen, daß sich ![]()
relativ zu ![]()
mit der Geschwindigkeit ![]()
bewegt. Der in der Speziellen Relativitätstheorie oft verwendete Gammafaktor ist eine Abkürzung für ![]()
. Die Geschwindigkeiten addieren sich also nicht einfach wie in der klassischen Galilei-Raum-Zeit. Weitere wichtige kinematische Effekte sind der relativistische Doppler-Effekt sowie die relativistische Aberration.
3 Kovariante Formulierung
Die mathematische Struktur der relativistischen Raumzeit wird durch den Tensorkalkül transparent. Im vorigen Abschnitt wurde gezeigt, daß das Ereignisintervall ![]()
invariant unter Koordinatentransformationen, die von einem Inertialsystem in ein anderes führen, ist. Anstelle von (8) können wir dieses kurz schreiben als
wobei ![]()
der vierdimensionale Ereignisvektor und ![]()
die sogenannte Minkowski-Metrik![]()
ist. Man beachte die Einsteinsche Summenkonvention (über doppelt auftretende Indizes ist zu summieren). Aus der Invarianz von ![]()
gegenüber einer Transformation von einem Inertialsystem in ein anderes folgt sofort:
d. h. die Minkowski-Metrik hat in allen Inertialsystemen die gleiche Gestalt.
Die verdimensionalen Ereignisvektoren ![]()
transformieren sich gemäß den Lorentz-Transformationen (der Einfachheit halber beschränken wir uns auf Transformationen zwischen Inertialsystemen, deren Ursprünge zur Zeit ![]()
koinzidieren; ansonsten müßten anstatt ![]()
die Intervalle ![]()
betrachtet werden):
wobei die Transformationsmatrix ![]()
direkt aus den Lorentz-Transformationen (4)-(7) abgelesen werden kann. Man bezeichnet nun jede vierkomponentige Größe ![]()
, deren Komponenten sich gemäß (13) transformieren, als kontravarianten Vierervektor. Entsprechend bezeichnet man Größen ![]()
mit 2 Indizes, welche sich wie ein Produkt zweier kontravarianter Vektoren transformieren, also:
als kontravariante Tensoren zweiter Stufe. Die Verallgemeinerung auf kontravariante Tensoren n-ter Stufe erfolgt sinngemäß. Invarianten unter Transformationen von einem Inertialsystem in ein anderes wie etwa das Ereignisintervall ![]()
bezeichnet man als Skalare oder Tensoren nullter Stufe. Der Tensorbegriff läßt sich auch für beliebige Koordinatentransformationen einführen. Man muß dann anstelle von ![]()
den infinitesimalen Ereignisvektor ![]()
betrachten. Größen, die sich wie der infinitesimale Ereignisvektor oder wie Produkte desselben transformieren, sind dann kontravariante Tensoren. In der Allgemeinen Relativitätstheorie werden solche beliebigen Koordinatentransformationen ausgiebig verwendet; hier aber genügt es, sich mit Inertialsystemen zu befassen. Man führt auch kovariante Tensoren ein: Diese transformieren sich wie der Gradient eines Skalars oder Produkte desselben. Für einen kovarianten Vektor ![]()
etwa gilt:
wobei ![]()
die Inverse der Lorentz-Transformationsmatrix ist.
Man kann zeigen, daß die Metrik ein kovarianter Tensor zweiter Stufe ist, der zudem für Transformationen von einem Inertialsystem in ein anderes die Besonderheit besitzt, dabei seine Komponenten nicht zu ändern, also
mit ![]()
. Beziehung (16) eröffnet eine weitere Möglichkeit, die Transformationsmatrix ![]()
und damit die Lorentz-Transformationen abzuleiten.
Man kann zeigen, daß Summen von Tensoren gleicher Stufe wieder Tensoren derselben Stufe sind. Tensoren verschiedener Stufen lassen sich multiplizieren, und man erhält einen Tensor, dessen Stufe gleich der Summe der Stufen der Faktoren ist (Tensoralgebra). Man kann auch Ableitungen von Tensoren definieren (kovariante Ableitung, Tensoranalysis). Bei der in der Speziellen Relativitätstheorie üblichen Beschränkung auf Inertialsysteme reduziert sich die kovariante Ableitung auf die gewöhnliche Ableitung.
Der Vorteil der Verwendung des Tensorkalküls in der Relativitätstheorie ist folgender. Tensoriell formulierte Gleichungen sind automatisch in allen Koordinatensystemen gültig, wenn sie in einem einzigen gültig sind. Dies folgt sofort aus dem Transformationsverhalten von Tensoren. Man nennt derart formulierte Gleichungen auch kovariant formulierte.
Wir haben hier den Tensorbegriff pragmatisch eingeführt. Mathematisch ist ein Tensor nichts anderes als eine multilineare Abbildung vom Raum der Vektoren in die reellen Zahlen. Dies soll an dieser Stelle jedoch nicht vertieft werden (Tensor).
4 Relativistische Dynamik
Zwei Aufgaben stellen sich: Zum einen ist die kovariante Formulierung des Newtonschen Kraftgesetzes zu finden, zum anderen Erhaltungssätze. Beginnen wir mit letzterem.
Aus der Newtonschen Mechanik, die für kleine Geschwindigkeiten weiterhin gültig sein muß, wissen wir, daß der Impuls ![]()
in einem abgeschlossenen System erhalten ist. Ein einfaches Gedankenexperiment zeigt sofort, daß dies für beliebige Geschwindigkeiten nicht mehr gelten kann: Man lasse eine Kugel der Masse ![]()
mit der Geschwindigkeit ![]()
senkrecht gegen eine im Inertialsystem ![]()
ruhende Wand prallen (siehe Abb. 3 ). Die Kugel möge eine Strecke ![]()
in die Wand eindringen und dann zur Ruhe kommen. Die Eindringtiefe ![]()
ist ein Maß für den Impuls der Kugel. Anschließend betrachte man diesen Vorgang im System ![]()
, welches sich mit der Geschwindigkeit ![]()
parallel zur Wand bewege. Auf Grund der Additionstheoreme ist dann die Geschwindigkeitskomponente senkrecht zur Wand relativ zu ![]()
gegeben durch: ![]()
. Da senkrecht zur Bewegungsrichtung keine Lorentz-Kontraktion stattfindet, beträgt auch die in ![]()
gemessene Eindringtiefe ![]()
. Folglich konstatiert ![]()
die gleiche Impulskomponente senkrecht zur Wand wie ![]()
. Da jedoch die entsprechende Geschwindigkeitskomponente ![]()
ungleich ![]()
ist, kann die Masse nicht in beiden Systemen die gleiche sein (sonst würde sich das Produkt aus Masse und Geschwindigkeit ändern).
Der relativistische Impuls kann also nicht ![]()
lauten. Wir machen nun folgenden Ansatz für den relativistischen Impuls: ![]()
, lassen also eine Geschwindigkeitsabhängigkeit der Masse zu. Das ist die einfachste Verallgemeinerung des Newtonschen Impulses. Man kann nun zeigen, daß die Gültigkeit der Impulserhaltung (mit obigem Ansatz) in allen Inertialsystemen (das fordert das Relativitätsprinzip) impliziert, daß ![]()
folgende Gestalt hat:

Dabei ist ![]()
die Ruhemasse. Damit ist noch nicht die Impulserhaltung bewiesen, diese muß experimentell überprüft werden. Dies ist aber in hervorragender Übereinstimmung mit der Theorie gelungen.
Die Raumzeit-Struktur der Speziellen Relativitätstheorie erfordert die Abhängigkeit der Masse von der Geschwindigkeit nach Maßgabe von (17) (falls, wie experimentell bestätigt worden ist, der daraus konstruierte relativistische Impuls ![]()
in allen Inertialsystemen erhalten ist). Man beachte, daß dieser relativistische Dreierimpuls![]()
(›Dreier-‹, weil er drei Komponenten besitzt) kein Vierervektor ist. Man kann aber aus ihm einen solchen konstruieren. Versuchen wir, einen Vierervektor zu bauen, dessen Komponenten ![]()
enthalten. Dann können wir nämlich ein Lemma der Tensorrechnung anwenden, welches besagt, daß aus der Erhaltung einer Komponente eines Vierervektors in allen Inertialsystemen die Erhaltung sämtlicher Komponenten dieses Vektors folgt. Aus der Erhaltung von ![]()
in allen Inertialsystemen folgt dann die Erhaltung dieses ganzen Vektors. Das aber bedeutet, daß auch die vierte Komponente dieses Vierervektors erhalten sein muß. Wir erhalten also automatisch einen weiteren Erhaltungssatz.
Offensichtlich ist ![]()
ein Vierervektor ( ![]()
ist die sog. Eigenzeit; man stelle sich vor, daß die Bahnkurve des Teilchens in der Raumzeit durch ![]()
parametrisiert ist: ![]()
). Multiplikation mit der Ruhemasse ![]()
, die ein Skalar ist, ergibt wieder einen Vierervektor. Dessen räumliche Komponenten sind genau diejenigen von ![]()
! Definieren wir also als Viererimpulsvektor:
Nach oben Gesagtem folgt aus der Erhaltung des relativistischen Dreierimpulses die Erhaltung von ![]()
und damit von ![]()
. Die relativistische Masse ist also erhalten. Wie können wir diese interpretieren?
Entwickeln wir den Ausdruck (17) für die relativistische Masse bis zur zweiten Ordnung, so erhalten wir:

Der zweite Summand ist die kinetische Energie dividiert durch das Quadrat der Lichtgeschwindigkeit. In zweiter Ordnung ist die relativistische Masse also gleich der Ruhemasse plus kinetische Energie dividiert durch ![]()
. Zusätzliche Energie scheint also einen zusätzlichen Massenbeitrag zu liefern, und zwar gemäß ![]()
. Postulieren wir also mit Einstein:
Die relativistische Energie ist erhalten, falls die relativistische Masse erhalten ist. Das ist – wie wir oben sahen – der Fall, falls der relativistische Dreierimpuls erhalten ist. Ferner sehen wir, daß relativistischer Dreierimpuls und relativistische Energie dividiert durch c einen Vierervektor bilden. Wir können nämlich schreiben: ![]()
. Dieser Vierervektor heißt auch Energie-Impuls-Vektor. Damit ist auch das Transformationsverhalten von Impuls und Energie beschrieben.
Herzstück der Newtonschen Mechanik ist das Konzept der Kraft. Kennen wir diese sowie den Anfangszustand, so sind wir zumindest theoretisch in der Lage, den Zustand eines Systems zu jedem beliebigen Zeitpunkt zu berechnen. Gibt es etwas Analoges in der relativistischen Mechanik?
Definieren wir folgenden Vierervektor:
dabei sei ![]()
die Weltlinie des Teilchens, parametrisiert durch die Eigenzeit. Falls wir ![]()
kennen, können wir mit Hilfe von (21) die Bewegung des Teilchens bestimmen. Wir nennen ![]()
die relativistische Viererkraft und fragen uns, wie sie bei gegebener physikalischer Situation bestimmt werden kann. Das ist analog zur klassischen Physik, wo ja auch erst unabhängig vom zweiten Newtonschen Axiom gegebene Kraftgesetze aus diesem ein echtes Gesetz machen.
Die relativistische Viererkraft kann nun aus der Kenntnis der Newtonschen Kraft bestimmt werden. Hierzu geht man einfach ins mitbewegte Inertialsystem. Dort gilt wegen ![]()
, wobei ![]()
die Newtonsche Kraft ist, die in diesem Inertialsystem auf das Teilchen wirken sollte. Die Rücktransformation ins ursprüngliche Inertialsystem ergibt dann
Definieren wir die relativistische Dreierkraft![]()
als ![]()
, so läßt sich das auch schreiben als:
Die relativistische Dreierkraft, die natürlich kein Vierervektor ist (wohl aber ein Dreiervektor bezüglich Ortstransformationen) ist also bis auf einen Gammafaktor gleich dem räumlichen Teil der Viererkraft. Wir sind nun in der Lage, diese zu interpretieren. Aus (23) und dem Zusammenhang zwischen Viererkraft und Newtonscher Kraft folgt nämlich ![]()
. Das kann aber wie folgt geschrieben werden: ![]()
. Folglich ist die relativistische Dreierkraft für die geleistete Arbeit maßgeblich; der Energieinhalt eines Körpers, an welchem die Arbeit ![]()
verrichtet wurde, erhöht sich um dieses ![]()
. Mithin ist die relativistische Dreierkraft die richtige relativistische Verallgemeinerung der Newtonschen Kraft ![]()
. Sie ist kein Vierervektor, wohl aber der räumliche Teil eines solchen, falls man sie noch mit einem Gammafaktor multipliziert. Im mitbewegten Inertialsystem sind übrigens der räumliche Teil der Viererkraft ![]()
, die relativistische Dreierkraft ![]()
und die Newtonsche Dreierkraft ![]()
exakt gleich.
5 Elektrodynamik
Die Maxwell-Gleichungen gelten in allen Inertialsystemen, sind also bereits Lorentz-invariant. Allerdings sind sie in der üblichen Form noch nicht manifest kovariant. Wir wissen noch nicht, wie sich die elektrischen und magnetischen Felder transformieren. Um dieses Transformationsverhalten aufzufinden, und um die Maxwell-Gleichungen kovariant zu formulieren, versuchen wir, sie in die Form einer Tensorgleichung zu bringen. Hierzu fassen wir die Ladungsdichte![]()
und die elektrische Stromdichte![]()
zu einem Vierervektor
zusammen (daß dies wirklich ein Vierervektor ist, folgt – unter Annahme der Invarianz der elektrischen Ladung – aus dem Transformationsverhalten der Komponenten). Anschließend definiert man eine Matrix ![]()
wie folgt:

wobei die ![]()
und die ![]()
die Komponenten der magnetischen bzw. elektrischen Feldstärke sind.
Mit diesen Definitionen können die Maxwell-Gleichungen wie folgt formuliert werden:

Da auf den rechten Seiten dieser Gleichungen jeweils kontravariante Vierervektoren stehen, muß ![]()
ein kontravarianter Tensor zweiter Stufe sein. Damit liegt sein Transformationsverhalten und das der elektrischen und magnetischen Felder fest. Man sieht, daß eine allgemeine Lorentz-Transformation die elektrischen und magnetischen Felder ›mischt‹, d.h. ein rein elektrisches Feld (z.B. im mitbewegten Inertialsystem einer Ladung) kann in einem anderen Inertialsystem magnetische Felder hervorrufen (in demjenigen System, relativ zu dem sich diese Ladung bewegt; das ist ein bereits bekanntes Phänomen). Magnetische und elektrische Felder erscheinen nicht länger als zwei verschiedene Felder, sondern repräsentieren ein einziges elektromagnetisches Feld. Dies kommt durch die kovariante Formulierung deutlich zum Ausdruck; die klassische Formulierung verschleierte diesen Zusammenhang.
6 Bedeutung der Speziellen Relativitätstheorie und ihre Grenzen
Die Spezielle Relativitätstheorie setzt gleichsam den Rahmen, in welchen sich andere Theorien einzufügen haben (falls wir die Gravitation vernachlässigen). Eine physikalische Theorie muß nämlich Lorentz-kovariant formuliert werden und den Prinzipien der Speziellen Relativitätstheorie Rechnung tragen. So dürfen etwa keine Überlichtgeschwindigkeiten auftreten. Man kann also zu Recht der Speziellen Relativitätstheorie den Rang einer tragenden Säule der modernen Physik zusprechen.
Die kovariante Formulierung physikalischer Theorien hat viele wichtige Erkenntnisse zutage gefördert. Neben dem oben bereits erwähnten Zusammenhang zwischen Masse und Energie und der Wesensverwandtschaft von elektrischem und magnetischem Feld sind dies beispielsweise die Beziehung zwischen Teilchen und Antiteilchen (Dirac-Theorie) oder unser Verständnis von Spin und magnetischem Moment. Zweifellos hat der Kovarianzgedanke die modernen Eichtheorien wesentlich stimuliert.
Die Spezielle Relativitätstheorie ist eine Theorie der flachen Raumzeit. Während sich die anderen Wechselwirkungen im Rahmen dieser Theorie beschreiben ließen (mittels des hier geschilderten Kraftkonzeptes), gelang dies bei der Gravitation nicht. Nach mehreren Jahren erfolglosen Versuchens fand Einstein schließlich einen anderen Weg: Die Vorstellung einer flachen Raumzeit wurde fallengelassen. Materie krümmt die Raumzeit, es gibt keine endlich ausgedehnten Inertialsysteme mehr, sondern nur noch lokale (die sich ›frei fallend‹ bewegen). In diesen gilt dann die Spezielle Relativitätstheorie, und in diesen ist die Gravitation ›wegtransformiert‹. Dies ist der Inhalt des Äquivalenzprinzips und führt zur Allgemeinen Relativitätstheorie.
Allerdings ist die Forschung hier noch nicht zu einem Abschluß gekommen. Die Vereinigung der Allgemeinen Relativitätstheorie mit der Quantentheorie steht noch aus (Quantengravitation). Quantenfeldtheorien auf gekrümmtem Hintergrund sind bereits erfolgreich konstruiert worden, aber auf dem Gebiet der Quantisierung der Gravitation selbst ist man bisher nicht über Ansätze hinausgekommen. Es ist durchaus vorstellbar, daß die Quantengravitation auch unsere Vorstellung über die flache Raumzeit und damit die Spezielle Relativitätstheorie modifiziert (Modifikationen sind insbesondere ab der Planck-Skala zu erwarten).
Literatur:
W. Rindler: Essential Relativity, Springer-Verlag, 1977.
A.P. French: Special Relativity, New York, 1968.
N.D. Mermin: Space and Time in Special Relativity, New York, 1968.
Spezielle Relativitätstheorie 1: Gleichzeitigkeit in ![]()
aus der Perspektive von S. Der Kasten mit den beiden ![]()
-Uhren bewegt sich gegenüber ![]()
mit v nach rechts. In der Mitte gehen zwei Synchronisationssignale ab.

Spezielle Relativitätstheorie 2: Eine ![]()
-Lichtuhr aus der Perspektive von S; Lichtweg des in der ![]()
-Lichtuhr hin- und herpendelnden Photons, von ![]()
aus gesehen.
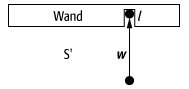
Spezielle Relativitätstheorie 3: Gedankenexperiment zur Impulserhaltung und relativistischen Masse. Die Kugel trifft mit der Geschwindigkeit ![]()
frontal auf eine Wand und dringt eine Strecke ![]()
in diese ein.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.