Wegen großer Probleme im Lateinunterricht verläuft die Schulzeit von Friedrich Wilhelm Bessel nicht gerade glücklich; mit 14 Jahren muss der Sohn eines Justizbeamten den Besuch des Gymnasiums in Minden abbrechen, um einen praktischen Beruf zu erlernen. Er beginnt eine Lehre bei der Import-/Exportfirma Kulenkamp & Söhne in Bremen. An seiner Ausbildungsstätte weiß man bald die rasche Auffassungsgabe und große Zuverlässigkeit des Lehrlings zu schätzen.

Von seinem zweiten Lehrjahr an erhält Bessel – entgegen der sonst üblichen Praxis – einen geringen Lohn, von dem sich der Wissbegierige vor allem Bücher kauft. Abends lernt er Englisch und Spanisch und verbessert seine Kenntnisse in Geographie, um die Transportwege der Güter kennen zu lernen, um deren Transport er sich kümmern muss. Dabei erfährt er von den Schwierigkeiten, die Position eines Schiffs auf hoher See zu bestimmen; dies führt ihn zur Astronomie und damit zur Mathematik.

Er beginnt mit eigenen Himmelsbeobachtungen und -messungen auf einfachen, teilweise selbst entworfenen Instrumenten. Dann studiert er die Beobachtungsnotizen des englischen Mathematikers und Astronomen Thomas Harriot (1560–1621) aus dem Jahr 1607 über die Bahn des Kometen, der später den Namen Halleys erhält. Seine Auswertungen legt er Heinrich Olbers (1758–1840) vor, einem Bremer Arzt und Experten für Kometen, der durch die Entdeckung der Kleinplaneten Pallas und Vesta Berühmheit erlangt hat. Dieser ermuntert ihn zur Fortsetzung seiner Untersuchungen. Als das 330 Seiten umfassende Werk veröffentlicht wird, hat es bereits höchstes wissenschaftliches Niveau. Bessel arbeitet zunächst weiter als Angestellter der Handelsfirma, beschäftigt sich aber von nun an verstärkt im Selbststudium mit Astronomie, Himmelsmechanik und Mathematik. 1806 endlich bietet man ihm eine Assistentenstelle an einem privaten, hervorragend ausgestatteten Observatorium in Lilienthal bei Bremen an, die er trotz der schlechteren Bezahlung annimmt. Jetzt hat er endlich genügend Zeit für intensive Himmelsbeobachtungen; innerhalb von vier Jahren veröffentlicht er 51 wissenschaftliche Arbeiten.

Im Jahr 1807 begegnet er Carl Friedrich Gauß, der von Bessels Arbeiten so beeindruckt ist, dass auf seine Anregung hin die Göttinger Universität dem Schulabbrecher ohne Studium einen Doktortitel verleiht, was Voraussetzung für die Übernahme einer Professur ist. Bessel und Gauß verbindet eine lebenslange Freundschaft mit umfangreichem wissenschaftlichen Briefwechsel.

1810 wird der 26-Jährige als Professor für Astronomie an die Universität von Königsberg in Ostpreußen berufen und mit der Leitung des im Bau befindlichen Observatoriums beauftragt. Trotz der schwierigen wirtschaftlichen Verhältnisse (napoleonische Kriege) wird der Bau des Observatoriums im Jahr 1813 abgeschlossen. In den folgenden Jahren schlägt Bessel alle Stellenangebote aus und bleibt – von wenigen Reisen abgesehen – für den Rest seines Lebens in Königsberg.

Bessel setzt sich das Ziel, ein zuverlässiges »Himmels-Koordinatensystem« aufzustellen, durch das die Position der Himmelskörper exakt angegeben werden kann. Er bestimmt genaue Werte für die Schiefe der Ekliptik (Neigung der Ebene der Erdbahn gegenüber der Äquatorebene), für die jährliche Präzession der Äquinoktien (Vorrücken des Frühlingspunkts, die bedingt ist durch die Richtungsänderung der Rotationsachse der Erde infolge der Anziehungskräfte von Mond und Sonne sowie der Abweichung der Gestalt der Erde von der Kugelform) und für die Nutation der Erde (periodische Schwankung der Erdachse). Er analysiert die Bedingungen, unter denen astronomische Messwerte zustandekommen, entwickelt Theorien darüber, wie die Optik der Instrumente die Messungen beeinflusst, aber auch, welche Rolle Temperatur- und Luftdruckunterschiede spielen.

Außerdem: Das Licht (v = 300 000 km/s) benötigt für das Durchlaufen eines Teleskops eine gewisse Zeit, in der sich die Erde weiterdreht; zum Beispiel bewegt sich die Erde (v = 30 m/s) um 0,5 mm weiter, wenn das Licht seinen Weg durch ein 5 m langes Teleskop nimmt (so genannte Aberration).

Bereits 1807 hat Bessel damit begonnen, die Positionsdaten von 3222 Sternen im Sternenkatalog des englischen Astronomen James Bradley (1693–1762) zu überprüfen; 1818 gibt er ein Buch mit den bereinigten Daten in lateinischer (!) Sprache heraus (»Fundamenta Astronomiae«). 1830 folgen die »Königsberger Tabellen« (Tabulae Regiomontanae), ein 606-seitiges Buch, das neben umfangreichen Erläuterungen zu Präzession, Nutation und Aberration und so weiter Positionstafeln von 38 Sternen enthält, die auch am Tage beobachtet werden können, und zwar für einen Zeitraum von 100 Jahren (1750–1850). Für die Sterne Sirius und Prokyon stellt er die Behauptung auf, dass sie einen – bis dahin nicht beobachteten – Begleiter haben (»dunkle Sterne«), was auch zehn Jahre später bestätigt wird.

Bessel wertet die Ergebnisse der verschiedenen Vermessungen der Gestalt der Erde aus, führt selbst eine Messung längs eines Meridians in Ostpreußen durch und gibt 1841 den Wert 1/299 für die Abweichung des Erd-Ellipsoids von der Kugelgestalt (das später als Bessel-Ellipsoid bezeichnet wird) an, die bis in die Zeit der Erdvermessung durch Satelliten als ausreichend genaue Zahl verwendet wird.

Bessel ist der erste Astronom, dem es gelingt, die Entfernung eines »nahen« Sterns zu bestimmen: Im Prinzip genügen zwei Messungen im Abstand von einem halben Jahr, um die scheinbare Positionsänderung dieses Himmelskörpers als Winkelunterschied (Parallaxe) zu bestimmen.

Im Jahr 1838 misst er in 99 Beobachtungsnächten jeweils die Position des Fixsterns 61 Cygni (61. Stern im Sternbild Schwan) mithilfe eines von Joseph von Fraunhofer (1787–1826), dem Entdecker der Absorptionslinien im Spektrum des Sonnenlichts, entwickelten Heliometers. Nach der Methode der kleinsten Quadrate bestimmt er hieraus einen Parallaxenwinkel von \(0,314''\) (das ist weniger als der zehntausendste Teil eines Winkelgrads) und damit eine Entfernung von ungefähr 10 Lichtjahren (heute wird ein Parallaxenwinkel von \(0,292''\) für gültig angesehen) – dies ist der erste faktische Beweis für die Richtigkeit des Kopernikanischen Weltbilds, also zweifelsohne ein Höhepunkt in der Geschichte der Astronomie.

Auch in der Mathematik hinterlässt der Autodidakt Bessel Spuren: 1812 veröffentlicht er Untersuchungen zum Integral-Logarithmus \(\text{li}(x)=\int_0^x \frac{1}{\ln(t)} dt\), dessen Funktionswerte er mithilfe einer Potenzreihe mit siebenstelliger Genauigkeit bestimmen kann.

1817 entdeckt er bei der Untersuchung der Bewegung von drei Körpern unter Berücksichtigung der gegenseitigen Beeinflussung durch Gravitationskräfte (Drei-Körper-Problem) eine Klasse von besonderen Funktionen, die man heute zu seinen Ehren als Bessel-Funktionen bezeichnet. Es handelt sich dabei um Funktionen, die Differentialgleichungen der Form \(x^2y''+xy'+(x^2 – n^2)\cdot y=0\) mit \(n \in \mathbb{N}_0\) erfüllen.

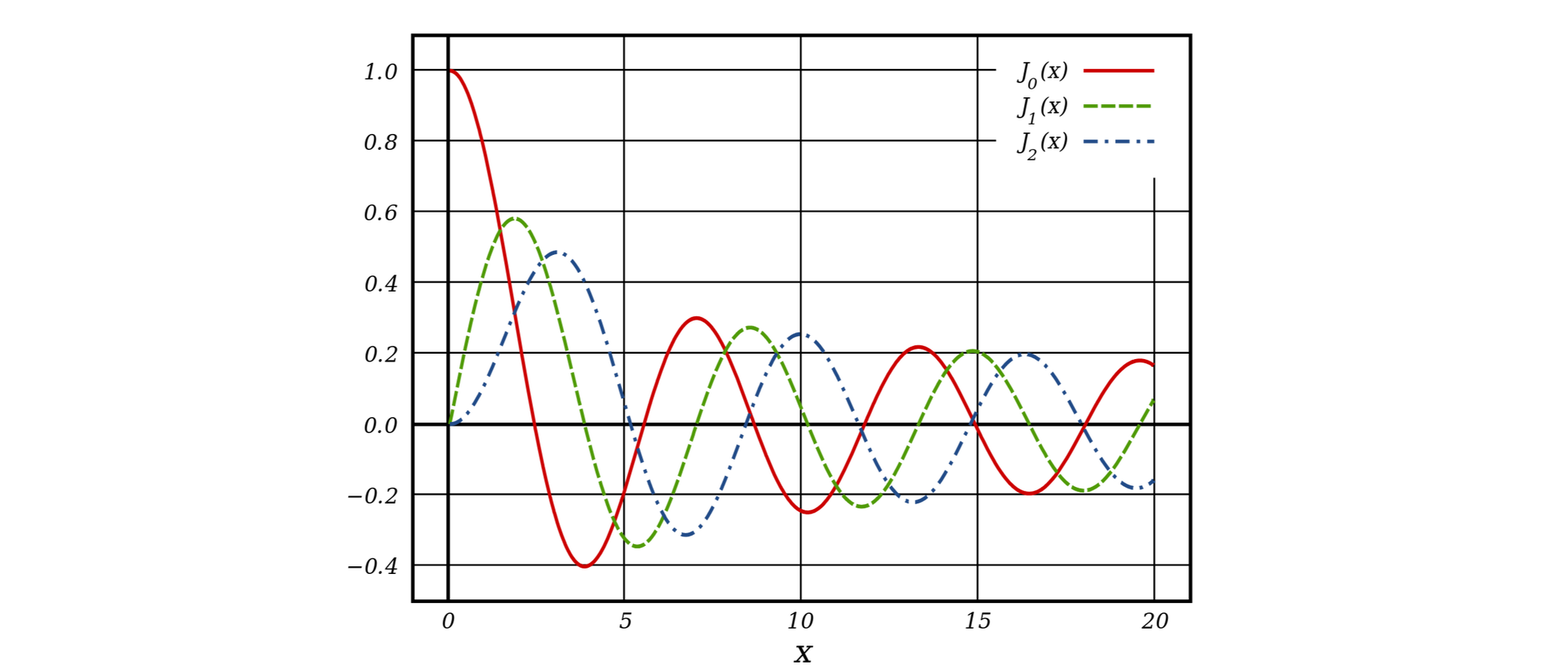
Auf der deutschen Briefmarke von 1984 sind für \(n = 0\) und \(n = 1\) die Graphen der Bessel-Funktionen \(J_n(x)= \frac{1}{\pi} \int_0^\pi \cos \big(nt – x \sin (t)\big)dt\) abgebildet, die sich auch mithilfe von Potenzreihen darstellen lassen: \[J_n(x)= \sum_{k=0}^{\infty} \frac{–1}{k!\cdot (k+n)!} \cdot \left(\frac{x}{2}\right)^{2k+n}\]

Diese Funktionen spielen in vielen Gebieten der Physik eine Rolle, unter anderem bei der Ausbreitung von Wasserwellen, bei der Wärmeleitung in Stäben und bei der Lichtbeugung an kreisförmigen Löchern.

Auch entwickelt er eine Interpolationsformel, bei der zunächst die Differenzen der Funktionswerte an Stützstellen betrachtet werden, dann die Differenzen dieser Differenzen und so weiter (sogenannte Bessel-Interpolation), außerdem beschäftigt er sich intensiv mit der Verteilung von Fehler-Wahrscheinlichkeiten.

Wegen seiner zahlreichen Veröffentlichungen und bahnbrechenden Arbeiten steigt Bessels internationales Ansehen von Jahr zu Jahr. Er erhält den Lalande-Preis der französischen Akademie und wird zum Mitglied der Preußischen Akademie der Wissenschaften gewählt, später auch zum Mitglied der Royal Society sowie zahlreicher anderer wissenschaftlicher Gesellschaften. Von 1840 an verschlechtert sich seine gesundheitliche Verfassung zusehends; 1846 stirbt er nach einer Krebserkrankung.