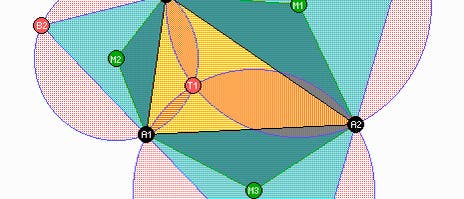
Die Schätze der Wissenschaft sind unerschöpflich. Selbst wer auf einem so abgenutzten Feld wie der klassischen Dreiecksgeometrie gräbt, wird über die Maßen fündig. Erinnern Sie sich aus der Schule noch an die "besonderen Punkte" im Dreieck? Umkreismittelpunkt = Schnittpunkt der Mittelsenkrechten, Inkreismittelpunkt = Schnittpunkt der Winkelhalbierenden, Höhenschnittpunkt und Schwerpunkt = Schnittpunkt der Seitenhalbierenden. Das reicht doch eigentlich, sollte man meinen.

Aber weit gefehlt! Fleißige Dreiecks-Zoologen wissen über 3500 dieser speziellen Punkte samt ihren komplizierten Verwandtschaftbeziehungen aufzuzählen. Und auch Umkreis und Inkreis sind nur die eher langweiligen Vertreter einer ganzen Schar von Kegelschnitten, die treffsicher irgendwelche besonderen Punkte ansteuern oder sich innig an die Dreiecksseiten anschmiegen.

Da können drei Seiten im gedruckten "Spektrum"-Heft (März 2010) nur eine erste zarte Ahnung dieser Pracht liefern. Unser Kolumnist Norbert Treitz (eigentlich Physiker (der diesmal von der physikalischen Bestimmung des Fermat-Torricelli-Punktes (auch einer der besonderen Punkte) unversehens zur Geometrie abgedriftet ist)) hat immer wieder besonders darunter zu leiden, dass die Fülle seiner Schätze (nebst Randbemerkungen, die immer nur kurz vom Thema wegführen) nicht ausreichend Platz findet.

Aber das Internet im Allgemeinen und die Spektrum-Website im Besonderen ist groß und das bewegte Bild für dieses Thema eine wundervolle Darreichungsform. Endlich kann man diese merkwürdigen Kegelschnitte Punkt für Punkt in ihrer Entstehung verfolgen. Genießen Sie Kegelschnitte und die isogonale Abbildung. Ergänzungen zu Torricellis 5. Mittelpunkt des Dreiecks, mit Kurzfilmen!