Schon mehrfach war in dieser Serie von den etwas weniger edlen Brüdern der fünf platonischen Körper die Rede. Sie sind nicht ganz so regelmäßig, dafür aber vielfältiger; die archimedischen Körper. Aber was genau ist ein archimedischer Körper?

Seine Flächen müssen aus regelmäßigen (gleichseitigen und gleichwinkligen) Vielecken bestehen; aber die Vielecke müssen untereinander nicht gleich sein. Mischungen von Dreiecken und Fünfecken (oder auch Sechsecken, Vierecken und Zehnecken) sind zugelassen. Nur die Kantenlänge muss natürlich einheitlich sein, sonst würden die verschiedenen Flächen nicht zusammenpassen.

Wollte man es bei dieser Einschränkung belassen, gäbe es eine unübersichtliche Vielzahl archimedischer Körper, von denen etliche auch noch unerfreulich schief aussehen. Nein – etwas mehr Symmetrie soll es schon sein. Deswegen gehört zur Definition des archimedischen Körpers auch noch, dass "alle Ecken gleich sein" müssen.

Das heißt: Von jeder Ecke aus bietet sich "im Wesentlichen" derselbe Anblick. Wenn ich auf einer Ecke stehe und meinen Blick in die Runde schweifen lasse, sehe ich der Reihe nach (zum Beispiel) ein Fünfeck, ein Viereck, ein Dreieck und noch ein Viereck. Diese Folge von Vielecken soll von jeder Ecke aus gesehen dieselbe sein; allenfalls ist die umgekehrte Reihenfolge erlaubt. Und selbstverständlich kommt es nicht darauf an, bei welcher Fläche man seine Panaromablickübung beginnt; die Folge Viereck, Dreieck, Viereck, Fünfeck ist dieselbe wie die oben angegebene.

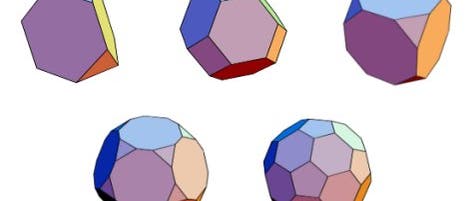
Welche Körper fallen unter die so verschärften Bedingungen? Nun, wir haben beim Entecken und Entkanten (Folge 8 dieser Serie) schon einige von ihnen kennen gelernt. Entecken heißt ja Ecken abschneiden, und zwar alle Ecken in gleichem Maße; wenn man einen Würfel enteckt, kommen als Schnittflächen acht gleichseitige Dreiecke zum Vorschein. Von den quadratischen Seitenflächen des Würfels bleiben Achtecke übrig. Deren Seiten sind abwechselnd Teile der ursprünglichen Würfelkante (die "geraden" Seiten) und solche, die durch den Schnitt neu entstehen (die "schrägen" Seiten). Also gilt es gerade so viel von jeder Ecke abzuschneiden, dass die schrägen Seiten genauso lang werden wie die geraden und damit die Achtecke gleichseitig sind – und schon haben wir unseren ersten archimedischen Körper, den Würfelstumpf.

Das Rezept funktioniert für die Kollegen des Würfels genauso. Wenn man einen platonischen Körper enteckt, der aus n-Ecken besteht, von denen jeweils k Stück in einer Ecke zusammentreffen, dann sind die Schnittflächen regelmäßige k-Ecke, und von den ursprünglichen Flächen bleiben (2n)-Ecke übrig. So kommt man zu den Stümpfen (siehe die Bilder oben). Der Ikosaederstumpf ist uns unter dem Namen Fußball geläufig.

Damit ist die symmetrieerzeugende Kraft des Käsemessers noch lange nicht erschöpft! Man schneide – zum Beispiel – vom Würfel die Ecken immer noch weiter ab, bis den Achtecken die geraden Seiten bis auf null zusammenschrumpfen. Dann bilden die schrägen Seiten so ein Vorfahrtsschild, und das ist auch ein Quadrat, bloß halt ein schräges. Der entstehende Körper heißt Kuboktaeder, weil er eine sehr interessante Mischung aus Kubus (Würfel) und Oktaeder ist. Enteckt man nämlich das Oktaeder so heftig wie den Würfel, kommt ebenfalls das Kuboktaeder heraus.

Dasselbe Spiel angewandt auf das Dodekaeder ergibt einen gemischten Körper mit einem ebenso gemischten Namen: Ikosi-Dodekaeder.

Ebenfalls in Folge 8 dieser Serie hatte ich Ihnen noch eine grundsätzlich andere Art, das Messer zu führen, vorgestellt: das "Entkanten". Man schneide entlang der Kanten, und zwar so, dass von den beiden Flächen, die sich an dieser Kante treffen, genau gleich breite Streifen abgeschnitten werden. Die Schnittfläche hat dann zwei Seiten, die parallel zur soeben weggeschnittenen Kante liegen, aber sie ist nicht einfach ein Rechteck. Denn in den Ecken treffen sich drei oder mehr Schnittflächen von den dort zusammenlaufenden Kanten; dort kommt zu dem Rechteck noch ein kleines Dreieck hinzu, und das an beiden Enden der Kante. Also sind die Schnittflächen langgestreckte Sechsecke. Wenn man die Schnitttiefe richtig wählt, kriegt man diese Sechsecke wohl gleichseitig, aber niemals gleichwinklig. Der Winkel in der Ecke ist einfach unvermeidlich zu spitz. Also ist Entkanten allein zum Erzeugen von Ebenmäßigkeit nicht besonders geeignet.

Aber wenn man die kleinen spitzen Dreieckszipfel auch noch wegschneidet? Das geht, und zwar durch ganz gewöhnliches Entecken. Von den Entkantungs-Schnittflächen bleiben dann tatsächlich nur Rechtecke übrig, und der Rest ist einfach. Man stelle die beiden Schnitttiefen fürs Entkanten und Entecken so ein, dass das Entkantungsrechteck ein Quadrat ist, und schon haben wir einen archimedischen Körper. Das Entecken selbst produziert nämlich in diesem Fall wieder gleichseitige k-Ecke, wobei k die Anzahl der in dieser Ecke zusammentreffenden Kanten ist.

Aus dem Würfel macht dieses Verfahren einen Körper, der als "Rhomben-Kuboktaeder" in den Lehrbüchern steht. Der Name stammt von Johannes Kepler – ja, dem mit den Gesetzen der Planetenbewegung und der Sphärenharmonie. Kepler hat nämlich die bereits in der Antike studierten archimedischen Polyeder wiederentdeckt und systematisch beschrieben. Dabei entdeckte er, dass das Rhomben-Kuboktaeder durch Entecken des Rhombendodekaeders (siehe Folge 3) hergestellt werden kann. Daher das Wort "Rhomben" im Namen.

Aus dem Oktaeder macht dasselbe Verfahren – wieder ein Rhomben-Kuboktaeder! Nur die Rollen von Enteckungs-Schnittfläche und übrigbleibender Seitenfläche sind vertauscht. In der Familie der Vierzähligen, die ich Ihnen in Folge 8 vorgestellt habe, haben also Würfel und Oktaeder wieder mal ein gemeinsames Kind.

Das entsprechende Kind von Dodekaeder und Ikosaeder, also aus der Familie der Fünfzähligen, heißt Rhomben-Ikosi-Dodekaeder. (Die Bindestriche sind nicht offiziell, aber sie helfen bei diesen Bandwurmnamen schon beim Lesen, was?) Man kann ihn, wie seinen vierzähligen Vetter, auch aus einem Rhomben-Dreißigflächner heraus-entecken.

Neben dieser Standardkombination von Entkanten und Entecken gibt es eine etwas kompliziertere. Man entkante etwas weniger, sodass anstelle jeder Kante ein ziemlich langgestrecktes Sechseck übrigbleibt, und entecke dafür umso intensiver. Dabei wird nicht nur das langgestreckte Sechseck zum Quadrat zurechtgeschnitten, auch von den ursprünglichen Seitenflächen muss noch etwas mehr dran glauben, sodass aus einem (durch Entkanten ohnehin verkleinerten) n-Eck ein (2n)-Eck entsteht. Die Enteckungs-Schnittflächen sind dann auch nicht mehr k-Ecke, sondern (2k)-Ecke.

Das zugehörige Mitglied der Viererfamilie heißt "großes Rhomben-Kuboktaeder". Kepler hatte bemerkt, dass man es auch durch Entecken eines Kuboktaeders erzeugen kann – aber nur ungefähr. Wie man auch schneidet, man kriegt die Kantenlängen nicht alle gleich lang. Das entsprechende Kind aus der Fünfer-Familie heißt "großes Rhomben-Ikosi-Dodekaeder", und das macht mit 12 Zehnecken, 20 Sechsecken und 30 Quadraten schon richtig was her.

Es gibt noch zwei "Bastarde", Mitglieder, die jede Familie schamhaft verschweigt, weil sie zwar unzweifelhaft dazugehören, aber irgendwie nicht vorzeigbar erscheinen. In der Literatur heißen sie entsprechend "schiefer Würfel" (snub cube, cubus simus) und "schiefes Dodekaeder". Ich beschreibe am Beispiel des Dodekaeders, wie man sie konstruieren kann, zum Beispiel aus Karton oder den beliebten Plastik-Vielecken.

Man nehme die zwölf Fünfecke des Dodekaeders, zunächst lose, und setze an jedes von ihnen fünf gleichseitige Dreiecke an. Damit sind die Fünfeckskanten "abgesättigt" und stehen für weitere Baumaßnahmen nicht mehr zur Verfügung. Man stelle die Fünfecke ungefähr so in den Raum, wie sie für das richtige Dodekaeder stehen müssten, nur etwas weiter auseinander, und verdrehe jedes von ihnen samt anhängenden Dreiecken ein bisschen gegen den Uhrzeigersinn. Dann kommen jeweils zwei Dreiecke benachbarter Fünfecke Kante an Kante aneinander zu liegen. Man verbinde sie entlang dieser Kanten, wobei der Körper sich schon einigermaßen rundet. Nur da, wo im ursprünglichen Dodekaeder die 20 Ecken waren, gähnen jetzt noch dreieckige Löcher. Man fülle sie mit gleichseitigen Dreiecken, und fertig ist das schiefe Dodekaeder, mit zwölf Fünfecken und imposanten 80 Dreiecken.

"Schief" ist zu verstehen als "nicht spiegelsymmetrisch". In der Tat: In der Bauanleitung sind an entscheidender Stelle die Fünfecke gegen den Uhrzeigersinn zu verdrehen. Das hätte man genauso gut im Uhrzeigersinn tun können, und dann wäre das Spiegelbild des Körpers herausgekommen. Es gibt also linke und rechte schiefe Dodekaeder (desgleichen beim Würfel). Im Gegensatz zu den "richtigen" Mitgliedern der Familie sind sie also zwar symmetrisch gegen Drehungen, aber nicht gegen Spiegelungen.

Damit wird nebenbei noch etwas ganz anderes deutlich: Die Forderung "Alle Ecken sind gleich" ist zwar ziemlich stark, aber schwächer als die Forderung nach vollkommener Symmetrie. Wenn man einen der beiden schiefen Körper so um seinen Mittelpunkt verdreht, dass eine Ecke auf eine andere Ecke zu liegen kommt, dann kommt dadurch noch lange nicht der ganze Körper mit sich selbst zur Deckung.

In diesem Zusammenhang gibt es einen dritten Bastard zu erwähnen. Er ist eine Variante des Rhomben-Kuboktaeders und gilt als so missraten, dass er in den offiziellen Aufzählungen noch nicht einmal vorkommt. Schauen Sie sich das Rhomben-Kuboktaeder noch einmal scharf an. Es enthält eine "Bauchbinde" aus acht aneinanderhängenden Quadraten. Zwei weitere "Achter-Bauchbinden" verlaufen über Kopf und Fuß, aber darauf kommt es im Moment nicht an. Genau oberhalb der Bauchbinde kann man diesen Körper durch einen horizontalen Schnitt, der sämtliche Flächen heil lässt, zerteilen. Es entstehen achteckige Schnittflächen. Man drehe das obere Stück um 45 Grad und setze es auf das untere wieder auf. Das passt, denn ein verdrehtes regelmäßiges Achteck und ein unverdrehtes passen zusammen. Der so entstehende Körper hat zwar nach wie vor eine Bauchbinde (in der Abbildung weiß), aber die beiden anderen Bauchbinden sind verschwunden! Wo über der Bauchbinde ein (schwarzes) Quadrat sitzt, ist darunter ein (rotes) Dreieck, und umgekehrt. Da sind jede Menge Drehsymmetrien verlorengegangen, während kurioserweise die Spiegelsymmetrien erhalten geblieben sind.

Dieser Körper erfüllt die offizielle Definition von "archimedisch". Um jede Ecke herum liegen ein Dreieck und drei Quadrate, und sogar die Winkel zwischen benachbarten Flächen sind die richtigen. Aber er ist kein offizieller archimedischer. Manchmal sind die Geometer wirklich kleinlich.

Sie haben es vielleicht schon gemerkt: Archimedische Körper sind irgendwie Standard. Die dreizehn offiziellen sind in jedem einschlägigen Lehrbuch aufgeführt und mannigfach im Internet abgebildet. Einige Standardbücher über Polyeder allgemein habe ich in der Eröffnungsseite dieser Serie aufgeführt. Aber sind das wirklich alle, auf die die Definition passt? Nein! Es fehlen sogar noch unendlich viele. Sie sind zugegebenermaßen etwas schlicht, aber eindeutig archimedisch.

Nehmen Sie zwei regelmäßige n-Ecke und legen Sie sie, mit einem gewissen Abstand, genau übereinander. Das eine n-Eck ist der Boden und das andere die Decke eines großes Raums. Und die Wände? Die sind rechteckig, und wenn Sie den Abstand von Boden und Decke gleich der Kantenlänge des n-Ecks wählen, sind sie quadratisch. Fertig ist der Archimedische, denn er besteht aus lauter regelmäßigen Vielecken, und alle Ecken sind gleich. Er heißt das n-seitige Prisma.

Nehmen Sie jetzt die Wände wieder weg und verdrehen die Decke gegenüber dem Boden um gerade so viel, dass eine Ecke der Decke über einer Kantenmitte vom Boden zu liegen kommt und umgekehrt. Mit quadratischen Wänden ist jetzt nichts mehr zu machen – aber mit dreieckigen. Die Konstruktion funktioniert für jedes n≥3, ist archimedisch und heißt n-seitiges Antiprisma.

So ganz unbekannt sind die Prismen und Antiprismen übrigens nicht. Wenn man ein Ikosaeder oben und unten köpft, sprich ihm einen Punkt samt den fünf daran angrenzenden Dreiecken wegschneidet und mit dem gegenüberliegenden Punkt ebenso verfährt, bleibt ein fünfseitiges Antiprisma übrig. Das dreiseitige Antiprisma ist besser bekannt unter dem Namen Oktaeder, und das vierseitige Prisma ist nichts anderes als der biedere Würfel. Sicher: Die platonischen Körper fallen alle unter die Definition von archimedisch, aber die sind ja ohnehin etwas Besseres und würden sich beschweren, dazugezählt zu werden.

Speziell für die archimedischen Körper hält Douglas Zongker einen kompletten Satz Bildchen und mehrfarbige Bastelbögen zum Download bereit.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft