In der letzten Folge hatte ich Ihnen das Rhombendodekaeder einerseits und den Oktaederstumpf andererseits vorgestellt. Beide sind Raumfüller, das heißt, mit vielen Exemplaren eines solchen Körpers lässt sich der Raum lückenlos voll stapeln. Beide lassen sich als Voronoi-Zellen ("Vorgärten") eines Kristallgitters interpretieren. Man stapele den Raum mit gewöhnlichen Würfeln voll, nehme die Mittel- und Eckpunkte aller Würfel (für den Oktaederstumpf) oder auch nur die Mittelpunkte aller weißen Würfel in einer Schwarzweiß-Schachbrett-Würfelpackung (für das Rhombendodekaeder) und lasse die so ausgewählten Gitterpunkte sich um den Platz prügeln. Das läuft darauf hinaus, dass jeder Gitterpunkt alles um sich herum für sich kriegt, was ihm näher liegt als jedem anderen Gitterpunkt. Das ist der Vorgarten dieses Punktes.

Nachdem die beiden Kristallgitter eng miteinander verwandt sind, sollten ja auch die beiden Vorgartenkörper etwas miteinander zu tun haben. Das ist in der Tat der Fall. Wahrscheinlich gibt unter den Kristallographen Fachleute, die das auch wissen; aber sie sagen es nicht so laut. Jedenfalls weiß ich es nicht aus einem Lehrbuch, sondern bin darauf gestoßen, als ich bei einer Führung im Mathematischen Institut der Universität Göttingen ein paar merkwürdige Gipsklötzchen zu sehen bekam.

Die Klötzchen stehen dort in einer Vitrine und gehen auf Arthur Schoenflies (1853 – 1928) zurück. Schoenflies ist als "Vater der Kristallographie" berühmt geworden. Eine heute noch viel verwendete Einteilung der Kristalle in Klassen geht auf ihn zurück.

Professor Samuel Patterson, der die Führung durchführte, erzählte mir, die Klötzchen seien, wahrscheinlich auf Geheiß von Schoenflies, von einer Firma namens Schilling hergestellt worden und auch in deren "Catalog mathematischer Modelle" (Halle 1902) aufgeführt gewesen. Was Schoenflies selbst damit im Sinn hatte, müsste seinen Werken zu entnehmen sein. Nur sind die leider sehr umfangreich. Herr Patterson hat keinen Hinweis gefunden, ich auch nicht. Natürlich habe ich die Texte nicht Wort für Wort studiert ... Wer möchte, findet in den dreiteiligen "Abhandlungen über Translationsgruppen" (Mathematische Annalen Band 28, 29 und 34) sowie den Büchern "Krystallsysteme und Krystallstructur" (Leipzig 1891) sowie "Theorie der Kristallstruktur" (1923) reichlich Beschäftigung. Aber auch so bin ich für jeden Hinweis dankbar.

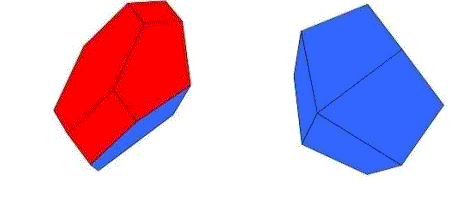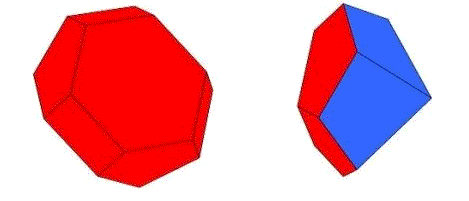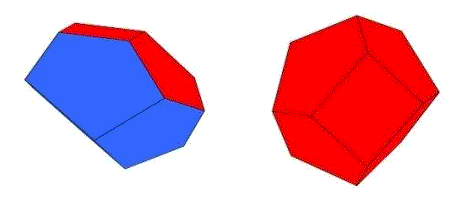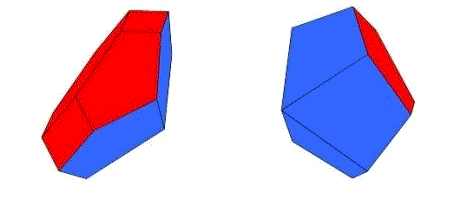
Hier sind die Helden der Geschichte. Die Oberflächen habe ich rot und blau eingefärbt, damit es hinterher schöner aussieht. Ich nenne sie den flachen und den spitzen Schoenflies und hoffe, dass der große Meister mir die respektlose Bezeichnung nicht übel nehmen würde.

Bei genauerem Hinsehen stellt sich heraus, dass bei beiden Klötzen der rote Teil der Oberfläche ein Stück vom Oktaederstumpf ist. Beim flachen Schönflies ist es ein Sechseck mit drei halben Quadraten und drei drittel Sechsecken dran, beim spitzen Schoenflies ein Quadrat mit vier drittel Sechsecken. Dagegen gehören die blauen Teile der Oberfläche zu einem Rhombendodekaeder. Beim flachen Schoenflies ist es die Umgebung einer stumpfen Ecke und beim spitzen die Umgebung einer spitzen Ecke.

Mehr noch: Es gibt verschiedene Möglichkeiten, die beiden Raumfüller Oktaederstumpf und Rhombendodekaeder aus den Klötzen zusammenzusetzen. Man füge vier flache Schoenfliese mit den blauen Seiten aneinander, und es entsteht ein Oktaederstumpf!

Andersherum betrachtet: Wenn man einen Oktaederstumpf durch ebene Schnitte, die bis zum Mittelpunkt reichen, so raffiniert zersägt, dass die Quadrate entlang einer Mittelinie geteilt werden, dann erhält man vier flache Schoenfliese. Aber dieser Zerteilungsakt hat die Symmetrie des Oktaederstumpfs gebrochen. Man hätte die Quadrate ja auch alle entlang der jeweils anderen Mittellinie halbieren können, und dann hätte die Säge von den sechs Seiten des Sechsecks die drei anderen Seiten zerlegt und die zuvor zersägten heil gelassen.

Eigentlich hat der Oktaederstumpf die Symmetrie des Würfels (oder des Oktaeders, was dasselbe ist), das heißt, alle die Drehungen und Spiegelungen, die den Würfel in sich selbst überführen, lassen auch den Oktaederstumpf unverändert. Nach der Zersägung ist davon nur noch die Symmetrie des Tetraeders übrig geblieben.

Wenn man sechs spitze Schoenfliese mit den blauen Seiten aneinander setzt, entsteht ebenfalls ein Oktaederstumpf; diesmal ohne Symmetriebrechung.

Nichts hindert einen, mit den so zusammengesetzten Oktaederstümpfen den Raum irgendwie voll zu stopfen. Aber das ist uncool. Es soll ja schon irgendwie regelmäßig sein.

Eine Möglichkeit, es regelmäßig zu tun, geht so: Man nehme einen Oktaederstumpf (es kommt nicht darauf an, wie er zusammengesetzt ist), setze auf seine sechseckigen Flächen flache Schönfliese und auf seine quadratischen Flächen spitze Schoenfliese. Siehe da, es entsteht ein ziemlich großes Rhombendodekaeder!

Und da dieses ein Raumfüller ist, darf man diese Struktur beliebig oft wiederholen. An den spitzen Ecken der Rhombendodekaeder-Raumfüllung entstehen Oktaederstümpfe aus sechs spitzen Schoenfliesen, an den stumpfen Ecken entstehen Oktaederstümpfe aus vier flachen Schoenfliesen, mit anderen Worten: Die Raumfüllung durch Oktaederstümpfe wird durch diese Konstruktion in einem Aufwasch mit erzeugt.

Nur in dem Oktaederstumpf, mit dem wir angefangen haben und der jetzt in der Mitte des Rhombendodekaeders sitzt, steckt noch jede Menge Willkür. Drei Anordnungen kommen in Frage: sechs spitze Schoenfliese, vier flache sorum und vier flache andersrum. Ob sich durch geschickte Wahl dieser Anordnungen noch mehr interessante Strukturen herstellen lassen? Ob Schoenflies sich etwas Spezielles dabei gedacht hat? Ob Paare von Klötzen, geeignet zusammengefügt, als Raumfüller oder ähnliches dienen können? In der Vitrine in Göttingen stehen einige solcher Paare.

Vielleicht machen Sie noch bedeutende Entdeckungen, wenn Sie sich ein ausreichendes Sortiment von Schoenfliesen zusammenbasteln und damit spielen. Eine Bastelanleitung samt vorbereiteten Bastelbögen finden Sie weiter unten.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft