In der letzten Folge habe ich – als Beispiel – das Dodekaeder ziemlich auseinander genommen, um daran seine Symmetriegruppe zu erläutern. Dabei ließ sich ein kleiner Abstecher in die allgemeine Gruppentheorie nicht ganz vermeiden. Am Ende hatten wir das Werkzeug beisammen, um schön formal und algebraisch zu beschreiben, was die Symmetrie – zum Beispiel – eines platonischen Körpers bedeutet. Diesmal wollen wir das Werkzeug wenigstens zaghaft anwenden, um damit ein großes Sortiment symmetrischer Körper zu erzeugen.

Wie war das? Symmetrie ist, wenn man das Ding irgendwie bewegen kann, und hinterher sieht es trotzdem genauso aus wie zuvor. Etwas ordentlicher formuliert: Man erfasst die Symmetrie eines Körpers, indem man sämtliche Kongruenzabbildungen (Verschiebungen, Drehungen, Spiegelungen) aufzählt, unter denen der Körper unverändert ("invariant") bleibt. Diese Abbildungen heißen dann Symmetrietransformationen oder (kurz und manchmal etwas verwirrend) Symmetrien dieses Körpers.

Über die Verschiebungen brauchen wir nicht groß nachzudenken; denn um unter einer Verschiebung invariant zu sein, müsste das Gebilde schon unendlich ausgedehnt sein. Vielmehr geht es um Drehungen und Spiegelungen, die sämtlich einen bestimmten Punkt (den Mittelpunkt des Körpers) unverändert lassen.

Für das Dodekaeder, das Ikosaeder oder irgendeinen ihrer nahen Verwandten gibt es genau 120 solcher Symmetrien: Die ganze Familie dieser Körper (der "Fünfzähligen") ist dadurch charakterisiert, dass jedes Familienmitglied allen 120 Symmetrien gegenüber invariant ist. Eine Kombination von zwei dieser Abbildungen – erst die eine anwenden, dann die andere – ergibt wieder eine Abbildung aus der Menge, weswegen sie "Gruppe" heißt, in diesem Fall die "Symmetriegruppe des Ikosaeders". Zu den 120 Gruppenelementen zählen die Spiegelungen an den 15 Symmetrieebenen sowie deren Kombinationen, darunter insbesondere Drehungen um gewisse Achsen um ein Fünftel, ein Drittel oder auch die Hälfte des Vollwinkels. Der Vollständigkeit halber zählt Nichtstun (die "identische Abbildung" oder auch "das neutrale Element der Gruppe") auch dazu.

Die anderen platonischen Körper haben Symmetriegruppen, die im Detail ganz anders, aber im Prinzip ähnlich gebaut sind wie die Symmetriegruppe des Ikosaeders; diese soll auch für das Folgende wieder als Leitbeispiel dienen.

Diesmal soll es also weniger ums Auseinandernehmen gehen als ums Zusammensetzen. Wie konstruiert man möglichst viele Körper, die zur Familie gehören?

Dazu fangen wir wieder bei Urvater und Urmutter (Dodekaeder und Ikosaeder) an. Setzen wir sie abermals so ineinander, dass die Dualität am schönsten zum Ausdruck kommt, das heißt so, dass stets eine Kante vom einen Körper und eine vom anderen Körper einander halbieren und aufeinander senkrecht stehen. Insbesondere fallen ihre beiden Mittelpunkte zusammen. Denken wir uns die Körper als Kantenmodelle, packen sie beide gemeinsam in eine große Hohlkugel aus Milchglas mit demselben Mittelpunkt und setzen in diesen Mittelpunkt eine punktförmige Glühbirne. (Solche Lampen hatten wir früher in der Schule, mit nicht-punktförmigen Glühbirnen natürlich.)

Dann zeichnen sich die Schatten der Kanten auf der Kugeloberfläche ab. Aus den ebenen Fünfecken des Dodekaeders werden gleichseitige, gleichwinklige Kugelfünfecke mit Innenwinkeln von 120 Grad statt 108 Grad bei den ebenen Fünfecken. Wieso 120 Grad? Na ja, es treffen sich in jedem Eckpunkt drei gleiche Kugelfünfecke, die müssen sich die 360 Grad gleichmäßig aufteilen, das macht 120 Grad für jeden. Und wieso sind das mehr als beim ebenen Fünfeck? Na ja, weil bei der Projektion auf die Kugeloberfläche die Kanten in der Mitte ausgebeult werden und sich dadurch unter anderen Winkeln treffen als zuvor.

Beim Schatten des Ikosaeders fällt das noch mehr auf. Aus dessen Flächen werden Kugeldreiecke, die liegen zu fünft um einen Punkt, also haben sie lauter Innenwinkel von 72 Grad, das macht im einzelnen Dreieck eine Winkelsumme von 3 x 72 = 216 Grad. Daran muss man sich auf der Kugel gewöhnen: Die Winkelsumme im Dreieck ist stets größer als die aus der Ebene gewohnten 180 Grad, und der Überschuss (der "sphärische Exzess") ist umso größer, je größer die Fläche des Dreiecks selbst ist.

Sind denn die Winkel im Kugeldreieck überhaupt vernünftig definiert, wo doch die Seiten krumme Linien sind? Das ist kein Problem. Der Winkel zwischen zwei krummen Linien ist der Winkel zwischen ihren Tangenten.

Es dürfen übrigens auf der Kugel nicht irgendwelche krummen Linien sein. Was in der Ebene die Geraden sind, das sind in der Kugelgeometrie die so genannten Großkreise: Kreise, deren Mittelpunkt mit dem Kugelmittelpunkt zusammenfällt, so wie das auf der Erde für den Äquator und für alle Längengrad-Kreise gilt, nicht jedoch für die Breitenkreise (außer dem Äquator). Ein Geradenstück, zum Beispiel eine Polyederkante, das mit einer punktförmigen Glühbirne im Kugelmittelpunkt beleuchtet wird, wirft auf der Milchglas-Kugeloberfläche einen Schatten in Form eines Großkreisstücks.

Und wozu machen wir uns überhaupt die Mühe mit diesem krummen Gebilde namens Kugel, wo doch die Verhältnisse in der Ebene viel übersichtlicher sind? Damit es einfacher ist. Wir werden gleich die Oberfläche der Kugel in irgendwelche Vielecke zerlegen; wenn wir damit fertig sind, hindert uns nichts daran, die Eckpunkte einer solchen Zerlegung durch gerade statt durch krumme Kanten zu verbinden, und schon haben wir ein schönes Polyeder. (Na ja, es könnte passieren, dass zum Beispiel vier Eckpunkte eines Kugelvierecks nicht in einer Ebene liegen; da muss man dann schon aufpassen.) Von der Kugel zum Polyeder zurückzukehren ist also nicht schwer; aber jetzt nehmen wir erstmal unser duales Paar von Ikosaeder und Dodekaeder, beleuchten die beiden mit der punktförmigen Mittelpunkts-Glühbirne und schauen uns die Schatten auf der Kugel an. Und siehe da: Die liegen alle auf relativ wenigen Großkreisen. Beispiel: Der Schatten einer Dodekaederkante, verlängert, teilt ein benachbartes Fünfeck genau in der Mitte, geht also auch durch dessen Mittelpunkt. Der ist aber – in der Projektion auf die Kugel – dasselbe wie ein Eckpunkt des Ikosaeders. Von dem gehen fünf Kanten aus, darunter eine, die senkrecht und mittig auf einer Fünfecksseite steht. Genau dasselbe gilt für die Verlängerung unserer Dodekaederkante auch, also liegen die Kanten beider Körper auf ein und demselben Großkreis, und während der die Runde um die Kugel macht, kommt noch ein Paar Kanten dazu.

Insgesamt gibt es fünfzehn solcher Großkreise. Was Wunder: Die Ebenen dieser Großkreise sind genau die fünfzehn Symmetrieebenen, mit denen wir unsere Gruppe aufgebaut haben. Die Großkreise treffen sich zu fünft in den Eckpunkten des Ikosaeders, zu dritt in den Flächenmittelpunkten des Ikosaeders (oder auch den Ecken des Dodekaeders, was dank Projektion auf die Kugel dasselbe ist) und zu zweit in den Kantenmittelpunkten, was ja für die beiden Körper dieselben Punkte sind. Und diese Schnittpunkte sind genau die "Drehpunkte", das heißt die Punkte, in denen unsere 31 Drehachsen die Kugeloberfläche durchstoßen.

Alle Großkreise zusammengenommen zerlegen die Kugeloberfläche in lauter rechtwinklige Dreiecke. Deren Eckpunkte sind:
A: ein zweizähliger Drehpunkt, zugleich gemeinsamer Kantenmittelpunkt von Ikosaeder und Dodekaeder, projiziert auf die Kugeloberfläche, mit rechtem Winkel;
B: ein dreizähliger Drehpunkt, Eckpunkt vom Dodekaeder, Flächenmittelpunkt vom Ikosaeder (jeweils projiziert natürlich), mit Winkel 60 Grad; und
C: ein fünfzähliger Drehpunkt, Eckpunkt vom Ikosaeder, Flächenmittelpunkt vom Dodekaeder, mit Winkel 36 Grad. Die Winkelsumme ist mit 186 Grad etwas größer als die gewohnte, wie sich das auf der Kugel gehört.

Ein Dodekaeder-Fünfeck besteht aus zehn solchen Dreiecken, und zwar gruppieren sich abwechselnd rechte und linke um den Fünfecksmittelpunkt. Entsprechend besteht ein Ikosaeder-Dreieck aus sechs solchen Dreiecken. (Genau genommen muss man wieder von der Kugel auf das jeweilige Polyeder herunterprojizieren.) Wie man es auch zählt, 10 x 12 oder 6 x 20: Es sind insgesamt 120 Dreiecke, genau so viele, wie unsere Symmetriegruppe Elemente hat. Das kann doch kein Zufall sein.

Ist es auch nicht. Greifen wir uns ein solches Dreieck heraus und spiegeln es an einer seiner Seiten (genauer: an der Symmetrieebene, die durch diese Dreiecksseite geht). Dann kommt genau das an diese Seite angrenzende Nachbardreieck heraus! So sind die Dreiecke ja gerade definiert, dass ihre Seiten in Symmetrieebenen liegen. Das Spiel geht weiter: Wenn man auf unser Musterdreieck alle 120 Abbildungen der Symmetriegruppe anwendet, ergeben sich alle 120 Dreiecke, sodass die gesamte Kugel bedeckt ist.

Unser Dreieck heißt ein "Fundamentalbereich" der Ikosaedergruppe; und für diesen Begriff ist ein kurzer Abstecher in die Welt der Tapetenmuster und Badezimmerkacheln angesagt.

Gemeint sind zweidimensionale Muster, die sich in zwei verschiedenen Richtungen beliebig oft wiederholen. Das heißt, es gibt zwei nicht-parallele Vektoren, und wenn man das Muster entlang einem der Vektoren verschiebt, kommt es wieder mit sich selbst zur Deckung. Mit unseren frischen Gruppentheorie-Kenntnissen können wir das auch so ausdrücken: Die Symmetriegruppe des Musters besteht aus unendlich vielen Elementen, nämlich den Parallelverschiebungen (Translationen) um n-mal den einen Vektor plus k-mal den anderen Vektor; dabei sind n und k beliebige (positive oder negative) ganze Zahlen. Gegenüber allen Elementen dieser Gruppe ist das Muster (das wir uns unendlich ausgedehnt vorstellen) nämlich invariant.

Schauen wir uns das Parallelogramm an, das von unseren beiden Verschiebungsvektoren aufgespannt wird. Das ist nämlich ein Fundamentalbereich der Symmetriegruppe, das heißt, wenn man alle Abbildungen der Gruppe auf ihn anwendet, bedecken die Bilder die ganze Welt (hier also die Ebene) lückenlos, ohne sich zu überlappen, außer allenfalls an den Rändern, wo man ein bisschen aufpassen muss.

Das heißt aber auch: Wenn man das Muster innerhalb des Fundamentalbereichs kennt, kennt man es in der ganzen Welt. Eine Festlegung des Musters in dem unschuldigen kleinen Parallelogramm, und schon ist es überall festgelegt. Das machen sich die Kristallografen zunutze. Ein Kristall ist nämlich eine Anordnung von Atomen, die nicht nur in zwei, sondern in drei Raumrichtungen periodisch ist. Entsprechend ist der Fundamentalbereich eines Kristalls ein Parallelepiped: das, was von drei (Verschiebungs-)Vektoren, die nicht in einer Ebene liegen, aufgespannt wird. Wenn diese Vektoren senkrecht aufeinander stehen, ist es ein Quader, und im allgemeinen Fall halt ein verzerrter Quader, mit nach wie vor parallelen Seitenflächen. Kennt man die Positionen der Atome in einem Fundamentalbereich, so kennt man sie im ganzen Kristall.

Zu einem gegebenen Muster (oder Kristall) gibt es stets viele verschiedene (und auch verschieden geformte) Bereiche, die als Fundamentalbereiche fungieren können; natürlich wählt man den, der für die Anschauung oder das Rechnen am bequemsten ist.

Zurück zur Kugel und ihrer Pflasterung durch die 120 kleinen Fundamental-Dreiecke. (Man könnte die Dreiecke in der Tat durch wesentlich wildere Gebiete ersetzen, aber das bringt überhaupt nichts: Der Vorteil, der dadurch entsteht, dass man an den Rändern des Fundamentalbereichs spiegeln kann, ist praktisch nicht zu schlagen.) Wir wissen jetzt: Ein Polyeder aus der Familie der Fünfzähligen ist bereits dadurch festgelegt, was in einem solchen Fundamentaldreieck passiert. Beispiel: Ich wähle einen Punkt in diesem Dreieck aus und ernenne ihn zum Eckpunkt meines Polyeders. Schon habe ich, dank Symmetriegruppe, 120 Eckpunkte am Hals. Sagen wir, dass die Kanten jeweils zwischen einem Punkt und dessen Bildpunkt im Nachbardreieck verlaufen sollen: Dann ist das Polyeder schon fertig.

Na ja, fast. Wir müssen ja noch von der Kugeloberfläche auf die ebenen Begrenzungsflächen des Polyeders herunterprojizieren, und dabei könnte es theoretisch passieren, dass aus einem von Kanten umschlossenen Gebiet auf der Kugel nicht ein ebenes Vieleck, sondern ein irgendwie windschiefes Gebilde wird. Diese Möglichkeit ist durch ein paar Zusatzüberlegungen auszuschließen.

Somit hätte jedes Polyeder aus der Familie der Fünfzähligen mindestens 120 Eckpunkte? Nicht ganz. Ich darf ja meinen ausgewählten Punkt auch auf eine Seite oder in eine Ecke des Fundamentaldreiecks legen. Dann fällt er mit einem oder mehreren seiner Spiegelbilder zusammen, wodurch sich die Anzahl der Eckpunkte drastisch vermindert. Insbesondere erhalte ich das Dodekaeder (Ikosaeder) zurück, wenn mein ausgewählter Punkt der Eckpunkt B (C) des Fundamentaldreiecks ist; in diesem Fall fallen jeweils 6 (10) Eckpunkte in einen zusammen.

Wenn der ausgewählte Punkt auf dem Dreieck umherwandert, verwandelt das durch ihn definierte Polyeder sich mit, wobei alles säuberlich in der Familie bleibt. So erhält man auf einfache Weise einen stetigen Übergang zwischen Ikosaeder und Dodekaeder, und noch einiges mehr.

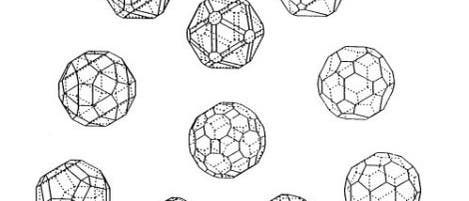
Der Basler Mathematiker Renatus Ziegler hat während seiner Arbeit an der Mathematisch-Astronomischen Sektion des Goetheanums (der Forschungsstätte der Anthroposophen) in Dornach (Schweiz) diese stetigen Übergänge in zahlreichen Bildern ausgearbeitet. Die Bilder auf dieser und der vorigen Seite sind, mit seiner freundlichen Genehmigung, sämtlich seinem Buch "Morphologie von Kristallformen und symmetrischen Polyedern" entnommen.

Ziegler ordnet die durch diese Konstruktion entstehenden Polyeder im Dreieck an – im Fundamentaldreieck, und zwar jedes Polyeder an den Punkt, der es definiert. So sitzt das Ikosaeder auf Ecke C des Fundamentaldreiecks, der fünfzähligen. Der zugehörige Punkt ist sozusagen zehnfach besetzt, von dem Punkt selbst und seinen neun Kollegen aus den Nachbardreiecken. So kommt das Ikosaeder an seine zwölf (statt 120) Eckpunkte. Das Dodekaeder sitzt auf der (dreizähligen) Ecke B. Dass alle 120 Ecken auseinanderfallen, kommt an den Ecken und den Rändern des Fundamentaldreiecks nicht vor; nur im Inneren entfaltet sich die volle Pracht (Bild 1).

Der ausgewählte Punkt im Fundamentaldreieck muss nicht unbedingt ein Eckpunkt sein. Man kann in diesem Punkt auch einfach eine Tangentialebene an die Kugel legen. Wo diese 120 Ebenen (oder entsprechend weniger, wenn wieder Bild und Spiegelbild zusammenfallen) sich schneiden, sind die Kanten des dadurch definierten Polyeders. Dieses Polyeder ist dual zu demjenigen, wo der ausgewählte Punkt Eckpunkt ist; denn aus Eckpunkt wird Fläche, wie bei der Dualität üblich (Bild 2).

Einmal eingeführt, erlaubt das Prinzip die verschiedensten Variationen: Statt der vollen Ikosaedergruppe kann man die Drehgruppe wählen, die keine reinen Spiegelungen, sondern nur orientierungserhaltende Abbildungen enthält (für Einzelheiten siehe die letzte Folge). Ein Fundamentalbereich der Drehgruppe besteht aus einem Paar benachbarter Fundamentaldreiecke der vollen Ikosaedergruppe. Statt 120 Bildpunkte gibt es nur noch 60 bzw. entsprechend weniger, und auf diesem Wege erzeugt man die schiefen Verwandten der Fünfzähligen (Bild 3). Wirklich schief sind sie allerdings nur, wenn der erzeugende Punkt im Inneren des Fundamentaldreiecks liegt. Wenn er auf dem Rand liegt, ist er gleich seinem eigenen Spiegelbild; das gilt dann auch für das von ihm erzeugte Polyeder.

Oder dasselbe wieder mit Tangentialebenen statt Eckpunkten (Bild 4).

Und natürlich ist man nicht darauf beschränkt, nur einen Punkt in den Fundamentalbereich zu setzen. Man ist frei, über dem Stück Kugeloberfläche ein ganzes, beliebig zerklüftetes Gebirge zu errichten. Das wird mitsamt seinen automatisch erzeugten Spiegelbildern die ganze (Erd-)Kugel bedecken, und wenn es aus ebenen Flächen bestand, ergibt sich auf diese Weise ein Polyeder. Die archimedischen Körper, Stewarts Hohlkörper, … die kompletten Polyederfamilien lassen sich auf diesem Wege gewinnen, und zwar auf sehr ökonomische Weise. Es genügt, den Fundamentalbereich zu bebauen; alles andere erledigt die Symmetriegruppe. Denn alles bisher Besprochene funktioniert genauso mit der Oktaeder- und der Tetraedergruppe.

Auf den ersten Blick scheint letztere kaum Neues zu bieten. Wie auch: Es ist ja eine Untergruppe der Oktaedergruppe, hat also nur halb so viele Symmetrien. Wir wissen inzwischen: Wenn unser ausgezeichneter Punkt auf dem Rand oder gar in einer Ecke des Fundamentaldreiecks liegt, gibt das zusätzliche Symmetrien. So sollten wir uns vielleicht nicht wundern, wenn die Tetraedergruppe in Punkt C das Oktaeder (Punktform) bzw. den Würfel (Flächenform) liefert, ebenso wie die große Schwester Oktaedergruppe.

Aber dann bringt die so mager ausgestattete Tetraedergruppe doch noch eine Überraschung. Mitten auf dem rechten Rand des Dreiecks, halbwegs zwischen Oktaeder und Kuboktaeder, findet sich das Ikosaeder! In der Punktform (Bild 5). In der Flächenform (Bild 6) ist es ebenso überraschend das Dodekaeder zwischen Würfel und Rhombendodekaeder.

Wie kann das sein? Das ist doch die falsche Familie, oder? Nicht wirklich. Die Tetraederfamilie ist sehr umfassend. Sowohl die Vierzähligen als auch die Fünfzähligen sind außerdem auch dreizählig, auch wenn man das nicht zu erwähnen pflegt. Das Dodekaeder hat auch die Symmetrie des Tetraeders. Deswegen sind diese Durchdringungskörper, wie zum Beispiel fünf Tetraeder in einem Dodekaeder, ja so ansehnlich (siehe Folge 12 "Durchdringungen"). Hier also, in der Primitivform des Tetraeders, steckt der "gemeinsame" Vorfahr dieser beiden so verschiedenen Familien.

Kommentare und Anregungen sind wie immer stets willkommen!

Herzlich Ihr

Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft

Literaturhinweise zu dieser Folge:
Renatus Ziegler: Morphologie von Kristallformen und symmetrischen Polyedern. Verlag am Goetheanum, Dornach 1998.