Räumliche Geometrie: Körper aus lauter Dreiecken
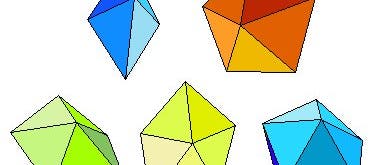
Konvexe Dreieckskörper
Wie viele Körper gibt es, die ausschließlich von gleichseitigen, gleich großen Dreiecken berandet werden?
Na ja, unter den platonischen Körpern gibt es drei, für die das gilt: das Tetraeder, das Oktaeder und das Ikosaeder. Das müsste dann doch eigentlich alles gewesen sein, denn weitere platonische Körper gibt es nicht.
Schon richtig – aber die Forderungen an einen platonischen Körper sind auch sehr streng. Nicht nur alle Flächen müssen gleich (und reguläre Vielecke) sein, sondern auch alle Ecken, sprich: In jeder Ecke müssen sich gleich viele Flächen treffen, und auch die Winkel zwischen den Flächen müssen rund um jede Ecke dieselbe Folge bilden.
Besteht man nicht mehr auf der Forderung, dass alle Ecken gleich sein müssen, dann kommen zu den bekannten drei platonischen Körpern zunächst noch fünf dazu. Im Englischen heißen sie Deltahedra, und Eric Weissteins sehr reichhaltiges Online-Mathematik-Lexikon führt sie alle auf.
Wie sind die fünf neuen Dreieckskörper gebaut? Am besten legt man sich in der Vorstellung ein paar Bausteine zurecht: einen Dreierhut, das ist ein Tetraeder, dem eine Fläche fehlt; einen Viererhut, das ist eine vierseitige Pyramide ohne Grundfläche oder auch ein halbes Oktaeder; und einen Fünferhut, das ist eine fünfseitige Pyramide ohne Grundfläche, und man findet sie als Bestandteil des Ikosaeders. Stellen Sie sich so ein Ikosaeder auf einer Ecke stehend vor. Dann können Sie mit zwei horizontalen Schnitten einen Fünferhut oben abschneiden und einen kopfstehenden Fünferhut unten. Übrig bleiben zwei fünfeckige, horizontale Schnittflächen, die gegeneinander verdreht sind: Ein Eckpunkt des oberen Fünfecks steht über der Seitenmitte des unteren und umgekehrt. Dazwischen liegt das, was man ein "Antiprisma" nennt: Kanten verbinden im Zickzack die Ecken des oberen und des unteren Fünfecks. Daraus entstehen die zehn übrigen Dreiecke des Ikosaeders.
Man kann nun das fünfseitige Antiprisma aus dem Ikosaeder herausschneiden und den oberen Fünferhut direkt (nur ein bisschen verdreht) auf den unteren aufsetzen. Das gibt schon einen der neuen Körper (10 Flächen). Zwei Dreierhüte mit den Öffnungen aufeinander setzen gibt den nächsten (6 Flächen). Zwei Tetraeder aufeinander zu setzen läuft auf dasselbe hinaus.
Zwei Viererhüte aufeinander gibt nichts Neues, sondern nur das wohlbekannte Oktaeder. Aber man kann das Umgekehrte machen wie beim Ikosaeder: Zwischen die beiden Viererhüte setze man ein vierseitiges Antiprisma. Macht zusammen 16 Flächen.
Oder man nehme ein dreiseitiges Prisma (Boden und Deckel sind gleichseitige Dreiecke, die Seitenwände Quadrate) und setze auf jede Seitenwand einen Viererhut auf. Das gibt einen Körper aus insgesamt 14 Flächen.
Der letzte unter den fünf neuen Dreieckskörpern ist der verrückteste. Ich stelle ihn mir am liebsten aus dem doppelten Fünferhut (dem Zehnflächner von oben) entstanden vor. Wenn man den aus Karton bastelt, verklebt man ja die beiden Fünferhüte an fünf Kanten miteinander. Von diesen lasse ich jetzt zwei benachbarte Kanten ungeklebt. Dadurch wird das ganze Gebilde beweglich. Wenn man es so zusammendrückt, dass sich der Schlitz öffnet, tut sich ein großes Froschmaul auf, und wenn es die richtige Größe hat, kann man es mit zwei weiteren gleichseitigen Dreiecken genau wieder verschließen. Das fertige Gebilde (mit 12 Flächen) ist sogar ein bisschen symmetrischer, als aus dieser Beschreibung hervorgeht: Das gestopfte Froschmaul sieht nämlich, bis auf eine Drehung um 90 Grad, genauso aus wie der Hintern vom Frosch.
Insgesamt sind damit fast alle geraden Flächenanzahlen von 4 bis 20 unter den Dreieckskörpern vertreten. Nur ein Dreiecks-Achtzehnflächner ist nicht dabei.
Nichtkonvexe Dreieckskörper
Das ist aber nur ein verschwindend geringer Teil aller Dreieckskörper überhaupt. Die bisher aufgeführten sind sämtlich konvex, das heißt, sie haben keine einspringenden Ecken. Die offizielle Definition ist: Eine Menge heißt konvex, wenn sie zu je zwei ihrer Punkte auch die gesamte Verbindungsstrecke dieser Punkte enthält. Für Polyeder, also Teilmengen des Raums, die von ebenen Flächen begrenzt werden, kann man den Begriff auch anders fassen: Ein Polyeder ist konvex, wenn man durch jede seiner Ecken eine Ebene legen kann, die das Polyeder nur in dieser Ecke trifft und sonst nirgends. Eine Ecke, für die es keine solche Ebene gibt, ist eine einspringende Ecke.
Wenn man nun die Bedingung, dass der Körper konvex sein soll, fallen lässt, gibt es kein Halten mehr. Es gibt unendlich viele Körper, die ausschließlich von gleichseitigen Dreiecken begrenzt werden. Dabei sind die "gerade noch konvexen" Körper, bei denen mehrere Dreiecke in einer Ebene liegen, noch gar nicht mitgezählt.
Fangen wir mit den einfachsten und regelmäßigsten an. Auf einen platonischen Körper Dreier-, Vierer- oder Fünferhüte aufsetzen geht immer. Aus dem Tetraeder wird die "Stella octangula", die wir schon als Durchdringungskörper zweier (großer) Tetraeder kennen gelernt haben. Die anderen Körper dieser Bauart sehen nicht besonders hübsch aus – stachlig halt, aber nicht richtig, eher wie leicht zurückgebliebene Weihnachtssterne mit unterentwickelten Spitzen.
Beim Dodekaeder tut sich eine neue Möglichkeit auf. Dieser Körper ist nämlich so dick, dass man die Hütchen einwärts statt auswärts setzen kann, ohne dass sie sich im Inneren des Körpers in die Quere kommen. Das ist ein Körper aus 60 Dreiecken, der schon wieder ganz hübsch aussieht (Bild).
Oder man nimmt den Körper, der aus einem Dodekaeder entsteht, dem man an jeder Ecke ein Dreieck wegschneidet, sodass von jedem Fünfeck nur ein kleineres Fünfeck übrigbleibt. Es sieht dann ganz gut aus, wenn man jedes dieser kleineren Fünfecke durch ein einwärts gerichtetes Fünferhütchen ersetzt. Das Ding besteht aus immerhin 80 gleichseitigen Dreiecken (Bild)!
An diesen Beispielen kann man sich durch scharfes Hinschauen klarmachen, dass in der Tat nicht alle Ecken gleich sind. Es gibt Ecken, in denen treffen sich fünf Dreiecke – wie beim Ikosaeder, bloß einwärts statt auswärts – und andere, da treffen sich sechse. Der letztere Umstand erfreut übrigens den Bastler: Sechs gleichseitige Dreiecke um einen Punkt, das ist wie in der Ebene, und deswegen kann man das, was einer solchen Ecke benachbart ist, ohne Schneiden und Kleben, nur durch geeignetes "Zerknittern", aus einem einzigen Stück Karton herstellen. Das geht so weit, dass der ganze Achtzigflächner aus einem einzigen Stück Karton gefertigt ist.
Die Oktaederkuppel
Das Spiel geht natürlich beliebig weiter: Nachdem man einen Körper durch Hütchen erweitert hat, kann man auf jedes Dreieck eines Hütchens ein weiteres Hütchen aufsetzen, jedenfalls solange noch Platz ist, und weiter Hütchen auf Hütchen.
Ein Dreierhütchen aufsetzen ist dasselbe wie ein Tetraeder aufsetzen (der einzige Unterschied zwischen Dreierhütchen und Tetraeder verschwindet im Inneren des neu entstehenden Polyeders). In der Tat kann man aus Tetraedern beliebig lange und krumme Würste machen, und aus Oktaedern und Ikosaedern ebenso.
Das ist ganz nett, und die Kristallographen bringen sogar ein gewisses (begrenztes) Interesse dafür auf. Immerhin ist ein Kohlenstoffatom mit seinen vier Valenzen so etwas wie ein Tetraeder. Die vier äußersten Elektronen können sich nämlich eigentlich nicht ausstehen und würden am liebsten Tetraederformation annehmen, weil sie da am weitesten auseinander sind. Nur: Wenn sich viele Kohlenstoffatome zusammenschließen, dann rücken die Elektronen an manchen Stellen der Bindung etwas enger zusammen, weil sie sich in der Bindung wohler fühlen als lose und dafür sogar die gegenseitige Abneigung ein bisschen überwinden. Schon ist das Tetraeder verzerrt, und deswegen ist das Interesse der Kristallographen an Tetraederwürsten auch begrenzt.
Die Geometer andererseits lieben die Polyederwürste aller Art auch nicht so besonders, und zwar wegen ihrer Beliebigkeit. Besonders ansehnlich sind sie nicht, irgendwelche bedeutenden Regelmäßigkeiten und Symmetrien gibt es auch nicht – es sei denn, es gelingt, zum Beispiel eine Wurst zu einem Ring zu schließen oder noch kompliziertere Strukturen aufzubauen.
Ich habe durch Probieren eine Ringwurst aus zwölf Oktaedern gefunden. Ein paar Symmetrieüberlegungen machen klar, dass die zwölf Oktaeder sich in der Tat exakt zum Ring schließen und nicht nur ungefähr (ein Unterschied, der beim Basteln in der üblichen Ungenauigkeit untergehen könnte). Der Ring besteht aus drei "unteren" Oktaedern, mit denen er flach auf dem Tisch liegt, drei "oberen", deren oberste Dreiecke ebenfalls in einer gemeinsamen horizontalen Ebene liegen, und sechs "mittleren", die jeweils ein oberes und ein unteres Oktaeder miteinander verbinden. Ein oberes Oktaeder geht durch eine simple Parallelverschiebung in das nächstgelegene untere Oktaeder über, denn gegenüberliegende Seitenflächen liegen beim Oktaeder allgemein (und bei den mittleren Oktaedern eben auch) genau parallel. Außerdem sind gegenüberliegende Seitenflächen entgegengesetzt orientiert: Wenn die vordere "Vorfahrt gewähren" sagt, sagt die hintere "Achtung" und umgekehrt. Beides zusammen ist dafür verantwortlich, dass obere und untere Oktaeder allgemein durch Parallelverschiebung auseinander hervorgehen. Dass obendrein die Vektoren dieser Parallelverschiebungen sich zu null addieren (und damit der Kreis sich schließt), das liegt an der Spiegelsymmetrie der beteiligten Oktaeder und der Symmetrie bezüglich Drehung mit 120 Grad um den Mittelpunkt eines obenliegenden Dreiecks.
Da der Ring so schön zwischen zwei parallele Ebenen passt (die wir uns bis jetzt beide horizontal vorgestellt haben), kann man diese beiden Ebenen auch als Spiegelebenen benutzen. Dadurch setzt man auf einen Ring einen weiteren auf, auf diesen noch einen und so beliebig weiter. Da die Ringe in sich "wellig" sind (sie gehen in einer Runde dreimal von oben nach unten und wieder zurück), ergibt sich aus dieser Stapelung von Ringen eine beliebig lange Röhre mit lauter rautenförmigen Löchern in den Wänden – ein sehr grobmaschiger Netzstrumpf.
Es geht noch etwas ganz anderes: Zwei obere Oktaeder, das untere zwischen ihnen und die beiden verbindenden mittleren Oktaeder können zusammen aufgefasst werden als ein Stück eines ganz anderen Rings. Der liegt schräg im Raum, und obere und untere Oktaeder haben ihre Rollen getauscht. Das Stück Ring kann man zu einem kompletten Ring ergänzen. Insgesamt bietet der Zwölferring drei solcher Möglichkeiten, einen weiteren Ring nach oben aus ihm herauswachsen zu lassen, und siehe da: Es entsteht ein merkwürdiges Kuppelgebilde aus vier Ringen. Von den insgesamt 22 Oktaedern gehören vier zu jeweils drei Ringen zugleich und die übrigen achtzehn immerhin zu je zwei Ringen.
Merkwürdigerweise hat die Kuppel als Ganzes wieder eine andere Symmetrie, nämlich die des Tetraeders. Die vier großen Löcher entsprechen den Flächen des Tetraeders, die roten Oktaeder, in denen sich jeweils drei Ringe treffen, den Ecken und die blauen Oktaeder den Kanten. "Symmetrie des Tetraeders" heißt: Jede Drehung oder Spiegelung, die das Tetraeder in sich selbst überführt, lässt auch die Oktaederkuppel unverändert. Jetzt geht das Spiel auf höherer Ebene weiter: So wie man auf jede Dreiecksfläche eines Tetraeders ein Dreierhütchen aufsetzen kann, so kann man diese Kuppel durch weitere Ringe erweitern. Wahrscheinlich sieht eine Zusammensetzung aus Tetraedern, die jedes durch eine Oktaederkuppel ersetzt sind, insgesamt ziemlich eindrucksvoll aus. Aber die mochte ich nicht mehr basteln.
Kommentare und Anregungen sind wie immer stets willkommen!
Herzlich Ihr
Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft
Schreiben Sie uns!
Beitrag schreiben