Räumliche Geometrie: Neue Körper entdecken - durch Entecken
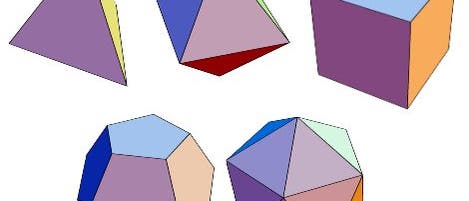
Platonische Käsewürfel
Zuweilen ist in der räumlichen Geometrie eine Betrachtungsweise von hohem Nährwert, die ich das Gouda-Prinzip nennen möchte: Man stelle sich vor, ein Polyeder bestehe aus einem homogenen, löcherfreien, schneidbaren, gelben und wohlschmeckenden Material. Das klassische Beispiel ist der Käsewürfel (kein Emmentaler!). Ferner stehe uns ein Messer zur Verfügung, mit dem man das Polyeder entlang einer beliebig gewählten Ebene zerteilen kann. Was kann man damit anstellen?
Zunächst: Aus jedem Polyeder wird durch Anwenden des Messers wieder ein Polyeder (plus ein zweites, das weggeschnittene; aber das essen wir auf, weil es nicht so interessant ist). Wenn das ursprüngliche Polyeder konvex war, dann gilt das auch für das beschnittene. Konvex heißt nämlich: Der Körper enthält mit je zwei Punkten auch deren Verbindungsstrecke; insbesondere gibt es keine einspringenden Ecken. Wenn man das etwas weiterdenkt, stellt man fest: Wenn ein konvexer Körper drei Punkte enthält, dann auch gleich das ganze Dreieck, dessen Ecken diese drei Punkte sind. Und wenn er vier Punkte enthält, die nicht alle in einer Ebene liegen, dann gehört auch das ganze Tetraeder, das von diesen vier Punkten aufgespannt wird, zum Körper.
Am Ende ergibt sich: Ein konvexes Polyeder ist genau dasselbe wie der (mengentheoretische) Durchschnitt endlich vieler Halbebenen. Oder, anschaulich ausgedrückt: Man beginne mit der Idealwelt der mathematisch vorgebildeten Hausmaus: ein ganzer unendlicher Raum voll Käse. Alles, was man mit endlich vielen ebenen (das heißt auch: unendlich ausgedehnten) Messerschnitten daraus schnitzen kann, heißt ein Polyeder. Manche Leute bestehen auch darauf, dass das Polyeder seinerseits endliches Volumen hat, schließen also unendlich lange Käsestangen aus der Betrachtung aus. Das ist soweit ja schön allgemein, aber im Allgemeinen nicht besonders ansehnlich. Wenn man die Schnittebenen irgendwie in den Raum legt, kommt auch nur ein irgendwie geformtes Stück Käse dabei heraus. Schöner wäre es, wenn von der Regelmäßigkeit eines platonischen Körpers wenigstens etwas übrig bliebe.
Das geht, und zwar zum Beispiel so: Man schneide einem platonischen Körper seine sämtlichen Ecken ab. Das nennt man "Ent-ecken". Wenn sich in einer Ecke beispielsweise drei Flächen getroffen haben, legt der Schnitt ein Dreieck frei. Der Regelmäßigkeit zuliebe führt man das Messer so, dass das Dreieck gleichseitig wird. Wie geht das? Nach einigem Überlegen erkennt man, dass die Schnittebene auf der Verbindungslinie von Eckpunkt und Mittelpunkt des Körpers senkrecht stehen muss. Es bleibt noch die Freiheit, mehr oder weniger viel – außer der Ecke selbst – von dem Körper wegzuschneiden.
Entecken konkret
Nutzen wir diese Freiheit, indem wir von den platonischen Körpern scheibchenweise die Ecken abschneiden (siehe die Kurzfilme im Bild links). So wie wir das Messer führen, sind die entstehenden Schnittflächen zunächst automatisch regelmäßige Vielecke – bis sie ihrerseits von anderen Schnittflächen kleiner gemacht werden. Was von den ursprünglichen Flächen übrigbleibt, ist von alleine nicht besonders regelmäßig. Aus den Fünfecken des Dodekaeders werden zunächst Zehnecke mit abwechselnd langen und kurzen Seiten; aber es gibt eine spezielle Schnitttiefe, für die alle Zehneckseiten gleich lang sind. Dann haben wir einen Körper aus zwölf gleichseitigen Zehnecken und zwanzig gleichseitigen Dreiecken – nicht gerade das Maximum an Ebenmaß, aber immerhin zweite Liga.
Der antike Philosoph Platon hatte es bekanntlich sehr mit dem Idealen und dem reinen Ebenmaß, weswegen er ein geeigneter Namensgeber für die platonischen Körper ist (auch wenn er mit deren mathematischer Herleitung nicht besonders befasst war). Archimedes, ein paar Jahrhunderte jünger, hatte es mehr mit der praktischen Anwendbarkeit und der Vielfalt. Deswegen passt auch die Bezeichnung "archimedische Körper" ganz gut. Archimedisch heißen diejenigen Polyeder, die wie die platonischen von regelmäßigen Vielecken begrenzt sind, aber nicht notwendig nur von einer Sorte. So sind zum Beispiel Dreiecke und Zehnecke in ein und demselben archimedischen Körper zugelassen.
Auf dem Wege nach innen macht das Käsemesser aus dem Dodekaeder noch einen Körper aus der zweiten Liga: den Bundesligafußball aus zwölf Fünfecken und zwanzig Sechsecken. Die dreieckigen Schnittflächen beschneiden sich nämlich inzwischen gegenseitig derart, dass von ihnen nur noch Sechsecke übrig bleiben.
Am Ende bleibt von den ganzen Dodekaeder-Käse – ein Ikosaeder, der zum Dodekaeder duale Körper. Mit etwas Nachdenken wird auch klar, warum: Dual ist, wenn man aus Ecken Flächen macht und umgekehrt. Entecken macht aus Ecken Flächen, und zwar so intensiv, dass von den ursprünglichen Flächen nur Ecken übrigbleiben. Verfolgen Sie das Schicksal der übrigen platonischen Körper! Das Ikosaeder wird zu seinem dualen Körper, dem Dodekaeder, und nicht nur das: Auch die Zwischenstationen Fußball und Zehnecks-Dreiecks-Körper sind dieselben. Es sieht ganz so aus, als sei der Film zum Ikosaeder die rückwärts laufende Version des Dodekaeder-Films.
Das gilt auch für das zweite Paar dualer platonischer Körper, nämlich Würfel und Oktaeder. Auf dem Weg vom einen zum anderen finden wir einen guten alten Bekannten wieder: den Oktaederstumpf aus Dreiecken und Sechsecken. Dazu kommt das so genannte Kuboktaeder aus Dreiecken und Quadraten (den Vorfahrtsschildern, die von den Quadraten des Würfel übrigbleiben, wenn jeder Schnitt jeweils eine halbe Kantenlänge wegnimmt). Das dritte Paar dualer Körper sind das Tetraeder und das Tetraeder. Bei der Verwandlung in die ziemlich klein geschnittene (und um 180 Grad gedrehte) Version seiner selbst liefert es auf halbem Wege eine Überraschung: Da steht plötzlich ein Oktaeder. Ein anderer archimedischer Körper taucht unterwegs sogar zweimal auf. Er besteht aus regelmäßigen Sechsecken und Dreiecken.
Entkanten
Suchen wir nach weiteren Möglichkeiten, mit dem Käsemesser platonische Körper möglichst ebenmäßig zu stutzen! Ein Gedanke liegt nahe: Man schneide statt Ecken ganze Kanten ab. Wieder soll der Schnitt schön symmetrisch liegen, insbesondere von beiden einer Kante benachbarten Flächen gleich viel abschneiden. Das läuft darauf hinaus, dass die Schnittebene senkrecht auf der Verbindungslinie von Mittelpunkt der Kante und Mittelpunkt des ganzen Körpers stehen muss. Damit ist sie automatisch auch parallel zur abgeschnittenen Kante.
Bei diesem Entkanten liefert abermals das Tetraeder eine Überraschung. Wenn man das Messer nur tief genug ansetzt, kommt ein Würfel heraus! Bei näherem Nachdenken legt sich die Überraschung ein bisschen: Ein Tetraeder hat sechs Kanten, also hat der stark entkantete Körper sechs Flächen, dann nämlich, wenn die Entkantung von den ursprünglichen Flächen des Körpers nichts mehr übrig lässt. Außerdem wahrt unsere Entkantungsmethode – symmetrisch wegschneiden und alle Kanten gleich behandeln – ein Maximum an Symmetrie. Was ist der symmetrischste Körper mit sechs Seitenflächen? Na bitte.
Das war leider ein bisschen schnell überlegt, und im Allgemeinen stimmt es auch nicht. Das sehen wir an den Entkantungen von Würfel und Oktaeder. Die haben nämlich beide jeweils zwölf Kanten, also ist der stark entkantete Körper zwölfflächig, der regelmäßigste Zwölfflächner, den es gibt, ist das Dodekaeder, und das – kommt nicht heraus. Pech gehabt.
Eine etwas weniger kurzsichtige Erklärung arbeitet mit Symmetrien. Dodekaeder und Ikosaeder haben fünfzählige Symmetrien. Das heißt, es gibt Drehachsen mit der Eigenschaft, dass eine Fünfteldrehung den Körper wieder in sich selbst überführt. Entsprechend haben Würfel und Oktaeder vierzählige Symmetrien. Alle platonischen Körper haben darüber hinaus noch drei- und zweizählige Symmetrien, aber daran kann man sie nicht unterscheiden. Dagegen haben Würfel und Oktaeder definitiv keine fünfzählige Symmetrie, und Dodekaeder und Ikosaeder keine vierzählige. Beim Entkanten und Entecken bleibt die Symmetrie des Körpers erhalten, also kann durch Entkanten und/oder Entecken ein Körper die Familie der Vierzähligen beziehungsweise Fünfzähligen nicht wechseln. Und deswegen wird aus einem vierzähligen Würfel oder Oktaeder niemals ein fünfzähliges Dodekaeder.
Und in welche Familie gehört das arme kleine Tetraeder? Na ja, irgendwie zum Würfel und zum Oktaeder, aber nicht richtig. Es hat nämlich von Natur aus keine vierzählige Symmetrie, aber immerhin die Anlage, eine solche Symmetrie auszubilden. Und diese Anlage kommt beim Entkanten und Entecken zum Tragen. Etwas weniger unwissenschaftlich ausgedrückt: Die Symmetriegruppe des Tetraeders ist eine Untergruppe der Symmetriegruppe des Würfels/Oktaeders. Was man zum Beispiel auch daran sieht, dass die acht Ecken eines Würfels sich in zwei Gruppen (die "roten" und die "blauen" Ecken) einteilen lassen, und die Ecken jeder Gruppe gehören zu einem Tetraeder (siehe Folge 2).
Und was ergibt sich nun beim Entkanten von Würfel und Oktaeder? Interessanterweise beidesmal derselbe Körper, und der ist ein guter alter Bekannter: das Rhombendodekaeder. Er spielte bei den Raumfüllungen von Arthur Schoenflies (siehe Folge 4) eine prominente Rolle, und sein Kollege, der Oktaederstumpf, kommt bei der Entkantung des Würfels auch vor. Irgendwie ist es klar: Das Endergebnis muss zwölfflächig sein, ziemlich regelmäßig, und zur Familie der Vierzähligen gehören. Da ist die Auswahl nicht so groß.
Was in der Fünfzähligen-Familie beim Entkanten passiert, kann man sich jetzt schon fast ausmalen. Sowohl Ikosaeder als auch Dodekaeder enden bei einem Körper aus dreißig Rauten, mit griechischem Namen Rhombentriakontaeder. Das Dodekaeder wird unterwegs noch zum Fußball. Dreißig gleiche, rautenförmige Flächen begrenzen diesen Körper. Aber die Ecken sind nicht alle gleich. In den "stumpfen" Ecken treffen sich jeweils drei Rauten mit ihren stumpfen Ecken, und in den "spitzen" Ecken treffen sich jeweils fünf Rauten mit ihren spitzen Ecken.
Diese beiden Rautenkörper sind nicht archimedisch, denn ihre Grenzflächen sind zwar alle gleich, aber nicht regelmäßige Vielecke. Ihre Duale sind allerdings archimedisch, und wir kennen sie schon vom Entecken: Es handelt sich um das Kuboktaeder und den Körper aus zwölf Fünfecken und zwanzig Dreiecken. (Der hat auch einen griechischen Namen: Ikosidodekaeder wie Zwanzig-zwölf-flächner. Aber irgendwie hat man keine Lust, sich den zu merken.)
Entecken und Entkanten zugleich
Irgendwie ist Entkanten nicht so ergiebig wie Entecken. Die Schnittflächen sind – jedenfalls zunächst – diese langgestreckten Sechsecke, die sich nicht immer zu regelmäßigen Sechsecken mausern. Wie ist es, wenn man ihnen die Enden auch noch abschneidet, sodass sie zu Rechtecken zurechtgestutzt werden und wieder gleichseitige Dreiecke erscheinen?
Das läuft auf Entkanten und Entecken zugleich hinaus, wobei die Schnitttiefen für Kanten und Ecken aufeinander abgestimmt sein müssen. Für große Schnitttiefen läuft das auf schieres Entecken und damit auf bereits Bekanntes hinaus. Aber unterwegs gibt es immerhin noch ein paar neue archimedische Körper zu bewundern, in denen Quadrate zahlreich und prominent vorkommen.
Den archimedischen Körper aus Dreiecken, Quadraten und Fünfecken haben Sie bestimmt schon einmal in der Vorweihnachtszeit gesehen, ohne es richtig zu merken: Er ist der innere Kern des Standard-Weihnachts-Straßendekorationssterns. Man setze auf jede Seitenfläche dieses Körpers eine ziemlich hohe, spitze Pyramide auf. Aber dieses Bauprinzip kommt erst in der nächsten Folge.
Kommentare und Anregungen sind wie immer stets willkommen!
Herzlich Ihr
Christoph Pöppe
Redakteur bei Spektrum der Wissenschaft
Schreiben Sie uns!
Beitrag schreiben