Mit einem supraleitenden Fußball lässt sich ein mathematisches Theorem überprüfen, das Topologie und Analysis miteinander verbindet. Darum drehte sich die zweite wissenschaftliche Veröffentlichung, an der ich beteiligt war. Nicht nur die Idee klingt verrückt; auch die Tatsache, dass ich an diesem Projekt beteiligt war, ist ungewöhnlich. Denn ich hatte während meines Physikstudiums nie mit Experimenten zu tun (es sei denn, der Studienplan zwang mich dazu). Sobald etwas eine Schraube hat, bin ich raus. Auch zur mathematischen Seite konnte ich nicht allzu viel beisteuern. Ich habe zwar auch mehrere Semester Mathematik studiert, aber nie in dem Bereich aktiv geforscht. Und was Fußball angeht, kann ich sowieso nicht mit Fachwissen brillieren.

Aber schon damals hat mich die Verbindung von abgefahrener Mathematik und handfest messbaren Phänomenen fasziniert. In diese Kategorie fällt das so genannte Atiyah-Singer-Index-Theorem. Auf den ersten Blick wirkt das Ergebnis enorm abstrakt und lebensfern; aber dessen Konsequenzen lassen sich in einem Fußball aus Messing in einem Labor nachweisen.

Auf das Forschungsthema bin ich durch Zufall aufmerksam geworden. Im Jahr 2014 hatte ich gerade meine Masterarbeit in einem anderen Themenbereich begonnen. Gegenüber meinem Arbeitsplatz befand sich das Gebäude der experimentellen Kernphysik, in dessen Keller sich ein Teilchenbeschleuniger befand sowie – für mich viel wichtiger – die Kaffeeküche inklusive Süßigkeiten. Dort verbrachte ich viel Zeit mit meinen Kommilitonen und hörte eines Tages ein Gespräch, bei dem jemand das Index-Theorem erwähnte. Ich war sofort neugierig.

Während meiner Bachelorarbeit (die nichts mit Fußbällen zu tun hatte) hatte ich von diesem mathematischen Satz gehört. Das Index-Theorem, so viel wusste ich noch, verbindet zwei Größen miteinander, die eigentlich nichts miteinander zu tun haben sollten. Die beiden Mathematiker Michael Atiyah und Isadore Singer bewiesen das Theorem im Jahr 1963 und begründeten damit ein ganzes mathematisches Gebiet: die Index-Theorie. Denn tatsächlich gibt es nicht nur das eine Index-Theorem; sie fanden eine ganze Reihe von ungeahnten Verbindungen. Dafür erhielten die beiden Forscher 2004 den renommierten Abelpreis, eine Art Nobelpreis der Mathematik.

»Als wir das Index-Theorem bewiesen, sahen wir, wie wichtig es für die Mathematik war, aber wir ahnten nicht, dass es einige Jahre später eine solche Wirkung auf die Physik haben würde«Isadore Singer, Mathematiker

»Ich ziehe es vor, es eine Theorie zu nennen, nicht ein Theorem. Wir haben 25 Jahre lang daran gearbeitet, und wenn ich alle damit zusammenhängenden Themen einbeziehe, habe ich wahrscheinlich 30 Jahre meines Lebens damit verbracht, mich mit diesem Gebiet zu beschäftigen. Es ist das Beste, was ich je gemacht habe«, sagte Atiyah in einem Interview mit Martin Raussen and Christian Skau. Und tatsächlich halfen die Brücken zwischen unterschiedlichen Bereichen der Mathematik dabei, die Barrieren zwischen den Fachgebieten einzureißen: »Als das Index-Theorem zum ersten Mal auftauchte, waren viele alteingesessene Fachleute verärgert darüber, dass neue Techniken in ihre Bereiche eindrangen. Eine jüngere Generation fühlte sich sofort von den Grenzen befreit, die wir beide als künstlich ansehen.«

Und tatsächlich rissen sie damit auch Mauern zur Physik ein. Denn das Index-Theorem mag recht abstrakt wirken, hat aber viele wichtige Konsequenzen. »Michael Atiyah verband Mathematik und Physik während der 1960er Jahre auf eine Weise, wie es sie seit Isaac Newton nicht mehr gab«, schrieb die »New York Times« in einem 2019 erschienenen Nachruf auf den Mathematiker. Dabei hatten die beiden Wissenschaftler nicht damit gerechnet. »Als wir das Index-Theorem bewiesen, sahen wir, wie wichtig es für die Mathematik war, aber wir ahnten nicht, dass es einige Jahre später eine solche Wirkung auf die Physik haben würde«, sagte Singer im Interview Raussen und Skau. Diese Verbindung zur Physik war der Grund, weswegen ich es während meines Studiums aufgeschnappt hatte.

Mathematik von Kaffeetassen und Donuts

Zu Beginn seiner Forscherkarriere beschäftigte sich Atiyah vor allem mit Topologie. Dieser Bereich ist eine Art sehr ungenaue Geometrie. In der Topologie geht es nicht darum, geometrische Objekte exakt zu vermessen. Ziel der Wissenschaft ist es, Gebilde ganz grob zu sortieren. Dazu stellt man sich vor, dass alle Objekte aus Knete bestehen. Kann man eine Figur in ein anderes verformen, ohne dabei ein Loch hineinzureißen oder verschiedene Teile zusammenzukleben, gelten die Figuren als gleich. Entsprechend sind für Topologen Tassen und Donuts gleich – denn beide Objekte haben exakt ein Loch und lassen sich daher ineinander umformen.

1955 traf Atiyah auf Isadore Singer, der an Differenzialgleichungen forschte. Das sind Gleichungen, die Ableitungen enthalten und insbesondere in der Physik eine wichtige Rolle spielen. Denn alles, was veränderlich ist, wird durch eine Differenzialgleichung charakterisiert, ob ein fahrendes Auto, die Strömung eines Flusses oder die Elektronen innerhalb eines Materials. »Manche Teile der Mathematik wurden geschaffen, um die Welt um uns herum zu beschreiben«, sagte Singer im Interview mit Raussen und Skau. »Analysis, Differenzialgleichungen und Integrale sind ein natürlicher Bestandteil der Physik, da sie für die Physik entwickelt wurden.« Das Problem ist: In den seltensten Fällen lassen sich Differenzialgleichungen exakt lösen. Okay, die Geschwindigkeit eines fahrenden Autos kann man berechnen, aber bei Flüssen sind Fachleute aufgeschmissen. Die so genannten Navier-Stokes-Gleichungen, die sie beschreiben, sind zwar bekannt, aber niemand kann sie lösen – es ist nicht einmal klar, ob überhaupt eine Lösung existiert.

Singer kannte die Arbeiten von Atiyah und hoffte, dass sie gemeinsam mit topologischen Methoden die Differenzialgleichungen knacken könnten. »Es war aufregend, all diese Jahre mit Sir Michael zu arbeiten. Und es ist heute noch genau so wie damals, als wir uns zum ersten Mal trafen – dieses Gefühl der Aufregung und des ›alles ist möglich‹«, sagte Singer 2004. Doch eines war nicht möglich: exakte Lösungen zu finden. Dafür stießen sie auf einen Zusammenhang zwischen ihren Gebieten, mit dem keiner gerechnet hatte.

Das Index-Theorem für Graphen

Wenn man eine Differenzialgleichung auf einer Oberfläche betrachtet (etwa für einen Ball, der auf einer Kugel rollt), dann bestimmt die Topologie der Oberfläche – insbesondere die Anzahl der Löcher –, wie viele Lösungen die Differenzialgleichungen besitzt. Mathematiker sagen: Der analytische und der topologische Index sind gleich.

Das klingt jetzt zunächst nicht sonderlich spektakulär. Was bringt es, zu wissen, wie viele Lösungen es gibt, wenn man die Lösung selbst nicht kennt? In der Physik ist das tatsächlich ungeheuer nützlich. Zum Beispiel für Graphen, dem ersten zweidimensionalen Material der Geschichte.

Graphen besteht aus Kohlenstoffatomen, die in einem hexagonalen Gitter angeordnet sind – etwa wie die Honigwaben von Bienen. Dabei handelt es sich um eine einatomige Schicht von eigentlich dreidimensionalem Graphit. Graphen lässt sich beispielsweise herstellen, indem man eine Bleistiftmine mit Klebeband abzieht (kein Witz, dafür gab es einen Physik-Nobelpreis). Der Grund, warum Physiker durch die Entdeckung von Graphen so aus dem Häuschen waren, sind die besonderen elektronischen Eigenschaften des Stoffs. Einige der Elektronen benehmen sich darin völlig anders als in normalen Festkörpern. Die Differenzialgleichung, die ihre Bewegung beschreibt, ähnelt der von Lichtteilchen (auch wenn sich die Elektronen natürlich nicht mit Lichtgeschwindigkeit durch Graphen bewegen).

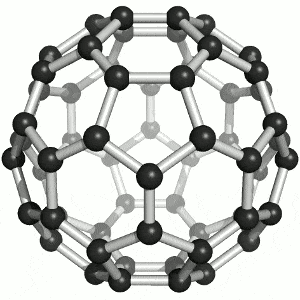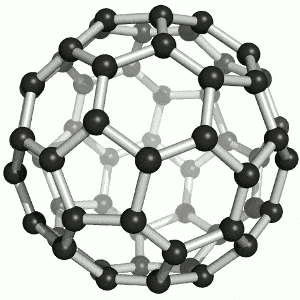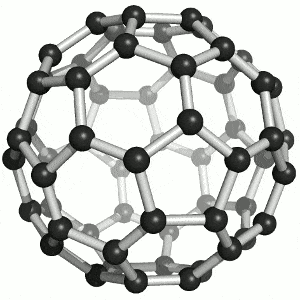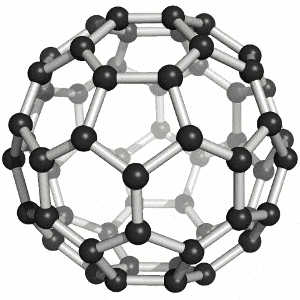
Physikerinnen und Physiker möchten wissen, wie viele von diesen seltsamen lichtartigen Elektronen in Graphen vorhanden sind, weil sie über die Strom leitenden Eigenschaften des Stoffs bestimmen. Und genau hierbei kann das Index-Theorem helfen. Denn je nachdem, welche Form der Festkörper hat, variiert die Anzahl der Lösungen der Differenzialgleichungen – und damit der lichtartigen Elektronen. Stoffe wie Graphen existieren nicht nur als ebene Fläche, sondern es gibt auch Fullerene: Kugeln aus Graphen, die aussehen wie ein Fußball. An jeder Ecke der Sechs- und Fünfecke befinden sich dabei die Kohlenstoffatome.

Und genau diese Vorhersage des Index-Theorems wollte die Arbeitsgruppe, die ich im Keller des Kernphysikgebäudes traf, testen. Allerdings nicht direkt mit Fullerenen – die elektronischen Zustände in einem winzigen Molekül zu messen, ist schwierig – sondern mit einem supraleitenden Fußball. Dieser bestand aus supraleitenden Wellenleitern und runden Hohlraumresonatoren, in welche die Physiker Mikrowellenstrahlen schickten. Diese breiten sich entlang des Fußballs so aus, wie es die Elektronen in Fullerenen tun. Damit ließ sich prüfen, ob das Index-Theorem Recht behält.

»Wir liefern die erste experimentelle Realisierung von ›künstlichem‹ Fulleren und die Verifizierung des Atiyah-Singer-Index-Theorems in einem makroskopischen System«Barbara Dietz, Physikerin

Für ein solches kugelförmiges Fulleren sagt das Index-Theorem sechs lichtartige Teilchen voraus – und genau sechs dieser Mikrowellen-Signale konnte die Arbeitsgruppe messen. »Wir liefern damit die erste experimentelle Realisierung von ›künstlichem‹ Fulleren und die Verifizierung des Atiyah-Singer-Index-Theorems in einem makroskopischen System«, lässt sich in der Veröffentlichung nachlesen.

Das war eines der spannendsten Projekte, an denen ich mitgewirkt habe. Trotzdem wundere ich mich ehrlich gesagt noch heute, dass ich auf der Veröffentlichung als Koautorin auftauche. Denn an dem Experiment habe ich nicht mitgearbeitet; ich war eher beratend tätig und habe versucht, die abstrakte Mathematik hinter dem Versuch zu vermitteln – so wie jetzt auch. Manche Dinge ändern sich glücklicherweise nicht.