Ich habe nachgezählt: In meinem Leben bin ich bisher 14-mal umgezogen. Als Hobby kann ich das niemandem empfehlen; aber es hält fit und man lernt, die Größe des Haushalts auf ein Minimum zu reduzieren. Dank der vielen Wohnungswechsel habe ich außerdem eine ganz besondere Verbindung zu einem mathematischen Problem, dem so genannten Sofaproblem: Wie sieht das größtmögliche Sofa aus, das sich entlang eines Gangs um eine Ecke schieben lässt? Obwohl die Frage schon 1966 aufgeworfen wurde und sich seither einige Fachleute damit beschäftigt haben, wurde es erst im November 2024 von einem jungen Mathematiker in seiner Doktorarbeit gelöst.

Man braucht nicht viel Fantasie, um sich vorzustellen, wie der Geometer Leo Moser vor rund 60 Jahren auf das Sofaproblem kam – vor allem, wenn man bedenkt, dass man für eine Karriere in der Wissenschaft meist häufig den Wohnort wechseln muss. Anders als so manch andere Mathematiker hatte Moser großen Spaß an alltäglichen Herausforderungen. Er sammelte sie in einem Buch und bat seine Gäste, Freunde und Kollegen, ähnliche Fragen und Rätsel darin einzutragen.

Das Sofaproblem zählt zur Kategorie der zweidimensionalen Geometrierätsel. Das Sofa, das um eine rechtwinklige Ecke bewegt werden soll, ist so schwer, dass es sich nicht anheben lässt. Daher schiebt man es – entlang eines schlauchförmigen Gangs, der um 90 Grad abknickt. Mosers Frage lautete: Was ist das flächenmäßig größte Sofa, das man derart um die Ecke befördert bekommt?

»Diese geometrischen Optimierungsprobleme können höllisch schwer sein«, schrieb der mathematische Physiker John Baez auf dem sozialen Netzwerk »Mastodon«. Denn das Sofa kann unendlich viele verschiedene Formen annehmen. Es ist zwar einfach, Beispiele für Sofas zu finden, die um die Ecke passen. Aber zu beweisen, dass es sich dabei um die bestmögliche Lösung handelt, ist extrem kompliziert.

Mögliche Formen eines Sofas

Angenommen, der Gang ist einen Meter breit. In diesem Fall könnte das Sofa eine quadratische Fläche von 1 haben (ich lasse im Folgenden die Einheiten weg) und würde um die Ecke passen. Doch es gibt bessere Lösungen: zum Beispiel ein halbkreisförmiges Sofa mit einem Radius von 1. Dieses hätte eine Fläche von ^π⁄₂ ≈ 1,57 – also mehr als 50 Prozent größer als die quadratische Lösung.

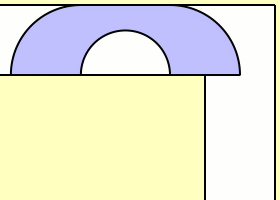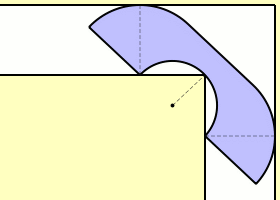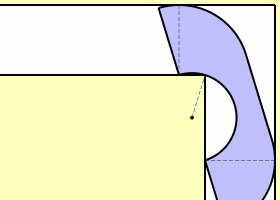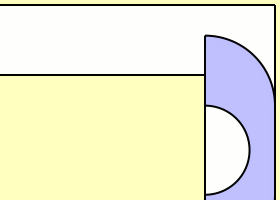
1968 fand der Mathematiker John Hammersley aber eine noch bessere Lösung. Er erkannte, dass größere Sofas um die Ecke passen, wenn sie die Form eines Telefonhörers annehmen. Den zuvor betrachteten Halbkreis kann man dazu in zwei Hälften teilen und anschließend durch ein Verbindungsstück zusammenfügen, aus dem ein halbkreisförmiges Segment herausgeschnitten wurde.

Die zusätzliche Fläche des Verbindungsstücks erweitert also die Größe des Sofas. Hammersley legte sich auf folgende Form fest: zwei Viertelkreise, die durch ein gerades Verbindungsstück zusammenhängen, aus dem ein Halbkreis ausgespart ist. Davon ausgehend bestimmte er, was das größtmögliche Verbindungsstück ist, das es erlaubt, ein solches Sofa um die Ecke zu transportieren. Seinen Berechnungen zufolge muss es eine Länge von ⁴⁄_π haben, so dass ein Halbkreis mit Radius ²⁄_π herausgeschnitten ist. Die gesamte Fläche des telefonhörerförmigen Sofas beträgt damit ^π⁄₂ + ²⁄_π ≈ 2,2074.

In den nächsten 24 Jahren gab es keine Fortschritte auf dem Gebiet. Die Lösung von Hammersley überzeugte viele Fachleute davon, dass die Form eines Telefonhörers wahrscheinlich die vielversprechendste ist. Aber niemand konnte beweisen, dass die miteinander verbundenen Viertelkreise wirklich die größtmögliche Fläche ergeben.

Kleine Änderungen mit großer Wirkung

Im Jahr 1992 nahm sich der Mathematiker Joseph Gerver des Sofaproblems an und fand eine bessere – aber auch deutlich kompliziertere – Lösung.

Die Form des von ihm konstruierten Sofas erinnert stark an jene von Hammersley, aber sie ist deutlich ausgeklügelter. Sie besteht aus drei geraden Linien und 15 Kurven, die zusammengesetzt ebenfalls einem Telefonhörer ähneln. Gerver rundete unter anderem die Ecken der äußeren Viertelkreise ab und wandelte die kreisförmigen Segmente leicht ab. Auch wenn die vorgenommenen Änderungen auf den ersten Blick willkürlich erscheinen, folgte Gerver dabei strengen mathematischen Überlegungen.

Das Gerver-Sofa hat eine Fläche von etwa 2,2195 und ist damit größer als die Lösung von Hammersley. In seiner Arbeit konnte Gerver zudem beweisen, dass das Sofa zumindest lokal die beste Lösung darstellt. Das heißt: Wenn man die Form nur leicht verändert, wird man keine größere Fläche konstruieren können, die um die Ecke passt.

Das sahen viele Mathematiker als Hinweis dafür, dass das Gerver-Sofa tatsächlich die optimale Variante sein könnte. Doch ein vollständiger Beweis ist das nicht. Es könnte noch immer eine stark veränderte Form mit größerer Fläche geben, die sich um die Ecke schieben lässt.

In den kommenden Jahren bissen sich weitere Fachleute die Zähne an dem Problem aus. Doch niemand konnte belegen, ob Gervers Sofa nun das größtmögliche ist oder nicht. Der Mathematiker Dan Romik von der University of California in Davis versuchte zum Beispiel, die maximale Größe des Sofas durch Abschätzungen einzugrenzen. Im Jahr 2018 bewies er, dass die Fläche eines Sofas zwingend kleiner als 2,37 sein muss. Seine Hoffnung bestand darin, den Wert weiter zu senken, um schließlich bei 2,2195 zu landen – damit wäre beweisen, dass Gervers Sofa die optimale Lösung des Problems ist. Doch das gelang ihm nicht.

Frischer Wind

Während seiner Doktorarbeit stieß der junge Mathematiker Jineon Baek, der inzwischen an der koreanischen Yonsei University als Postdoc arbeitet, auf das Sofaproblem. Er dachte zwei Jahre lang intensiv darüber nach und arbeitete einen Plan aus, um die Frage anzugehen. Fünf weitere Jahre brauchte er dann für die Ausarbeitung aller Details. »Ich habe sehr viel Zeit in diese Arbeit investiert, ohne dass sie bisher veröffentlicht wurde«, sagte Baek zu »New Scientist«. »Die Tatsache, jetzt der Welt verkünden zu können, dass ich etwas Wertvolles zu diesem Problem beigetragen habe, empfinde ich als Bestätigung.«

Baek untersuchte zunächst eine kleine Auswahl an möglichen Sofaformen. Mit diesen konnte er ableiten, welche Eigenschaften ein Sofa erfüllen muss, um als optimale Lösung in Frage zu kommen. Zum Beispiel müssen die Umrisse des Sofas stets glatt sein und sollten keine Ecken enthalten. Anstatt sich dann auf den Flächeninhalt der Form zu konzentrieren, führte Baek eine neue Größe namens »Q« ein, die sich besser untersuchen lässt. Auf insgesamt 119 Seiten konnte er damit zeigen, dass das Gerver-Sofa tatsächlich die optimale Lösung darstellt.

»Ich weiß, dass ich das niemals hätte tun können«Dan Romik, Mathematiker

Während seiner Arbeit tauschte sich Baek immer wieder mit Romik aus, dem führenden Experten auf dem Gebiet. Dieser stellte fest: »Ich weiß, dass ich das niemals hätte tun können.« Baek sei aus einer ganz anderen Richtung an die Sache herangegangen.

Damit hat das Sofaproblem nach fast 70 Jahren endlich eine Lösung. Vor einem Umzug lässt sich nun also prüfen, welche Couch mathematisch gesehen am besten in die neue Wohnung passt. Ich hatte bei meinen Umzügen zum Glück niemals ein so schweres Sofa, das es sich nicht anheben ließ – notfalls konnte ich (zusammen mit meinen Umzugshelfern natürlich) also immer auf die dritte Raumdimension ausweichen. Die Schwierigkeiten, auf die ich viel öfter stieß, hatten mit engen Treppenhäusern und hohen Bücher- oder Kleiderschränken zu tun. Wer weiß, vielleicht widmen sich Geometer ja bald dem dreidimensionalen Kleiderschrankproblem?