Sehr viel eindeutiger kann ein Wahlergebnis nicht ausfallen: In 98 von 99 Bezirken des US-amerikanischen Gliedstaats Iowa hat sich Donald Trump gegen die internen Herausforderinnen und Herausforderer der Republikanischen Partei durchgesetzt. Doch etwas sticht bei genauerem Hinsehen heraus. In dem einen Bezirk, den Trump nicht holen konnte, gewann die Politikerin Nikki Haley mit nur einer Stimme Vorsprung. In Johnson County stimmten 1271 Personen für Haley und 1270 für Trump. Schnell wurden Stimmen in den sozialen Medien laut, man solle den Bezirk noch einmal neu auszählen. Ein so knapper Wahlsieg schien vielen verdächtig.

Das Ergebnis stach auch dem pensionierten Physiker Franz Pichler aus Wien ins Auge – und er beschloss, den Ausgang mit statistischen Methoden genauer unter die Lupe zu nehmen: Wie wahrscheinlich ist es, in einem Bezirk mit 2541 Wahlgängern einen Sieg mit nur einer Stimme Differenz davonzutragen? Wie Pichler herausfand, liefert die Mathematik eine deutliche Antwort darauf.

Um solche Fragen mathematisch anzugehen, bieten sich statistische Simulationen an: Man modelliert die Wahlsituation immer und immer wieder und wertet aus, wie häufig der zu untersuchende Ausgang eintritt. Ignoriert man die Stimmen, die an die übrigen republikanischen Kandidaten wie Ron DeSantis in der Vorwahl gingen, haben etwa 50 Prozent der Wahlgänger in Johnson County Donald Trump und die übrigen 50 Prozent Nikki Haley gewählt. Deshalb ordnete Pichler in seiner Simulation die betreffenden 2541 Stimmen mit einer Wahrscheinlichkeit von ½ dem einen oder dem anderen republikanischen Kandidaten zu.

Eine simulierte Wahl durch Münzwürfe

Auf diese Weise simulierte Pichler eine Situation, bei der jeder der 2541 Wahlgänger in der Wahlkabine eine Münze wirft, und das Kreuz dann entsprechend für Trump (etwa bei Kopf) oder Haley (bei Zahl) setzt. Dann wertete der Physiker aus, welche Stimmendifferenz sich am Ende des Urnengangs ergibt. Um daraus eine Aussage abzuleiten, wiederholte er die simulierte Wahl – und zwar 30 000-mal.

Natürlich saß Pichler nicht mit einer Münze am Schreibtisch, die er für jeden der 2541 Wähler 30 000-mal warf (was knapp 76,2 Millionen Münzwürfen entsprechen würde). Stattdessen verwendete er das Computeralgebrasystem »Mathematica« von Wolfram Research. Mit diesem lassen sich solche Berechnungen durch wenige Klicks durchführen. Als sich Pichler die Stimmendifferenzen der 30 000 durchgeführten Simulationen grafisch darstellen ließ, erkannte er, dass die Ergebnisse einer Normalverteilung folgen, die etwa um die Zahl 0 herum zentriert scheint.

Das war keine große Überraschung, schließlich folgen die Ausgänge von Münzwürfen einer Binomialverteilung. Und gemäß des Satzes von Moivre-Laplace nähert sich die Binomialverteilung für große N (in unserem Fall die Anzahl der Simulationen) einer Normalverteilung.

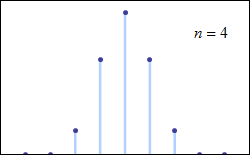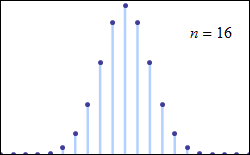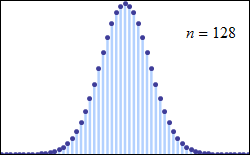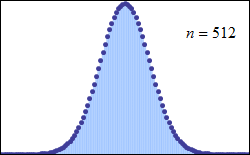
Das Ergebnis verdeutlicht, dass die Wahlergebnisse zwischen zwei Kandidaten häufiger nah beieinanderliegen, als dass sie voneinander abweichen – zumindest in dem simulierten mathematischen Modell, bei dem beide Kandidaten gleich beliebt sind. Aber wie wahrscheinlich ist es, dass sich die Ergebnisse bloß um eine Stimme unterscheiden? Oder anders ausgedrückt: Wie viele Wahlen dieser Art sind nötig, damit ein so knappes Wahlergebnis eintritt?

Wie oft müsste die Wahl für ein solches Ergebnis wiederholt werden?

Um das zu untersuchen, griff Pichler wieder auf Mathematica zurück. Auch dieses Mal ließ er das Programm die 2541 Münzwürfe nacheinander durchführen, doch nun sollte die Software stoppen, sobald sich am Ende eines simulierten Urnengangs eine Stimmendifferenz von 1 ergab. Pichler ließ den Algorithmus dann verzeichnen, wie viele Simulationen nötig gewesen waren, um diesen Wahlausgang zu erhalten. Und dann startete er den Vorgang wieder von Neuem. Diesmal ließ der Physiker die Berechnungen 10 000-mal wiederholen, um eine verlässliche statistische Aussage zu erhalten.

Das Programm stellte die Anzahl der Wahlsimulationen, die nötig sind, damit eine Stimmendifferenz von 1 eintritt, grafisch dar. Wie sich erkennen lässt, folgen die Ergebnisse einer Exponentialverteilung: Oft sind nur wenige Wiederholungen nötig, bis sich das Endergebnis der simulierten Wahl um nur eine Stimme unterscheidet. Dass ein solches Wahlresultat erst nach vielen Wiederholungen eintritt, kam in den Simulationen nur sehr selten vor.

Um eine quantitative Aussage treffen zu können, wollte Pichler den Median der erhaltenen Datenpunkte bestimmen. Der Median markiert jenen Punkt, der die gesamte Datenmenge in zwei gleich große Teile teilt: 50 Prozent der Datenpunkte befinden sich dann links des Medians und die restlichen 50 rechts davon. Damit liefert der Median einen Mittelwert, der nicht zu stark von statistischen Ausreißern abhängt: Wie viele Wahlwiederholungen sind im Schnitt (gemessen an dem Median) nötig, um ein Ergebnis wie in Johnson County hervorzubringen?

Eine Möglichkeit, den Median zu bestimmen, besteht natürlich darin, die simulierten Datenpunkte zu durchwühlen und sie zu zählen. Ein genaueres Ergebnis lässt sich jedoch erzielen, wenn man die zu Grunde liegende Exponentialverteilung untersucht. Denn diese gibt den Verlauf im Grenzfall unendlich oft wiederholter Simulationen an. Die Exponentialfunktion λe^-λx enthält dabei den Parameter λ, der von der Anzahl der abgegebenen Stimmen abhängt: ¹⁄_λ = √(2π·2541). Der Median einer Exponentialverteilung ist durch diesen Parameter festgelegt, nämlich: ^ln(2)⁄_λ.

Um den richtigen Wert für den Median zu berechnen, muss man allerdings noch ein paar Kleinigkeiten beachten. In der kontinuierlichen Exponentialverteilung könnte jede beliebige Stimmendifferenz auftauchen. In dem betrachteten Beispiel der Wahl in Johnson County sind aber nur 2541 Stimmen abgegeben worden, daher ist nur eine ungerade Differenz zwischen beiden Kandidaten möglich. Deshalb muss man das Ergebnis des Medians halbieren. Ein weiterer Faktor ½ taucht auf, weil es zwei mögliche 1-Stimmen-Differenzen gibt: entweder plus oder minus eins. Damit ergibt sich für den Median folgende Rechnung: ^ln(2)⁄₄·√(2π·2541) ≈ 21,90.

»​​Dieses Ergebnis hat mich sehr überrascht, ich hatte einen viel höheren Wert erwartet«Franz Pichler, Physiker

Das bedeutet: Im Schnitt müsste man eine Wahl wie in Johnson County 22-mal wiederholen, damit sich das Wahlergebnis mindestens einmal um nur eine Stimme zwischen zwei Kandidaten unterscheidet. Oder: Falls ein Staat aus mehreren Bezirken besteht, in denen zwei Kandidaten ungefähr gleich beliebt sind (was in manchen Counties von Iowa der Fall zu sein scheint) und jeweils die gleiche Anzahl an Stimmen abgegeben werden, dann tritt so ein knapper Wahlausgang durchschnittlich einmal pro 22 Wahlbezirken ein. »Dieses Ergebnis hat mich sehr überrascht, denn ich hatte einen viel höheren Wert erwartet«, sagt Pichler.

Besonders unwahrscheinlich ist der knappe Sieg von Nikki Haley in Johnson County also nicht – im Gegenteil. Ob diese statistische Argumentation die skeptischen Trump-Anhänger überzeugen wird, bleibt allerdings fraglich.