Das Christoffel-Symbol heißt auch Levi-Civita-Zusammenhang (engl. Levi-Civita connection) oder affiner/metrischer Zusammenhang. Es ist eine mathematische Größe in der Differentialgeometrie und insbesondere in der Allgemeinen Relativitätstheorie (ART). Das Christoffel-Symbol eignet sich, um die Krümmung einer Raumzeit ausrechnen zu können.

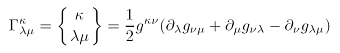
Berechnung

Der Levi-Civita-Zusammenhang ist im Prinzip eine Summe von partiellen Ableitungen der Metrik, wie die Definitionsgleichung oben zeigt. Die Gleichheit der Klassen von affinen und metrischen Geodäten einer pseudo-Riemannschen Mannigfaltigkeit erfordert zwingend das Verschwinden der kovarianten Ableitung des metrischen Tensors (siehe auch Linienelement). Dann ist der metrische Zusammenhang notwendigerweise symmetrisch, d.h. für die Gleichung oben, dass Vertauschen der Indizes λ und μ bei Γ den Levi-Civita-Zusammenhang nicht verändern.

Christoffel-Symbole in der Praxis

Die Berechnung der Christoffel-Symbole ist erforderlich, wenn man die Einsteinschen Feldgleichungen einer beliebigen Metrik, wie z.B. die Schwarzschild-Lösung oder die Kerr-Lösung in der ART formulieren möchte. Man kann sagen, dass die Christoffel-Symbole der ART die Rolle der Newtonschen Gravitationskraft übernehmen. Die Christoffel-Symbole enthalten erste Ableitungen der Metrik. Der Riemannschen Krümmungstensor berechnet sich wiederum aus ersten Ableitungen der Christoffel-Symbole, d.h. er enthält zweite Ableitungen der Metrik. Aus dem Riemann-Tensor berechnet man durch Verjüngung schließlich den Einstein-Tensor und folgert so die Feldgleichungen – nun spezifiziert auf eine bestimmte Metrik. Die Krümmungseigenschaften und die Dynamik der Raumzeit stecken in dieser fundamentalen Gleichung der Einsteinschen Gravitation.

Torsionsfreiheit

Die Symmetrie der Christoffel-Symbole hat weitere Konsequenzen, wie man an der Definition des Torsionstensors (in dem Eintrag dort) betrachtet. Der Torsionstensor ist ein Tensor vom Typ (1,2), der aus einer Differenz von Christoffel-Symbolen – die selbst keine Tensoren sind! – gebildet wird. Bei einem symmetrischen Zusammenhang verschwindet dieser Torsionstensor. Mit anderen Worten: Einsteins ART ist eine torsionsfreie Gravitation!

Gravitation mit Torsion

Die Torsionsfreiheit wird in manchen alternativen Gravitationstheorien aufgegeben. Einstein hat 1928 selbst in der Theorie vom Fernparallelismus einen solchen Ansatz gewählt, um Gravitation und Elektromagnetismus in einer neuen Feldtheorie zu vereinheitlichen. Er scheiterte zwar, aber in der modernen Gravitationsforschung werden weiterhin solche Gravitationstheorien mit Torsion unter der Bezeichnung fernparallele Gravitation (engl. teleparallel gravity) erforscht. Eine Übersicht der Themen in der aktuellen Gravitationsforschung wird im Lexikoneintrag Gravitation vorgestellt.