Es handelt sich um ein geeignetes Koordinatensystem, dass die Koordinatensingularität nicht rotierender Schwarzer Löcher beseitigt.

Das Problem

Das Linienelement der Schwarzschild-Lösung, die statische Schwarze Löcher beschreibt, hat in seiner historisch ursprünglichen Form ('Schwarzschild-Koordinaten') eine Unzulänglichkeit: Nur für eine unendliche Koordinatenzeit würde dort der Ereignishorizont erreicht werden. Diese Schwarzschildsche Koordinatenzeit wäre daher nur für einen weit entfernten Beobachter sinnvoll, da dies seiner Eigenzeit entsprechen würde. Tatsächlich erreicht ein radial einfallender Testkörper aber in endlicherZeit den Horizont, weshalb sich eine Koordinatentransformation zum Studium dieses Problems anbietet.

Die Lösung: eine Koordinatentransformation

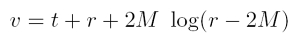Sir Arthur Eddington (1924) und später David Finkelstein (1958) haben nun die später nach ihnen benannten Eddington-Finkelstein-Koordinaten eingeführt. Die Transformationsvorschrift ist gerade in der Gleichung rechts dargestellt: die neue Zeitkoordinate v enthält die alte Zeitkoordinate t, hängt aber auch von der Radialkoordinate r ab (M ist die Lochmasse).
In dieser neuen Koordinatenzeit werden die einfallenden radialen Nullgeodäten zu Geraden. Dies liefert dann die Eddington-Finkelstein-Form der Schwarzschild-Lösung, die mathematisch die analytische Erweiterung der klassischen Schwarzschild-Lösung ist. Die Lösung in Eddington-Finkelstein-Koordinaten ist allerdings nicht mehr zeitsymmetrisch! Eine zeitumgekehrte Lösung findet man durch Einführen einer weiteren Zeitkoordinate, was radial auslaufende Geodäten zu Geraden macht. In diesem Sinne unterscheidet man die Schwarzschild-Lösung in avancierten und retardierten Eddington-Finkelstein-Koordinaten. Die folgende Gleichung stellt das Linienelement der Schwarzschild-Lösung in der avancierten Eddington-Finkelstein-Form dar. Wie man sieht, handelt man sich durch die Transformation einen Kreuzterm zwischen Zeit- und Radialkoordinate ein. Der metrische Tensor besitzt also zwei Nebendiagonalelemente.

Trennung durch Horizont

Man kann zeigen, dass die Fläche bei r = 2M (Schwarzschildradius, in geometrisierten Einheiten), die Funktion einer semipermeablen Membran zukommt, die für die avancierte Lösung nach innen und für die retardierte Lösung nach außen für Teilchen durchlässig ist! Aus diesem Grund heißt diese Fläche Ereignishorizont, da sie die Grenze aller Ereignisse darstellt, die außen noch beobachtbar sind. Die 'inneren Ereignisse' innerhalb r = 2M bleiben also jedem äußeren Beobachter verborgen.