Dieser englische Fachbegriff wird in dieser Form auch im deutschsprachigen Fachjargon verwendet, weil er sich schlecht ins Deutsche übersetzen lässt. Es handelt sich um einen rein allgemein relativistischen Effekt, der mit der Allgemeinen Relativitätstheorie (ART) beschrieben wird und nicht in der Newtonschen Physik existiert. Frame-Dragging besagt, dass jede rotierende Masse das lokale Bezugssystem (engl. reference frame) mitzieht (engl. 'ziehen': to drag). Anders gesagt wird alles von der rotierenden Masse gezwungen sich mit der Drehrichtung der Masse zu drehen. Das gilt für andere Testmassen, für Licht (Lichtkegel, Photonen), für lokale Beobachter – denn die Raumzeit von rotierenden Massen rotiert selbst.

rotierende Massen in Einsteins Gravitation

Rotierende Raumzeiten besitzt zwei Symmetrien: Achsensymmetrie (Axialsymmetrie) und Stationarität. Das entsprechende Linienelement kann ganz allgemein notiert werden (Papapetrou-Form). Es gibt da einige Spezialfälle: Ist die rotierende Masse ein Massenmonopol, so resultiert die Kerr-Lösung. Demgegenüber weisen Neutronensterne, die ebenfalls rotieren, einen Massenquadrupol auf. Doch beide Metriken sind axialsymmetrisch und stationär.
Der Frame-Drag tritt immer bei rotierenden Massen auf! In der Regel ist er allerdings verschwindend gering und schwierig zu messen – wie im Falle der rotierenden Erde. Das liegt daran, weil die Erde kein kompaktes Objekt ist. Die Effekte werden erst bei schnell rotierenden Neutronensternen (siehe auch Pulsar) und rotierenden Schwarzen Löchern besonders stark. Je mehr Masse auf kleinem Raum rotiert, umso heftiger ist Frame-Dragging.

Historisches & Aktuelles

Frame-Dragging wurde bereits 1918 von den beiden österreichischen Physikern Joseph Lense (1890 – 1985) und Hans Thirring (1888 – 1976) entdeckt. Deshalb nennt man ihn auch Lense-Thirring-Effekt. Unter diesem Lexikoneintrag wird die Mathematik des Frame-Draggings sowie deren Messung mit dem Satelliten Gravity Probe-B beschrieben.

Schleudertrauma am Kerr-Loch

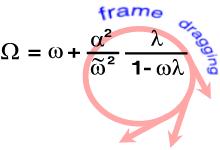Das Frame-Dragging der Kerr-Löcher ist mathematisch anhand der Gleichung (notiert in Boyer-Lindquist-Koordinaten) rechts zu verstehen: Winkelgeschwindigkeit des Loches ω, Lapse-Funktion α, Winkelgeschwindigkeit Ω und Zylinderradius (ω mit Schlange) sind Funktionen, die die rotierende Metrik bestimmen; λ ist der spezifische Drehimpuls des Teilchens, das um das Loch rotiert. Am Ereignishorizont verschwindet α (Definition des Horizonts!), so dass in jedem Fall der zweite Term null ist. Die Rotation des Teilchens, genauer die Winkelfrequenz Ω, wird nun vollständig bestimmt von der Winkelfrequenz des Schwarzen Loches ω, der so genannten Frame-Dragging-Frequenz: Das rotierende Loch reißt alles mit sich! Dabei ist es völlig unerheblich, welchen Drehimpuls (welches λ) das einfallende Teilchen hat.

Messen des rotierenden Raums

Auch wenn der Effekt klein ist, haben dennoch Physiker versucht, den Frame-Dragging-Effekt bei der Erde zu messen. Dies geschah mithilfe der LAGEOS-Satelliten, deren Position und Bewegung mittels Laser sehr genau bekannt ist. 1997 fanden sie noch eine schwache Evidenz mit hohem Messfehler (zwischen 25 und 200%); 2004 hat die gleiche Forschergruppe mehr Erfolg gehabt und mit hoher Wahrscheinlichkeit – sogar vor der dafür konzipierten Satellitenmission Gravity Probe-B – den Frame-Drag der Erde nachgewiesen (Ciufolini et al., Nature 431, 958, 2004).
Als Testmasse benutzen die Physiker Gyroskope, im Prinzip kleine Kreisel. Die rotierende Raumzeit kann durch ein gravitomagnetisches Feld beschrieben werden. Der Shift-Vektor (β), wie er im ADM-Formalismus auftritt, kann als Vektorpotential angesehen werden, der dieses Feld im Raum erzeugt. Das Konzept ist vollkommen analog zur klassischen Elektrodynamik, wo das magnetische Vektorpotential A das Magnetfeld, B = rot A, erzeugt. Das Pendant zur Lorentz-Kraft heißt beim Frame-Dragging gravitomagnetische Kraft. Letztendlich beeinflusst diese Kraft Testkörper und zwingt ihnen die Korotation auf. Gyroskope werden dann zur Lense-Thirring-Präzession veranlasst. Es handelt sich bei dem Lense-Thirring-Effekt also physikalisch gesprochen um eine Wechselwirkung von Drehimpulsen, nämlich demjenigen des Loches (Kerr-Parameter a) und demjenigen des ankommenden Teilchens/Testkörpers/Kreisels.