Dieser Formalismus ist ein Konzept der klassischen und relativistischen Mechanik und bei der Behandlung allgemeiner mechanischer Probleme äußerst effektiv. Brandon Carter hat 1968 die Separabilität der Hamilton-Jacobi-Gleichung ausgenutzt, um eine vierte Konstante der Bewegung in der Kerr-Metrik herzuleiten: die Carter-Konstante.

Rezept: Carter-Konstante für Eilige

Zunächst – wie bei mechanischen Problemen üblich – muss man die Lagrange-Funktion L kennen. In der Relativitätstheorie gewinnt man sie aus der Metrik, die 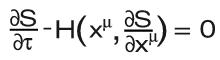als bekannt vorausgesetzt wird. Über eine Legendre-Transformation erhält aus L die Hamilton-Funktion H (Anmerkung: eine Legendre-Transformation ist eine Variablentransformation, die eindeutig L und H verknüpft). Dann liefert die Hamilton-Jacobi-Gleichung (siehe Gleichung rechts), die eine partielle, nicht-lineare Differentialgleichung erster Ordnung ist, eine Bestimmungsgleichung für eine Erzeugende, das Wirkungsfunktional S. Im Allgemeinen ist diese Differentialgleichung dann nur über einen Ansatz lösbar. Carters Verdienst war es, dass sein Separationsansatz, nämlich dass S in allen Koordinaten separiert, erfolgreich war. Die partiellen Ableitungen des nun bekannten Wirkungsfunktionals S liefern dann gerade die Photonenimpulse in einem speziellen Beobachtersystem, dem Bardeen-Beobachter oder ZAMO.

Anwendungsbereich

Während der Hamilton-Jacobi-Formalismus von genereller Wichtigkeit ist, benötigt man die Carter-Konstante nur in einem Spezialgebiet: so ist die Lösung der Geodätengleichung in der Kerr-Metrik über die vier Erhaltungsgrößen ein Standardverfahren, das vor allem für relativistisches Ray Tracing verwendet wird. Weil die Schwarzschild-Lösung (mit Drehimpuls null) nur ein Spezialfall der Kerr-Lösung ist, kann man das Verfahren auch für diese statische Raumzeit anwenden.