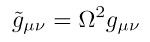In der Allgemeinen Relativitätstheorie (ART) benutzt man konforme (übersetzt eigentlich: 'gemeinsame Form') Transformationen, um sich ausgehend von einer gegebenen Metrik die zugehörige konforme Metrik zu beschaffen. In der Gleichung rechts sind Metrik (rechts) und konforme Metrik (links) über den konformen Faktor (Ω) miteinander verknüpft. Der konforme Faktor ist im Allgemeinen eine Funktion von verschiedenen Koordinaten. Als konformer Faktor geeignet ist beispielsweise die Arcus Tangens Funktion. Sie ordnet einem Intervall von -∞ bis +∞ einen Intervall von -π/2 bis +π/2 zu.
Sinn dieser Prozedur ist es, das Verhalten im Unendlichen von Metriken auf einen endlichen Bereich abzubilden. Die konforme Metrik hat per definitionem dieselben Eigenschaften, so dass die Ergebnisse dieser Untersuchung auf die Ausgangsmetrik übertragen werden dürfen.

Wozu braucht man das?

Die konforme Transformation ist ein wesentlicher Schritt, um von Raumzeiten das Penrose-Diagramm darzustellen. Geeignete konforme Faktoren führen so eine 'physikalische' Metrik auf eine 'unphysikalische', deren Studium das asymptotische Verhalten der physikalischen Metrik offenbart.