Die Loop-Quantengravitation (LQG), im Deutschen auch bisweilen Schleifen-Quantengravitation (auch Schleifenquantengravitation) genannt, ist eine Theorie der Quantengravitation. Damit wird bestrebt die Konzepte der Quantentheorie mit denjenigen der Allgemeinen Relativitätstheorie (ART) zu vereinigen. Anders gesagt, wird der Versuch unternommen, das Gravitationsfeld zu quantisieren. Das damit verbundene Gravitationsfeldquant nennt man in den Quantenfeldtheorien (QFT) Graviton. In der LQG distanziert man sich eher vom Begriff des Gravitons und bezeichnet die Quanten der Theorie als Loops (dt. Schleifen).

gekörnte Raumzeit

In der ART ist die Raumzeit ein deformierbares, vierdimensionales, kontinuierliches Gebilde, ein Raum-Zeit-Kontinuum, das durch Energieformen wie der Masse gekrümmt wird. Die klassischen Theorien sehen keine Prinzipien wie Unschärfe oder diskrete physikalische Größen (Quanten) vor. Die Raumzeit erscheint hinreichend glatt, kontinuierlich und weist allenfalls 'Löcher' in Form von Krümmungssingularitäten auf (die Schwarzen Löcher sind ein Beispiel dafür). Nun impliziert aber die Quantentheorie und im Speziellen die daraus mit der ART abzuleitende Planck-Skala, dass bei sehr starken Gravitationsfeldern auf sehr kleinen Längenskalen eine Körnung der Raumzeit auftauchen muss. Die Längenskala, wo die Körnung auftritt, ist im Bereich der Planck-Länge, also auf nur 10^-33 cm. Das ist die kleinste Längeneinheit, die Physiker kennen. Die Granulation, erfordert eine Theorie, die über die ART hinaus geht und dem quantenhaften Charakter der Raumzeit Rechnung trägt: eine Quantengravitation.

Erfolge quantisierter Feldtheorien

Lange Zeit gab es für diese Theorie nur einen ernst zu nehmenden Kandidaten, die Stringtheorien. Dies war im Wesentlichen dadurch motiviert, dass diese Theorien ein Teilchen mit Spin 2 (Tensorboson) enthalten. Gerade das war eine gewünschte Eigenschaft für das Graviton. Deshalb waren die Stringtheorien schlagartig attraktiv für eine quantisierte Gravitationstheorie. Der mathematische Apparat der Quantenfeldtheorien erwies sich als sehr erfolgreich zur Beschreibung von Elementarteilchen, wie die Quantenelektrodynamik, Quantenchromodynamik, elektroschwache Theorie, Große Vereinheitlichte Theorien, generell gesagt, die Eichtheorien belegen. Diese Konzeption offenbarte eine einheitliche Sicht in Form des Standardmodells der Teilchenphysik. Diesen Apparat der Quantenfeldtheorien versuchten die Theoretiker auch auf die Strings anzuwenden.

Strings & Branen

Es stellte sich heraus, dass fadenförmigen Strings morphologisch verallgemeinert werden können zu flächenhaften Gebilden, den Branen. Die Stringtheorien erfordern jedoch die Existenz von (räumlichen) Extradimensionen (sechs oder sieben weitere Raumdimensionen neben den bekannten dreien). Sie erfordern auch eine Gültigkeit der Supersymmetrie (SUSY), um mit dem physikalischen Prinzip der Kausalität vereinbar zu sein. Eine Gültigkeit der SUSY hat zur Konsequenz, dass die bis heute bekannten Teilchen des Standardmodells so genannte Superpartner haben. Der Teilchenzoo wird also signifikant vergrößert, viele neue SUSY-Teilchen müssen dann existieren. Aber: Bisher wurde keines dieser SUSY-Teilchen experimentell beobachtet, ebenso wenig weitere, räumliche Dimensionen neben den bekannten dreien.

Die Anfänge der Loop-Gravitationstheorie

Dies motivierte zur Suche nach alternativen Konzepten, die ganz andere Ansätze verfolgen, als die Stringtheorien; Konzepte, die nicht notwendig Extradimensionen und SUSY erfordern. Genau das ist die Loop-Quantengravitation, eine Theorie, deren Anfänge bis 1986 zurück reichen. In besagtem Jahr arbeiteten Amitaba Sen und Abhay Ashtekar an einer neuen Formulierung der ART mithilfe neuer mathematischer Variablen, die man Zusammenhänge (engl. connections) nennt. Das Christoffel-Symbol der ART (assoziiert mit den Einsteinschen Feldgleichungen und der kovarianten Ableitung), das anschaulich die Newtonsche Gravitationskraft in einer geometrischen Beschreibung der Gravitation ablöst, ist gerade mathematisch gesprochen ein Zusammenhang (Konnexion). In der Ashtekar-Formulierung der ART ist die Feldvariable nicht mehr die Metrik, sondern ein so genannter selbst-dualer Zusammenhang (der sich vom Christoffel-Symbol unterscheidet). Seither nennt man diese auch Ashtekar-Variablen.
Im gleichen Jahr, 1986, reformulierten Ted Jacobson und Lee Smolin die Wheeler-DeWitt-Gleichung in diesen neuen Variablen. Sie fanden auch eine Klasse von exakten Lösungen dieser Gleichungen: die Wilson-Loops (dt. Wilson-Schleifen). Um zu verstehen, was dies für mathematische Objekte sind, muss man weiter ausholen – leider wird es nun begrifflich recht kompliziert, weil eine Erklärung ohne Mathematik nicht angemessen ist. Der mathematisch weniger interessierte Leser mag den folgenden Abschnitt überspringen.

LQG in der Sprache der Mathematik: Holonomien und Wilson-Loops

Mit Holonomie bezeichnet man auch den Parallel-Propagator (Holonomie-Operator), also denjenigen Operator, der einen Parallel-Transport (eine Transformation, vergleiche auch Lie-Ableitung) eines Zusammenhangs, eines Vektors oder eines Tensors entlang einer geschlossenen Kurve auf einer Raumzeit (mathematisch eine Riemannsche Mannigfaltigkeit) bewerkstelligt. Holonomie genügt bestimmten mathematischen Eigenschaften, vor allem bildet sie eine mathematische Gruppe, die Holonomie-Gruppe.
Eine besondere Bedeutung hat nun die Spur des Holonomie-Operators (Summe der Diagonalelemente, wenn der Operator als Matrix dargestellt wird). Die Spur, bezogen auf einen bestimmten Pfad durch die Raumzeit, dient zur Bestimmung von parallel-transportierten physikalischen Größen, wenn ein Teilchen entlang des Pfads durch die Raumzeit propagiert.
Als Beispiel möge ein Elektron dienen, das sich durch die Raumzeit bewegt. Durch Anwendung des Parallel-Propagators, kann man untersuchen, wie sich die Observable Spin ändert. Die Krümmung der Raumzeit rotiert den Spinvektor bei der Bewegung entlang der geschlossenen Kurve. Berechnet man nun die Spur des zugehörigen Parallel-Propagators, so hat man ein Maß gefunden, wie sich die Observable Spin geändert hat. Als Anforderungen an die Kurven sei gestellt, dass sie 'glatt' seien und keine Überschneidungen aufweisen mögen.

Die Spur des Holonomie-Operators ist eichinvariant und ist gerade der Wilson-Loop.

Schon in der Betrachtung der QFTs als Eichtheorien erwiesen sich der Wilson-Loop bzw. Holonomien als die natürliche Basisvariablen und ermöglichten die Formulierung der Quantenchromodynamik (Yang-Mills-Theorie, einer Gitter-Eichtheorie). Die Eichtheorien erfuhren so eine tief liegende geometrische Interpretation (Gambini & Trias, 1981 und 1986). Auch in der Loop-Quantengravitation ist dieser Formalismus erfolgreich und gab dieser Theorie ihren Namen: Loop stammt verkürzend von Wilson-Loop. Die Wilson-Loops der Ashtekar-Zusammenhänge lösen also die reformulierte Wheeler-DeWitt-Gleichung.
Carlo Rovelli und Lee Smolin nutzten nun 1987 die Wilson-Loops als neue Basiszustände des separablen Hilbert-Raums der Quantengravitation. Physikalische Größen (Observablen) werden dann durch diese Loop-Basis dargestellt. Der Hilbert-Raum der Loops lässt sich im Vergleich zum Quantensystem des Harmonischen Oszillators der Quantenmechanik besser verstehen.

Einschub: harmonischer Oszillator

Beim harmonischen Oszillator geht man zunächst vom Hamilton-Operator (Hamiltonian) aus. Er enthält die Observablen Impuls und Ort als Operatoren. Man formuliert nun das Eigenwertproblem dieses Quantensystems, dessen Lösung Energieeigenwerte des Hamiltonians und Eigenzustände (Eigenfunktionen, Wellenfunktionen ) liefert. Man hat also das diskrete Spektrum des Operators gefunden. Die Energieniveaus benachbarter Eigenzustände im harmonischen Oszillator unterscheiden sich gerade um ein Oszillatorquant (Vibron), das eine diskrete Energie hat, das dem Produkt von Planckschem Wirkungsquantum und Oszillatorfrequenz entspricht. Mit einer natürlichen Zahl n kann man das diskrete Spektrum parametrisieren. Der Grundzustand, der Vakuumzustand des harmonischen Oszillators, hat gerade n = 0 und liefert einen endlichen Energieeigenwert, die Vakuumenergie des harmonischen Oszillators. Der n-te Eigenzustand enthält gerade n Oszillatorquanten. In der Feldtheorie der Elektrodynamik, der QED, die formal ähnlich zu konstruieren ist, heißen diese Teilchen Photonen. Die Quantisierung des elektromagnetischen Feldes ist jedoch ungleich komplizierter in ihren Details als die Quantenmechanik des harmonischen Oszillators (unter anderem wegen der Renormierungsprozedur).

quantisierter Raum: Volumenquanten

Die Hamilton-Jacobi-Theorie, die bereits in der klassischen Mechanik Anwendung findet, kann benutzt werden, um die Gestalt des Hamiltonians der LQG zu finden. Die Methode der LQG folgt prinzipiell dem gerade beschriebenen Konzept der Quantenmechanik (wenn man sich einen geeigneten Hamiltonian beschafft hat), beachtet dabei aber auch die Gesetzmäßigkeiten der Allgemeinen Relativität. Man kann dabei soweit gehen zu sagen, dass die lokale Messung von Längen, Flächen und Volumina einer Vermessung der lokalen Eigenschaften des Gravitationsfeldes gleich kommt. So stellt sich das Volumen in der LQG als Volumenoperator heraus, der eine nicht-lineare Funktion des Gravitationsfeldes bzw. der Metrik ist. Das Spektrum dieses Operators ist, analog wie oben beim Harmonischen Oszillator dargestellt, diskret, d.h. das Raumvolumen ist quantisiert in Volumenquanten. Dies sind die irreduziblen Elemente des Raums, die eine Volumen von 10^-99 Kubikzentimetern einnehmen (Planck-Länge hoch 3). Entsprechend finden sich im Universum, das einen Hubble-Radius (siehe dazu Horizont) von etwa 13.6 Mrd. Lichtjahren hat, 10¹⁸⁴ Volumenquanten! Damit befinden sich in einem Kubikzentimeter mehr Volumenquanten (10⁹⁹), als Kubikzentimeterwürfel im Universum (10⁸⁴)!
Die resultierende, körnige oder granulare Struktur der Raumzeit (engl. grains of space-time) auf der Planck-Skala ist ein wichtiges Ergebnis der Loop-Quantengravitation und wurde 1992 gefunden. Die LQG beschreibt demgemäß die kleinskalige Struktur der Raumzeit (engl. small scale structure of space-time) und erweitert die relativistische Kosmologie auf der mikroskopischen Skala. Die Körnung umschreibt man manchmal mit dem Begriff 'Raumzeitschaum'. Dieses Resultat der LQG steht in krassem Gegensatz zum Begriff Raum-Zeit-Kontinuum der Relativitätstheorie: die Raumzeit entpuppt sich auf den kleinen Quantenskalen als diskontinuierlich oder diskret.

quantisierter Raum: Flächenquanten

Nun befindet sich zwischen benachbarten Raumvolumina eine gemeinsame Fläche mit bestimmtem Flächeninhalt (engl. area). Der Flächeninhalt ist ebenso abhängig vom Gravitationsfeld und quantisiert wie das Volumen, nämlich in Flächenquanten. Ihre Ausdehnung ist gerade das Quadrat der Planck-Länge, also 10^-66 Quadratzentimeter. Ihr Daumennagel besteht also aus 10⁶⁶ dieser Flächenquanten, die Erdoberfläche aus 10⁸⁵. Man kann sich nun im Allgemeinen einen Quantenzustand, der aus n Volumenquanten bestehen möge, als einen so genannten Graphen vorstellen, der Knoten aufweist. Das Teilgebiet der Mathematik, das sich damit auseinander setzt, heißt Knotentheorie. Die Knoten entsprechen gerade den Volumenquanten; benachbarte Volumenquanten sind durch Flächenquanten 'verbunden'.

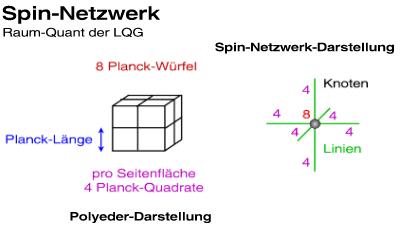
Spin-Netzwerke

Die gerade beschriebene Struktur nennen die Theoretiker Spin-Netzwerk. Man kann diesen Gebilden Quantenzahlen zuordnen, die gerade mit den Volumen- und den Flächenquanten assoziiert sind. Dies ist schematisch in der Abbildung oben dargestellt: Wir zerlegen den dort gezeigten Polyeder, ein dreidimensionaler 'Vielflächner', in Volumenquanten. Im Beispiel ist dies für einen Würfel geschehen, der aus acht Volumenquanten bestehen möge. Die Darstellung dieses Gebildes als Spin-Netzwerk geschieht nach dem folgenden Algorithmus: Wir skizzieren einen Knoten und versehen ihn mit einer Zahl, die der Anzahl seiner Volumenquanten entspreche, in diesem Fall acht. Für jede Berandungsfläche des Polyeders zeichnen wir dann eine (beliebig lange) Linie, im Beispiel also sechs Linien. Die Zahlen an diesen Linien geben die Anzahl der Flächenquanten der jeweiligen Seite an, in diesem Beispiel immer vier. Dies bildet das einfache Spin-Netzwerk in der Abbildung rechts dargestellt.
Beliebige Volumina lassen sich so als komplizierte Spin-Netzwerke darstellen. In der LQG ist es nun auch möglich Spin-Netzwerke ohne Pendant in der Polyederdarstellung zu generieren. In Spin-Netzwerken sind nur die Quantenzahlen und die relativen Verknüpfungen relevant. Sie enthalten die Information über den quantisierten Raum.

Die Entdeckung der Spin-Netzwerke (engl. spin network) in der LQG war ein wichtiger Schritt für die Theorie (Rovelli & Smolin 1995). Der Begriff Spin-Netzwerk wurde jedoch bereits 1971 von dem englischen Relativisten und Mathematiker Roger Penrose eingeführt, mit der Absicht Mannigfaltigkeiten (in der ART sind das Raumzeiten) eher von einem kombinatorischen Standpunkt zu sehen. Bevor die Spin-Netzwerke Einzug in die LQG fanden, wurden die Loops und Multiloops (ein Zustand aus vielen Loops, die auch überlappen können) als Basiszustände für den Hilbertraum der Theorie herangezogen. Es ist wie in der Quantentheorie: einen beliebigen Quantenzustand kann man in Basiszuständen ausdrücken. Wem das noch nichts sagt: Es verhält sich so ähnlich wie mit beliebigen Zahlen, die man in Potenzen der Zahl 10 zerlegen kann: 123 = 1 × 10² + 2 × 10¹ + 3 × 10⁰.

Spin-Netzwerke stellen eine neue, orthonormale Basis dar.

Sie weisen gegenüber den Loop-Zuständen rechentechnische Vorteile auf. So diagonalisieren Spin-Netzwerk-Zustände den Flächen- und Volumenoperator, was sie 'mathematisch handlicher' macht.

quantisierte Zeit

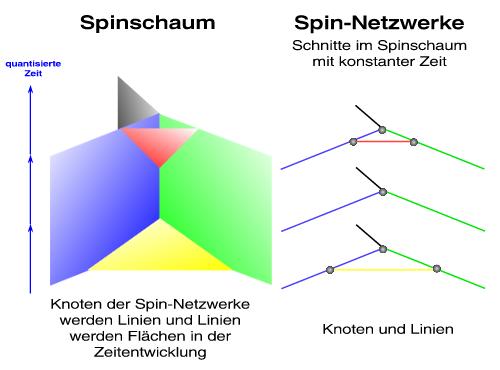
Es wäre nun zu vereinfachend anzunehmen, dass der Raum aus kleinen Polyedern besteht. Dieser Ansatz trägt der Krümmung des Raumes nicht Rechnung. Außerdem wurde in der bisherigen Betrachtung die Zeitkoordinate vernachlässigt, die doch in der ART ein vernetztes Kontinuum mit den drei Raumrichtungen bildet. Man muss also den Spin-Netzwerken eine zeitliche Entwicklung zugestehen. Wie soll das gehen? Man muss sich das so vorstellen, dass durch diese Entwicklung Knoten im Spin-Netzwerk verschwinden, neue auftauchen, neue Verbindungen geknüpft und alte aufgelöst werden. Ein solches Gebilde heißt Spinschaum (engl. spin foam) und ist in der nächsten Abbildung unten illustriert. Durch die zeitliche Entwicklung werden die Knoten der Spin-Netzwerke zu Linien im Spinschaum, ebenso werden die Linien im Spin-Netzwerk zu Flächen im Spinschaum. In der Abbildung wird eine Zeitrichtung angegeben. Die Zeit sei jedoch auch quantisiert in den fundamentalen Einheiten der Planckzeit, also in 'Zeitpaketen' von 10^-43 Sekunden. Damit sei die Zeit in der LQG nicht der sprichwörtliche, kontinuierliche Fluss, sondern eher vergleichbar mit dem Ticken einer Uhr:

Wie der Zeiger auf dem Ziffernblatt der Uhr mache die Zeit Sprünge!

Bei diesen 'Zeitsprüngen' ändert sich die Gestalt des Spin-Netzwerkes schlagartig, instantan. Diese Entwicklung wird sichtbar, wenn man den Spinschaum (in der Abbildung links dargestellt) entlang der Zeitachse in Spin-Netzwerke zerlegt (in Abbildung rechts dargestellt). Mit jedem Zeitquant reformiert sich das Spin-Netzwerk. Oder anders gesagt: Überall dort, wo sich ein ein Spin-Netzwerk neu formiert, tickt einmal eine lokale Uhr!

Überall & nirgendwo

Das erinnert an den ADM-Formalismus (3+1 Split) der ART, wo man die vierdimensionale Raumzeit in dreidimensionale (räumliche) Hyperflächen mit jeweils konstanter Zeit auffächert. Zeitentwicklung kommt dadurch zustande, dass man sich entlang des Shift-Vektors der Raumzeit von einer zur nächsten Hyperfläche bewegt. Dieses so genannte Slicing (Foliation, Blätterung) ist wesensgleich mit der Zerlegung des Spinschaums in der LQG.
Die Darstellung von Spinschaum wird häufig mit den Feynman-Diagrammen der Quantenfeldtheorien verglichen. Hier ist jedoch Vorsicht geboten! Feynman-Diagramme enthalten eine Zeit und eine Raumachse, die man üblicherweise weglässt. Im Prinzip gibt es das beim Spinschaum nicht. Ein Spin-Netzwerk ist ein fixierter Quantenzustand mit bestimmtem Volumen und bestimmter Fläche. Zeit ist ein lokales Phänomen und mit einer Umordnung der Knoten- und/oder Linienstruktur des Spin-Netzwerks verbunden. Anders gesagt: In der Loop-Quantengravitation ist die Raumzeit (Newton: das Gravitationsfeld) eine Superposition (Überlagerung) von Spin-Netzwerken, so wie das elektromagnetische Feld in der Quantenelektrodynamik eine Superposition von Photonen ist. Das Erstaunliche ist nun, dass ein Spin-Netzwerk-Zustand nicht lokalisierbar ist, er hat also keinen definierten Ort! In diesem Sinne ist er abstrakt und nicht auf einer raumzeitlichen Mannigfaltigkeit definiert. Wie kommt es zu dieser seltsamen Eigenschaft?

Hintergrundunabhängigkeit

Letztendlich hat man diese seltsame Eigenschaft als Forderung in die Theorie hinein gesteckt. Die Eigenschaft trägt den Namen Hintergrundunabhängigkeit und ist die wichtigste Eigenschaft der LQG. Historisch gesehen wurde sie von der ART antizipiert und jeder kovarianten Quantengravitation impliziert. Die Geometrie der Raumzeit ist in der ART dynamisch, d.h. der Hintergrund ist nicht statisch, sondern verändert sich durch den Einfluss von sich bewegenden Massen und Energien. Ein anderer Aspekt der Hintergrundunabhängigkeit ist, dass die Wahl des Koordinatensystems frei ist. Das folgt aus dem Kovarianzprinzip, denn die Tensoren der ART sind koordinatenunabhängig. Mathematisch fasst man diese Eigenschaft mit einer Unabhängigkeit der Theorie von 'Verschiebungen' auf der Mannigfaltigkeit. Allgemein nennt man Abbildungsvorschriften in der Mathematik Morphismen. Sie sind Gegenstand der Kategorietheorie, einer Teildisziplin der Mathematik. Die Unabhängigkeit vom Hintergrund nennt man mathematisch Diffeomorphismusinvarianz. Der Diffeomorphismus ist eine Abbildung, die gerade die Verschiebung auf der Mannigfaltigkeit bewerkstelligt. Trotz dieser Verschiebung, darf sich aber die Physik nicht ändern; das diktiert die ART.
Abstrahiert man zwei Spin-Netzwerke als Graphen, so können sie über den Diffeomorphismus ineinander überführt werden. Die Diffeomorhismusinvarianz besagt nun, dass diese beiden Spin-Netzwerke eich-äquivalent sind, also die gleiche Physik beschreiben. Diese Äquivalenz ist wesensgleich zur Äquivalenz zweier Lösungen der Einstein-Gleichungen der ART (z.B. der Kerr-Lösung), die sich nur in der Wahl der Koordinaten unterscheiden (z.B. Boyer-Lindquist-Koordinaten gegenüber Kerr-Schild-Koordinaten): beide Lösungen beschreiben dasselbe Objekt (in diesem Beispiel ein rotierendes, ungeladenes Schwarzes Loch), also dieselbe Physik. Dies führt sogar auf die folgende Aussage:

Das Spin-Netzwerk ist nicht in der Raumzeit, es ist die Raumzeit!.

Allerdings 'leben' dynamische Objekte wie Teilchen des Standardmodells auf Spin-Netzwerken. Teilchen und Felder in Spin-Netzwerken geben den Knoten und Linien weitere Quantenzahlen. Die Veränderung der Quantenzahlen im Spin-Netzwerk entlang eines Graphen symbolisiert gerade die Bewegung des Teilchens durch die Raumzeit. 1994 wurde die Kopplung von Materie (insbesondere Fermionen) an die bis dato materiefreie LQG untersucht. Beide orthonormale Basen, Loop-Basis wie Spin-Netzwerk-Basis, dienen also als mathematische Darstellung von hintergrundunabhängigen, physikalischen Größen (Diffeomorphismusinvarianten).
Die neue Formulierung in Spin-Netzwerken brachte der LQG den alternativen Namen Quantenspindynamik (QSD) ein. Manchmal spricht man auch von der Quantengeometrie, wegen des tiefen geometrischen Aspekts, den diese Quantengravitation von der ART geerbt hat.

Strings vs. Loops

Die LQG wird gewöhnlich in vier Dimensionen und ohne Supersymmetrie formuliert. Sie ist zwar kompatibel mit diesen Konzepten, benötigt sie aber a priori nicht. Dies ist der gewichtigste Unterschied zu den Stringtheorien. Bisher gibt es keinerlei experimentelle Evidenz für zusätzliche Raumdimensionen und supersymmetrische Teilchen. Diese empirische Beobachtung spricht deshalb besonders für die LQG bzw. Theorien ohne Extradimensionen und ohne Supersymmetrie.
Auch zielt die LQG noch nicht so sehr auf eine Unifikation aller vier Wechselwirkungen, die es in der Natur gibt, sondern lediglich auf eine Quantisierung der Gravitation unter strenger Berücksichtigung der erfolgreichen Konzepte der ART. In diesem Sinne ist sie vom Standpunkt des Relativisten ein 'natürlicher' Zugang zur Quantengravitation, als wenn man sich der Herausforderung von der Seite der Quantenfeldtheorien nähert. Anders gesagt: Die LQG 'will weniger', da sie nicht im Unifikationsgeist einer Theorie von Allem (engl. Theory of Everything, TOE) steht. Es ist aber nicht auszuschließen, dass sich Konzepte der LQG auf eine TOE anwenden lassen.

experimentelle Tests der LQG

Eine wichtige Eigenschaft einer Theorie ist ihre Falsifizierbarkeit. Die Wissenschaftstheorie besagt, dass man eine Theorie niemals beweisen, sondern nur widerlegen kann (Buch von Karl R. Popper: Logik der Forschung). Vor dem Ruhm einer Theorie steht die Bewährung: Die Physiker testen die Prognosen einer Theorie immer wieder in physikalischen Experimenten. Erst wenn die Theorie immer wieder übereinstimmende Resultate mit dem Experiment (in der Astronomie sind das astronomische Beobachtungen) liefert, so hat sie sich bewährt. Stringtheorien und LQG müssen sich noch bewähren. Welche Vorhersagen macht die LQG und wie kann man sie testen?

• Von prinzipiellem Interesse ist die Physik auf der Planck-Skala. Die Granulation der Raumzeit sollte hier – stimmen LQG im Speziellen und Anforderungen an eine Quantengravitation im Allgemeinen – nachweislich zu Abweichungen führen. Vielleicht gelingt ein experimenteller Aufbau zum (direkten oder indirekten) Nachweis der Volumenquanten der LQG, auch wenn die assoziierte Skala außerordentlich klein ist. Derzeit ist die klassische Planck-Skala unerreichbar mit direkten Experimenten wie z.B. mit Teilchenbeschleunigern.
• Eine theoretische Ableitung der Bekenstein-Hawking-Entropie, die sich relevant für die ThermodynamikSchwarzer Löcher zeichnet, ist auch in der LQG möglich. Die Stringtheorien erlauben eine Berechnung, die zum selben Ergebnis führt. Vom theoretischen Standpunkt ist dieses Resultat beruhigend, aber sicher keine starke Stütze der Theorie. Erschwerend kommt hinzu, dass die Bekenstein-Hawking-Entropie selbst noch nicht experimentell untermauert wurde, sondern nur in ganz verschiedenen Theorien übereinstimmend vorkommt. Das Attraktive an der LQG-Rechnung ist, dass sie eine neue, mikroskopische Interpretation der Bekenstein-Hawking-Entropie auf den Tisch bringt: diese Entropie resultiert, indem man die Anzahl der Eigenzustände des Flächenoperators (s.o. Flächenquanten) auf dem Horizont zählt.
• In der Optik sind neue Effekte zu erwarten. Während das gewöhnliche optische Vakuum nicht-dispersiv ist, sollte infolge der Granulation der Raumzeit, wie sie die LQG beschreibt ein dispersives Vakuum resultieren. Dispersion heißt in der Optik, dass die Vakuumlichtgeschwindigkeit (Symbol c) von der Farbe abhängt. In der klassischen Elektrodynamik kann man gerade die Wellengleichung der Strahlung (unquantisiert) ableiten, wie sie in die Optik eingeht. Gambini & Pullin haben 1998 die klassische Elektrodynamik mit den Konzepten der LQG reformuliert und eine modifizierte Wellengeschwindigkeit abgeleitet. In einem c-Test könnte man nun experimentell überprüfen, ob die Lichtgeschwindigkeit auf der Skala von Minuten – wie sie vorhersagen – tatsächlich für unterschiedliche Farben abweicht. Es wurde vorgeschlagen diesen Sachverhalt mit Gamma Ray Bursts in kosmologischen Distanzen zu überprüfen. Der elektromagnetische Schauer dieser kosmischen Strahlungsausbrüche, der im GRB-Nachleuchten (engl. afterglow) auf allen Spektralbereichen auftritt, eignet sich hervorragend zum c-Test, weil die geringen Unterschiede in der Ausbreitungsgeschwindigkeit kumuliert werden und bei den hohen Entfernungen kosmologischer GRBs deutlich zu Tage treten sollten. Bislang gibt es keine Resultate dieses Experiments. Erste Ergebnisse erhofft man sich von der GRB-Mission GLAST.

c ≠ const

Die nichtuniverselle Lichtgeschwindigkeit der LQG stellt Einsteins Spezielle Relativitätstheorie (SRT) in Frage! Es existieren bereits Modifizierungen der SRT, dass die Lichtgeschwindigkeit eben nur im Limit hoher Wellenlängen (kleiner Photonenenergien) gilt. Ob 'die heilige Kuh der Physiker' geschlachtet werden muss und die Lichtgeschwindigkeit doch nicht konstant ist, müssen präzise Experimente ergeben.

Loop-Quantengravitation und Kosmologie

Mit den Methoden der Loop-Quantengravitation lässt sich auch Kosmologie betreiben. Diese Disziplin heißt in der Literatur Loop-Quantenkosmologie (Loop Quantum Cosmology, LQC). Einige LQG-Rechnungen zeigen bereits entscheidende Konsequenzen für die Kosmologie:

• Das Universum habe laut LQG im Urknall eine Mindestgröße. Es gäbe nach dieser Vorstellung also keine Urknall-Singularität! Das Big-Bounce-Modell der Kosmologie (Priester & Blome, 1991) erlebt so die Wiederbelebung mit neuer Physik (Bojowald, AEI Golm, 2003, s.u.).
• Der kosmologische Skalenparameter der Friedmann-Weltmodelle (symbolisiert durch a(t) oder R(t)) parametrisiert die Entwicklung des Universums in der Art eines Zeitparameters. Weil das Volumen des Universums gemäß LQG quantisiert ist, sei es auch der Skalenparameter und die (kosmologische) Zeit! Die kosmologische Entwicklung sei daher diskret.
• Eine besonders interessante Implikation hat die LQG auf die Inflation, einer exponentiellen Expansionsepoche im frühen Universum. In der LQG benötigt man kein hypothetisches Skalarfeld, genannt Inflaton, um die anfänglich überlichtschnelle Expansion der Inflationsära zu treiben. Die exponentielle Ausdehnung sei allein eine Folge der Quanteneigenschaften der Raumzeit!

LQG-Kollapsrechnungen

Sehr interessante Arbeiten sind in den Jahren 2005 und 2006 zum Gravitationskollaps im Rahmen der LQG erschienen (Bojowald et al. 2005, Goswami et al. 2006). Im Kern zeigen diese vorläufigen Rechnungen, dass die Ausbildung einer Singularität verhindert werden kann. Wie funktioniert das?
Zunächst erinnert das Vorgehen an die ersten rein relativistischen Kollapsrechnungen in den 1930er Jahren: zur Vereinfachung nehmen die Physiker den homogenen und isotropen Fall an. Sie betrachten nun ein Skalarfeld, das in sich zusammenfallen möge. Das Skalarfeld steht dabei für eine einfache Form von Materie (wir erinnern uns, dass z.B. das Higgs-Boson, die Kaonen und die Pionen skalare Bosonen mit Spin 0 sind). Interessanterweise war es den Theoretikern möglich, die FLRW-Metrik der Kosmologie zur Beschreibung des Kollapses im Innern zu benutzen. Aber hier kommen die Loop-Effekte ins Spiel: diese Metrik wird granular. Eine Quantisierung der Raumzeit wird dann wichtig, wenn der Skalenfaktor a(t) vergleichbar wird mit einem kritischen Wert a_∗, der durch die LQG festgelegt wird. Fuer a » a_∗ liegt der klassische, relativistische Fall vor, wo die granulare Raumzeit irrelevant ist. Goswami et al. betrachten nun den interessanten Fall a « a_∗ und setzen den Hamiltonian der LQG an. Zur Erinnerung: Der Hamiltonian ist der Energieoperator der Quantentheorie, dessen Spektrum (die Eigenwerte) etwas über die diskreten, energetischen Zustände des Systems verrät.
Interessant ist nun die zeitliche Entwicklung des Skalarfelds im Kollaps. Dieser Vorgang wird durch eine Bewegungsgleichung des Skalarfelds Φ beschrieben, die in der Quantenfeldtheorie allgemein Klein-Gordon-Gleichung heißt. Die Diskussion der Dynamik dieses Feldes zeigt, dass der Kollaps aufgehalten werden kann und ein Radius null ('die Singularität') nicht erreicht wird. Weiterhin zeigt sich, dass die Energiedichte des Feldes nicht unendlich wird. Konsequenz: Die Quantisierung der Raumzeit verhindert die Ausbildung von Singularitäten!
Wer drückt dagegen? Wir wissen ja von anderen kompakten Objekten, dass sich irgendein Druck dem mächtigen Gravitationsdruck im Kollaps entgegenstellen muss, damit der Kollaps auf ein Schwarzes Loch aufgehalten werden kann. Goswami et al. untersuchten den effektiven Druck des Feldes und konnten zeigen, dass dieser im Regime a « a_∗negativ wird. Ein negativer Druck wirkt ja wie die Dunkle Energie in der Kosmologie antigravitativ. Der negative Druck ist sogar so stark, dass er einen Massenverlust nach außen antreibt.
Sehr aufregend ist der Umstand, dass diese LQG-Kollapsrechnungen im Prinzip astronomisch beobachtbar sind! Denn der Massenverlust im Kollaps sollte Variationen in der Lichtkurve des Kollapsars bewirken. Sicherlich wird dieser Nachweis nicht leicht sein, zumal beim Sternenkollaps immer auch Massenverluste auftreten und darüber hinaus die Natur komplizierter ist, als in diesem Modell angenommen wurde. So zeigen Computersimulationen von Supernovae Typ II, dass diese vorzugsweise anisotrop und inhomogen sind. Dennoch sind die Loop-Rechnungen sehr ermutigend, zeigen sie doch, dass die Natur eventuell ohne Singularitäten auskommt.

Der Stand der Dinge

Der aktuelle Stand ist, dass sowohl LQG als auch Stringtheorien erstaunliche und neue Konzepte für das Verständnis von Raum und Zeit bieten. Leider gibt es bisher keinerlei experimentelle Hinweise, die die eine oder andere Theorie favorisieren würden. Deshalb stellt sich die aktuelle Situation so dar, dass beide Theorien richtig (im Sinne von nicht falsifizierbar), nur eine von beiden richtig oder gar beide falsch sein könnten! Die bisherige Nichtnachweisbarkeit von Extradimensionen und Supersymmetrie lassen die LQG attraktiver erscheinen, weil sie ohne diese Konzepte auskommt.
Eine aktuelle Entwicklung zeigt sogar auf eine Verknüpfung von LQG und Stringtheorien ohne Extradimensionen und ohne Supersymmetrie (Thiemann 2004). Der Einfachheit halber ist dieser Zugang zunächst beschränkt auf einen geschlossenen, bosonischen String auf flacher Minkowski-Geometrie. Die Bedeutung des LQG-Strings für die Physik bleibt abzuwarten.
Eine Entscheidung könnte auch die Lorentzinvarianz herbeiführen: In der ART ist diese Symmetrie erfüllt. Die moderne Forschung deutet an, dass die Lorentzinvarianz unter Umständen verletzt sein könnte. Auf der Grundlage astronomischer Beobachtungen werden die Bedingungen für Lorentzinvarianz derzeit erforscht. Vielleicht hilft dieser Sachverhalt eines Tages, um eine geeignete Quantengravitation – Stringtheorien, LQG oder etwas ganz anderes – auszuwählen bzw. aufzufinden.
Wer sich über das Für und Wider der LQG eine eigene Meinung bilden mag, dem seien die unten verlinkten, relativ verständlichen Papiere Loop Quantum Gravity: An Outside View von Nicolai et al. (2005) und Loop Quantum Gravity: An Inside View von Thiemann (2006) empfohlen.

Das letzte Wort hat jedoch – wie immer in der Physik – das Experiment.

Webtipps

• Artikel auf Einstein online: Die gebändigte Dichte von Martin Bojowald (AEI Golm) – sehr verständlich; über die kosmologische Rolle der LQG
• Website: Carlo Rovelli, einer der LQG-Pioniere, bietet auf seiner Homepage einige Materialien an.

Publikationen

• Baez: Spin Network States in Gauge Theory; gr-qc/9411007, 1994
• Rovelli & Smolin: Spin Networks and Quantum Gravity; gr-qc/9505006, 1995
• Rovelli: Loop Quantum Gravity; living reviews of relativity, 1997
• Gambini & Pullin: Non-standard Optics from quantum spacetime; gr-qc/9809038, 1998
• Smolin: How far are we from the quantum theory of gravity?; hep-th/0303185, 2003 (review)
• Rovelli: A dialog on quantum gravity; hep-th/0310077, 2003 (sehr unterhaltsam!)
• Smolin: Atoms of Space and Time; Scientific American, Januar 2004 (leicht verständlich)
• Thiemann: The LQG-String: Loop Quantum Gravity Quantization of String Theory; hep-th/0401172, 2004
• Bojowald et al.: A black hole mass threshold from non-singular quantum gravitational collapse; gr-qc/0503041, 2005
• Goswami et al.: Quantum Evaporation of a Naked Singularity; gr-qc/0506129, 2005
• Nicolai et al.: Loop Quantum Gravity: An Outside View; hep-th/0501114, 2005
• Thiemann: Loop Quantum Gravity: An Inside View; hep-th/0608210, 2006