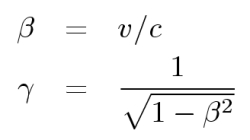Der Lorentz- oder Γ-Faktor (Gammafaktor) ist eine der wichtigsten dimensionslosen Größen in der Relativitätstheorie. Dieser Faktor hängt ausschließlich von der Relativgeschwindigkeit v ab. Dimensionslos wird der Lorentz-Faktor dadurch, dass die Geschwindigkeit v in der natürlichen Einheit der Relativitätstheorie, der Vakuumlichtgeschwindigkeit c gemessen wird. Im Vakuum bewegt sich das Licht mit 2.99792458 × 10⁸ m/s. Das Verhältnis von Relativ- zu Lichtgeschwindigkeit wird üblicherweise mit dem griechischen Buchstaben β bezeichnet.

Γ als relativistisches Maß

Der Γ-Faktor steigt sehr stark mit Erhöhung der Geschwindigkeit an. Im Grenzwert v = c, divergiert der Lorentz-Faktor und geht gegen unendlich! Die folgenden Links verweisen auf Diagramme, in denen die Abhängigkeit des Lorentz-Faktors von der Relativgeschwindigkeit dargestellt wird:

• v/c zwischen 0 und 1,
• v/c größer 0.9,
• v/c größer 0.99.

Die Relativgeschwindigkeit ist ein Vektor v und gibt die relative, unbeschleunigte Bewegung von zwei Bezugssystemen zueinander an. So kann man beispielsweise die Geschwindigkeit eines schnellen Teilchens betrachten. Die beiden Bezugssysteme sind einmal das uns vertraute Laborsystem. So nennen Physiker das Bezugssystem, in dem man das sich bewegende Teilchen untersucht. Zum andern gibt es das Ruhesystem des Teilchens, in dem das Teilchen sich nicht bewegt; der Beobachter 'sitzt' sozusagen auf dem Teilchen. Die Relativgeschwindigkeit gibt nun an, wie sich das Ruhesystem gegenüber dem Laborsystem bewegt.
Bei einer Betrachtung in einer Raumdimension, bewegen sich beide Systeme in dieselbe Richtung, aber unterschiedlich schnell. Dann reicht es, diesen Unterschied mit der Relativgeschwindigkeit v anzugeben, die in diesem Spezialfall nur einen Betrag hat und ein Skalar ist. Im Allgemeinen bewegen sich Ruhesystem und Laborsystem allerdings in unterschiedliche Richtungen und der Vektorcharakter der Relativgeschwindigkeit muss berücksichtigt werden. In den Lorentz-Faktor geht der Betrag v dieses Vektors v ein, den man gemäß der Vektorrechnung nach der Formel v² = |v|² = v_x²+ v_y²+ v_z² erhält. (Hier wurde ein Kartesisches Koordinatensystem {x,y,z} gewählt, um die Komponenten der Geschwindigkeit anzugeben. Die Geschwindigkeit kann jedoch in einem beliebigen anderen Koordinatensystem dargestellt werden.)

Wozu benötigt man den Lorentz-Faktor?

Einerseits dient er dazu, um einzuschätzen, wie relativistisch eine Bewegung ist. Es geht also um die Frage, ob die Bewegung des betrachteten Objekt bereits so schnell ist – nämlich vergleichbar schnell mit der Bewegung des Lichts – dass Effekte der Speziellen Relativitätstheorie eine Rolle spielen und berücksichtigt werden müssen. Diese Effekte sind die Zeitdilatation und die Lorentz-Kontraktion (oder Längenkontraktion): Länge und Zeitablauf hängen davon ab, wie schnell sich das betrachtete Objekt bewegt!
Es hat sich folgende Bezeichnungsweise eingebürgert, die klassifiziert, wie relativistisch eine Bewegung ist:

• Lorentz-Faktor gleich oder vergleichbar 1: nicht-relativistisch (engl. non-relativistic),
• Lorentz-Faktor größer als 2: relativistisch (engl. relativistic),
• Lorentz-Faktor größer als 10: 'mittelrelativistisch' (engl. mid-relativistic),
• Lorentz-Faktor größer als 100: ultrarelativistisch (engl. ultra-relativistic).

Lorentz-Transformationen

Andererseits geht der Lorentz-Faktor wesentlich in die Lorentz-Transformationen, den so genannten Boosts ein. Die Lorentz-Transformation vermittelt zwischen Ruhesystem und Laborsystem. Möchte man die relativistische Bewegung eines Teilchens im einen System vergleichen mit der im anderen System, so führt man die Lorentz-Transformation aus.
Außerdem gewichtet der Γ-Faktor die relativistischen Effekte Zeitdilatation und Längenkontraktion: Je größer Γ ist, umso ausgeprägter sind relativistische Phänomene. Dabei geht die geht die relativistische Mechanik stetig in die nicht-relativistische, die klassische oder Newtonsche Mechanik über. Die in der Physik schon viel länger bekannten Gesetze der klassischen Mechanik sind als Grenzfall in der relativistischen Mechanik enthalten. Das quantifiziert gerade der Lorentz-Faktor, weil er im Newtonschen Grenzfall sehr klein wird und gegen eins konvergiert. Das illustriert das erste Diagramm oben bei kleinen Geschwindigkeiten v.

Teilchenphysik: große Γs

In der Teilchenphysik sind relativistische Effekte an der Tagesordnung: In Teilchenbeschleunigern erreichen die beschleunigten Teilchen (Elektronen, Positronen, Protonen, Atomkerne) relativistische Geschwindigkeiten. Die relativistischen Effekte müssen bei den Beschleunigungsvorgängen berücksichtigt werden, so z.B. die Lorentz-Kontraktion der Atomkerne bei einer Kollision.

große Γs in der Astronomie

In der Astronomie gibt es eine Reihe sehr energetischer Prozesse, die hohe Lorentz-Faktoren involvieren. So bewegt sich in der Nähe eines Schwarzen Loches der Akkretionsfluss relativistisch schnell, ebenso die Jets, die aus der Zentralregion von Aktiven Galaktischen Kernen oder kompakten Objekten beschleunigt werden. Am Entstehungsort der Jets (dem so genannten Fußpunkt) sind typische Lorentz-Faktoren unterhalb von 10. Extreme Geschwindigkeiten wurden bei Gamma Ray Bursts beobachtet, die auf Γ-Faktoren bis 1000 schließen lassen.
Rekordhalter im Universum sind wohl die Pulsare: Die magnetisch getriebenen Pulsarwinde erreichen durch Nachbeschleunigung Lorentz-Faktoren bis 10000000! Ein prominentes Beispiel dafür, der Crabnebel im Sternbild Stier, wird im Lexikoneintrag SNR beschrieben.