Penrose-Diagramme, die in kompletter Bezeichnung eigentlich Carter-Penrose-Diagramme heiß sind unerlässliche Werkzeuge, um in der Allgemeinen Relativitätstheorie (ART) die Struktur einer Raumzeit im Unendlichen, insbesondere ihre kausale Struktur, zu untersuchen.

Die Grundidee

Diese Technik wurde vom brillanten Mathematiker und Relativisten Roger Penrose 1964/65 entwickelt. Dabei dient eine spezielle mathematische Operation, die konforme Transformation, dazu, um sich eine konforme Metrik aus der zu untersuchenden Raumzeit zu beschaffen. Die Eigenschaften der Metriken sind aufgrund der Konformität übertragbar.

konforme Transformation

Das Penrose-Diagramm ist dann im Prinzip ein Raumzeit-Diagramm der konform kompaktifizierten Raumzeit. Das klingt komplizierter, als es ist: Kompaktifizierung bedeutet in diesem Zusammenhang, dass eine unendlich ausgedehnte, physikalische Raumzeit auf eine 'unphysikalische' Raumzeit in ein endliches Gebiet transformiert wird. Bei der Transformation bildet man vereinfacht gesagt unendliche Intervalle auf endliche Intervalle ab.

Wie geht's weiter?

Penrose-Diagramme werden studiert, indem man den Verlauf von Teilchenbahnen verfolgt: wo beginnen sie, wo enden sie? Diese Bahnen nennt man in der ART Geodäten. Die Relativitätstheoretiker unterscheiden zeitartige Geodäten, denen Teilchen und Beobachter mit endlicher Ruhemasse folgen; Nullgeodäten, die von elektromagnetischer Strahlung (Photonen, die Lichtquanten, haben verschwindende Ruhemasse) genommen werden und raumartige Geodäten, die 'unphysikalisch' bzw. tachyonisch sind, weil sie die Kausalität verletzen. Diese Geodäten werden in das Penrose-Diagramm eingezeichnet, um zu verstehen, wie sich die Teilchen in der Raumzeit bewegen.

verschiedene Unendlichkeiten

Die Nomenklatur in Penrose-Diagrammen ordnet bestimmten Punkten und Flächen im Diagramm ein Symbol zu. Sie sind assoziiert mit unterschiedlichen Typen von Unendlichkeiten:

• Die vergangene zeitartige Unendlichkeit ist ein Gebiet, wo die Zeitkoordinate gegen negativ unendlich geht, während die Raumkoordinate endlich bleibt. Hier beginnen zeitartige Geodäten. In der Symbolik wird dies mit einem großen oder kleinen Buchstaben i mit Index – gekennzeichnet.
• Die zukünftige zeitartige Unendlichkeit ist ein Gebiet, wo die Zeitkoordinate gegen positiv unendlich geht, während die Raumkoordinate endlich bleibt. Hier enden zeitartige Geodäten. In der Symbolik wird dies mit einem großen oder kleinen Buchstaben i mit Index + gekennzeichnet.
• Die raumartige Unendlichkeit ist ein Gebiet, wo die Raumkoordinate gegen positiv unendlich geht, während die Zeitkoordinate endlich bleibt. Bis hier erstrecken sich raumartige Flächen. In der Symbolik wird dies mit einem großen oder kleinen Buchstaben i mit Index 0 gekennzeichnet.

Diese bisher genannten Unendlichkeiten treten typischerweise als Punkte in Penrose-Diagrammen in Erscheinung, weil höhere Dimensionen oft aus Gründen der Überschaubarkeit unterdrückt werden.
Daneben gibt es auch Gebiete, die in Penrose-Diagrammen wie Kanten aussehen und an sich Flächen sind. Sie werden mit einem besonderem Symbol versehen: dem großen Skript-I. Relativisten sprechen es wie 'skrai' aus, was ein Neologismus ist, der aus der phonetischen Verkürzung für die englische Bezeichnung 'script i' folgt.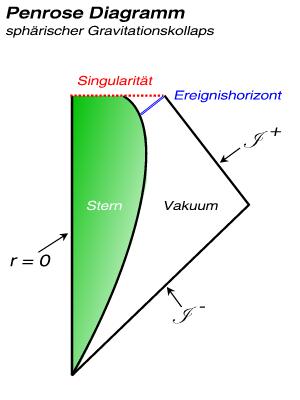

Noch mehr Unendlichkeiten

• Die vergangene Nullunendlichkeit ist ein Gebiet, wo die Differenz t – r gegen negativ unendlich geht, aber die Summe t + r endlich bleibt. Von hier aus kommen Nullgeodäten. In der Symbolik wird dies mit einem großen Skript-I mit Index – (gesprochen 'skrai minus') gekennzeichnet.
• Die zukünftige Nullunendlichkeit ist ein Gebiet, wo die Summe t + r gegen positiv unendlich geht, aber die Differenz t – r endlich bleibt. In diese Gebiete erstrecken sich auslaufende Nullgeodäten. In der Symbolik wird dies mit einem großen Skript-I mit Index + (gesprochen 'skrai plus') gekennzeichnet.

Transformation mit Tangens

Die konforme Transformation wird häufig mit der trigonometrischen Tangensfunktion umgesetzt. Der Tangens bildet endliche auf unendliche Intervalle ab, seine Umkehrfunktion macht entsprechend die inverse Transformation.

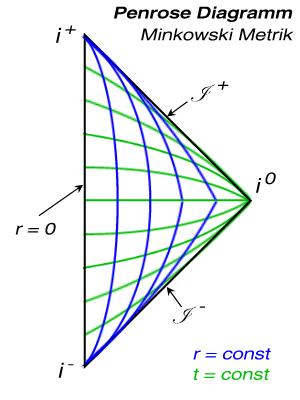
Beispiel 1: Minkowski-Metrik

Ein einfaches Beispiel für ein Penrose-Diagramm ist die flache Minkowski-Metrik der Speziellen Relativitätstheorie (Abbildung ganz am Anfang dieses Eintrags, zwei Dimensionen wurden unterdrückt!). Man kann das Minkowski-Linienelement sowohl in kartesischen, als auch in sphärischen Koordinaten ausdrücken. Auf der linken Kante, der Zeitachse, verschwindet die Radialkoordinate, r = 0. Man muss sich das Penrose-Diagramm um diese Achse rotiert vorstellen, um die beiden anderen, unterdrückten Dimensionen (φ, θ) zu erhalten. In der Abbildung sind außerdem Linien konstanten Radius und konstanter Zeit eingetragen. Die zeitartigen Geodäten verlaufen von unten, i^-, nach oben, i⁺. Die raumartige Unendlichkeit befindet sich rechts, i⁰. Radiale Nullgeodäten bilden einen Winkel von 45° mit der Vertikalen (einlaufend -45°, oben; auslaufend +45°, unten).

An dieser Winkelstellung von 45° kann man immer Nullgeodäten in Penrose-Diagrammen erkennen.

Beispiel 2: kollabierender Kugelstern

Ein weiteres Beispiel ist ein (idealisierter) sphärisch symmetrischer Gravitationskollaps eines massereichen Sterns zu einem stellaren Schwarzen Loch (siehe zweite Abbildung). Wiederum schließen die Nullgeodäten einen halben rechten Winkel mit der Vertikalen ein und markieren die Kanten der vergangenen (unten) und zukünftigen (oben) Nullunendlichkeit. Der Stern kollabiert und schrumpft immer mehr, bis sich der Ereignishorizont (blau) abschnürt. Er umschließt die intrinsische Singularität (rot), hier vom Schwarzschild-Typ. Das Gebiet zwischen roter und blauer Linie heißt eingefangene Fläche (engl. trapped surface).

Beispiel 3: Wurmloch

Das Penrose-Diagramm der Schwarzschild-Geometrie folgt durch Transformation auf Kruskal-Szekeres-Koordinaten. In diesem Diagramm (hier nicht gezeigt) erkennt man sehr gut die beiden Seiten des Wurmlochs, die durch die Einstein-Rosen-Brücke miteinander verbunden sind.