Die Petrov-Klassifikation ist ein Schema, um Raumzeiten nach unterschiedlichen Typen einzuordnen. Das Kriterium zur Klassifikation hängt mit einem bestimmten Tensor in der Allgemeinen Relativitätstheorie zusammen.

Präzise Definition

Diese Klassifikation basiert auf den Symmetrieeigenschaften des Weyl-Tensors. Die Theoretiker verwenden bei dieser Diskussion den so genannten Newman-Penrose-Tetraden-Formalismus, der fünf komplexe, skalare Größen, die Weyl-Skalare, liefert. Diese legen den Weyl-Tensor eindeutig fest. Die Weyl-Skalare sind wiederum Wurzeln der Petrov-Gleichung. Je nachdem, welche verschwinden, legt dies den Petrov-Typ fest. Die Relativitätstheoretiker unterscheiden

Typ I, II, D, III und N.

Dreieckshierarchie der Petrov-Typen

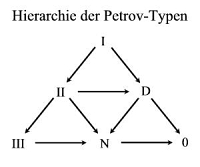Roger Penrose schlug eine Dreieckshierarchie der Petrov-Typen vor, die die Raumzeiten in ihren Spezialisierungen unterscheidet (siehe Abbildung rechts): In der Spitze des Dreiecks ist die Spezialisierung minimal, unten rechts ist sie maximal. Beispiel: Alle ungeladenen Schwarzen Löcher sind Vakuum-Lösungen der Einsteinschen Feldgleichungen. Dabei sind alle Schwarzen Löcher unabhängig davon, ob elektrisch geladen oder neutral, Petrov-Typ D.

Ordnung im Zoo der Raumzeiten

Ähnliche Schemata existieren für andere Nicht-Vakuum-Raumzeiten, die Plebanski-Typologie und Karlhede-Klassifikation heißen. Ziel dieser Klassifikationen ist eine Systematisierung der Raumzeiten der Allgemeinen Relativitätstheorie, um den Lösungsraum der Einsteinschen Feldgleichungen übersichtlicher zu machen und eventuell tiefere Einsichten in die Gravitationsphysik und Geometrie zu bekommen.