Der Riemann-Tensor oder Riemann-Christoffel-Tensor ist einer der wichtigsten Tensoren in Albert Einsteins Allgemeiner Relativitätstheorie (ART). Die alternative Bezeichnung Krümmungstensor offenbart seine physikalische Interpretation: er ist ein Maß für die Krümmung der Raumzeit.

Krümmung der Raumzeit

Die Krümmung verändert sich im Allgemeinen in der Raumzeit von Raumzeitpunkt zu Raumzeitpunkt. Die Physiker nennen das eine gekrümmte Raumzeit. Anschaulich mag man sich diese Raumzeit vorstellen, wie ein Gebirge mit Bergen und Tälern. Die Krümmungen werden – und das ist die Kernaussage der ART – durch eine Form von Energie, z.B. Masse, hervorgerufen. Die Information über die Energieform steckt in einem zweiten wichtigen Tensor der ART, dem Energie-Impuls-Tensor. Objekte, Testmassen oder auch Licht, die sich nun durch die gekrümmte Raumzeit (kräftefrei) bewegen, bleibt nichts anderes übrig, als den Krümmungen zu folgen. Die sich ergebenden, gewundenen Wege heißen Geodäten. Der gerade beschriebene Sachverhalt wird mathematisch mit den Einsteinschen Feldgleichungen ausgedrückt. Diese Gleichungen koppeln Energie-Impuls-Tensor und Riemann-Tensor. Prosaisch formuliert besagt dieser Satz gekoppelter, nichtlinearer, partieller Differentialgleichungen:

Masse und Energie sagen der Raumzeit wie sie sich zu krümmen hat, und die Raumzeit sagt der Energieform, wie sie sich zu bewegen hat.

Der Krümmungstensor – der komplizierteste Tensor der ART

Dringt man tiefer in die Tensorrechnung der ART ein, so stellt man fest dass der Riemannsche Krümmungstensor ein Tensor 4. Stufe ist. Diese Gebilde sind recht komplex und nicht leicht in der Handhabung: Denn der Krümmungstensor der ART hat 4⁴ = 256 Komponenten! Zum Glück weist der Riemann-Tensor einige Symmetrien auf, so dass er in den vier Dimensionen der klassischen ART (Länge, Breite, Höhe, Zeit) 20 voneinander unabhängige Komponenten hat.

Definition

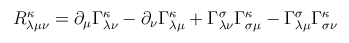Wie die Gleichung rechts zeigt, besteht der Riemann-Tensor R aus partiellen Ableitungen der Christoffel-Symbole ('Gammas, Γ, auch Levi-Civita-Zusammenhänge genannt). Diese wiederum sind partielle Ableitungen der Metrik. Im Krümmungstensor stecken demnach zweite Ableitungen der Metrik g_μν, oder man könnte auch sagen zweite Ableitungen der Mannigfaltigkeit. Auf diese Weise ist der Riemann-Tensor ein Maß für Krümmungen.

Teamarbeit von Einstein & Grossmann

Albert Einstein entdeckte die physikalische Relevanz des Krümmungstensors für seine Gravitationstheorie. Er griff dabei die Arbeiten des Mathematikers Georg Friedrich Bernhard Riemann (1826 – 1866) auf, der die fundamentalen Arbeiten seines Doktorvaters Carl Friedrich Gauß (1777 – 1855) weiterentwickelte. Der Mathematiker und Kommilitone Einsteins, Marcel Grossmann, gab den entscheidenden Hinweis auf die damals neuen Aspekte der Riemannschen Differentialgeometrie. Berühmt wurde die Bemerkung in Einsteins Züricher Notizbuch 'Grossmann Tensor vierter Mannigfaltigkeit', wo Einstein 1912 den Riemannschen Krümmungstensor identifizierte.

flach: R = 0

Verschwindet der Riemann-Tensor, so heißt die Metrik flach und weist daher keine Krümmungen auf.

Symmetrien des Riemann-Tensors

Der Riemann-Tensor besitzt eine Reihe von Symmetrien unter Vertauschung seiner vier Indizes, die teilweise auf die Symmetrie des metrischen Zusammenhangs (also der Christoffel-Symbole) zurückgehen. Daneben gibt es noch eine Reihe von Differentialidentitäten, die so genannten Bianchi-Identitäten, die der Riemann-Tensor erfüllt. Die Gültigkeit und Existenz von Bianchi-Identitäten ist tief verwurzelt in der Natur der Gravitation. Eine unglaublich interessante Diskussion, die diesen Sachverhalt beleuchtet, findet sich unter dem Eintrag Bianchi-Identitäten.

Verjüngungen des Riemann-Tensors und Invarianten

Die Verjüngungen des Riemann-Tensors heißen Ricci-Tensor und Ricci-Skalar (oder skalare Krümmung). Die innere Krümmung kann man als Skalar berechnen, indem man den Riemann-Tensor mit sich selbst kontrahiert, also ein Produkt bildet von kovarianten und kontravarianten Riemann-Tensor 4. Stufe. Dieses Produkt heißt Riemannsche Invariante (engl. Riemann invariant, Riemannian invariant, auch Kretschmann scalar, dt. Kretschmann-Skalar). Sie hat die nützliche Eigenschaft, dass sie unabhängig (invariant) vom zur Berechnung gewählten Koordinatensystem ist! Es ist also egal, welche Koordinaten man zur Berechnung auswählt: die Invariante hat immer denselben Wert.

Wo sind Krümmungssingularitäten?

Die Riemannsche Invariante einer Raumzeit eignet sich zum Auffinden ihrer echten, nicht behebbaren Singularitäten. Denn dort, wo die Riemannsche Invariante nicht definiert ist, wo 'durch eine Null geteilt wird', liegt eine unendliche Krümmung vor. Die Relativisten bezeichnen das als Krümmungssingularität. Dort versagt eine physikalische Beschreibung. Es zeichnet sich aktuell ab, dass eine Quantengravitation wie die Loop-Quantengravitation (Quantengeometrie) das Auftreten dieser Unendlichkeiten zu beheben vermag. Eine Quantisierung der Raumzeit scheint Krümmungssingularitäten zu verhindern!
Doch bleiben wir bei der klassischen, unquantisierten ART: Als Beispiel zum Auffinden von Singularitäten kann man die Raumzeit einer Punktmasse betrachten. Sie wird durch die Schwarzschild-Lösung beschrieben. Nicht rotierende, elektrisch ungeladene Schwarze Löcher werden im Rahmen der ART auch durch die Schwarzschild-Lösung repräsentiert. Möchte man sich die Riemannsche Invariante der Schwarzschild-Metrik beschaffen, muss man die metrischen Koeffizienten, die Komponenten des metrischen Tensors, ableiten. Daraus folgen in einem ersten Schritt die Christoffel-Symbole. Gemäß der Gleichung oben folgen aus den berechneten Christoffel-Symbolen die Komponenten des Riemann-Tensors. Die Rechenarbeit ist im Falle der Schwarzschild-Lösung noch gut zu bewältigen, weil sie eine hohe Symmetrie (Kugelsymmetrie) aufweist. Hat man sich einen Riemann-Tensor beschafft, so folgt der entsprechend dazu duale Tensor durch 'Überschieben' des metrischen Tensors (Kontraktion). Schließlich liegt der Riemann-Tensor in kontra- und kovarianter Form vor und kann miteinander multipliziert werden, um die Riemannsche Invariante zu erhalten.

Die echte Schwarzschild-Singularität

Die Riemannsche Invariante der Schwarzschild-Geometrie hat den Wert 48M²/r⁶, wobei M die Masse der Punktmasse oder auch des Schwarzen Loches ist. Diese Größe divergiert im Ursprung bei r = 0, so dass hier die echte Singularität der Schwarzschild-Lösung ist. Es handelt sich um eine Punktsingularität. Im Unendlichen, bei sehr großen Werten von r, verschwindet die Riemannsche Invariante, d.h. die Krümmung geht gegen null und die Raumzeit wird asymptotisch flach.

Die echte Kerr-Singularität

Die gleiche Rechenprozedur kann man für eine weniger symmetrische Raumzeit durchführen, z.B. für rotierende Schwarze Löcher, die durch die Kerr-Lösung dargestellt werden. Hier liegt eine Axialsymmetrie vor, die die Berechnung der Riemannschen Invarianten zu einem deutlich längeren Unterfangen macht. Die Riemannsche Invariante der Kerr-Geometrie ist entsprechend komplizierter und lautet (Glass & Krisch, Class. Quantum Grav. 21, 5543, 2004):

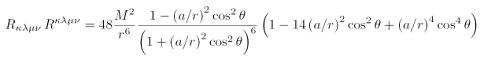
Wie man sofort sieht, geht diese Invariante für a=0 in die der Schwarzschild-Lösung über. Um das Wesen der echten Singularität der Kerr-Lösung herauszufinden, ist nun zu diskutieren, wann der Nenner der Riemannschen Invarianten verschwindet. Denn der Grenzwert von etwas Konstantem durch null geht gegen unendlich und markiert die Krümmungssingularität. Umschreiben liefert eine Bedingung, die besagt, dass die Boyer-Lindquist-Funktion ρ verschwinden muss. Das ist gegeben, wenn gleichzeitig die Bedingungen r = 0 und θ = π/2 (bzw. 90°) erfüllt sind. Besser ist dieses Ergebnis mit Kerrs ursprünglichem, kartesischen Koordinatensystem zu interpretieren: Es liefert x² + y² = a² und z = 0, also eine Ringsingularität, die genau in der Äquatorialebene liegt.

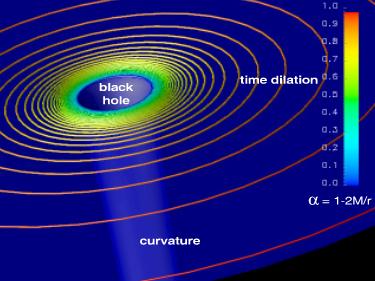
Gravitationstrichter

In der Abbildung oben ist die gekrümmte Schwarzschild-Geometrie auf einem Computer visualisiert worden sind (Müller 2005). Das Bild enthält zweierlei Informationen: die Krümmung der Raumzeit (blaue 'Gummihaut') und die gravitativ bedingte Zeitdilatation (farbige Isokonturlinien). Es handelt sich also um einen so genannten Gravitationstrichter. Der tiefe blaue Schlund im Zentrum besagt gerade, dass die Krümmung im Zentrum des Loches unendlich wird. Der Schlund schließt sich unten nicht! Das markiert den Ort der zentralen Punktsingularität. Die Uhren ticken aus der Sicht eines Außenbeobachters immer langsamer und bleiben schließlich am Ereignishorizont (hier identisch mit dem Schwarzschild-Radius, der innerste blaue Ring) stehen. Die Farbskala am Bildrand zeigt den Wertebereich der Lapse-Funktion (auch Rotverschiebungsfaktor genannt), die zwischen 1 (asymptotisch flache Raumzeit) und 0 (stark gekrümmte Raumzeit am Horizont) variiert. Ein einfallendes Objekt würde also immer langsamer werden und bei Erreichen des Horizonts (von außen gesehen) stehen bleiben. Das Abstoppen ist allerdings nicht mehr sichtbar, weil jede Strahlung unendlich stark rotverschoben wird, die vom Horizont kommt. Die Ursache dafür ist die Gravitationsrotverschiebung. Es sei angemerkt, dass aus der Sicht des einfallenden Objekts, die zentrale Punktsingularität in endlicher Zeit erreicht wird. Das ist eben der gewichtige Unterschied der Bezugssysteme und das Wesen der Relativitätstheorie.
Es sei auch darauf hingewiesen, dass es sich bei dem Bild nicht um eine Visualisierung handelt, die einem realen Foto eines Schwarzen Loches gleichkommt – es ist nur eine Darstellung mathematischer Größen in Falschfarben. Einem echten Foto kommt die relativistische Ray-Tracing-Simulation einer leuchtenden Gasscheibe um ein Loch im Eintrag Schwarzes Loch nahe, das ebenfalls als Falschfarbenbild dargestellt wird.