Die Thermodynamik (auch Wärmelehre) ist eine sehr alte, klassische Disziplin der Physik, die phänomenologisch makroskopische Größen, wie Temperatur, Dichte, Druck, Entropie etc. zueinander in Beziehung setzt.
Im Rahmen der statistischen Physik ist eine Verbindung des Mikrokosmos und des Makrokosmos möglich, indem man statistische Ensembles von Teilchen betrachtet und die Gesetze der Quantenstatistik berücksichtigt. Das Spin-Statistik-Theorem fordert eine fundamentale Unterscheidung von Teilchen in Bosonen und Fermionen. Wichtige Anwendungen sind Zustandsgleichungen von Gasen wie die Quantengase (Bosegas und Fermigas) oder auch Bose-Einstein-Kondensation und Supraleitung.

Thermodynamik Schwarzer Löcher

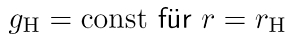Wichtig im Zusammenhang mit Schwarzen Löchern wird die Thermodynamik, weil sich eine analoge Behandlung zu den thermodynamischen Hauptsätzen herausgestellt hat, wenn man entsprechende Größen der Theorie Schwarzer Löcher mit den klassischen thermodynamischen Größen identifiziert. Diese Analoga haben Bardeen, Carter & Hawking 1973 gefunden. Eine wesentliche Größe, die man studieren kann, ist die Fläche des Ereignishorizontes, die mit der Masse des Schwarzen Loches ansteigt und mit der Rotation des Loches abfällt. Eine bemerkenswerte Eigenschaft ist, dass, wenn zwei Schwarze Löcher verschmelzen, die Fläche des neuen Horizontes größer ist, als die Summe der Flächeninhalte der einzelnen, kollidierenden Schwarzen Löcher, ähnlich der Dreiecksungleichung aus der Geometrie. Dieses Phänomen kann man mit dem Konzept der Entropie aus der Thermodynamik in Verbindung bringen: Nach dem Zweiten Hauptsatz der Thermodynamik steigt die Entropie (Maß für Unordnung in einem System, fehlende Information) immer an! Genauso verhält es sich mit der Fläche des Horizontes: die Bekenstein-Hawking-Entropie ist proportional zur Fläche des Horizontes und hängt sonst nur von Naturkonstanten ab!
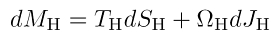Das Analogon zur thermodynamischen Temperatur ist die so genannte Oberflächengravitation, eine Größe, die ein Maß für die Stärke des Gravitationsfeldes am Horizont ist. Ein FIDO würde in der Nähe des Loches eine divergierende Kraft messen. Renormiert man diese Kraft, so erhält man die Oberflächengravitation. Eine kurze Rechnung zeigt, dass Oberflächengravitation und Rotation konstant auf dem Horizont sind, d.h. unabhängig vom Polarwinkel. Dies ist der Nullte Hauptsatz. Die Formulierung des Ersten Hauptsatzes gewinnt man, indem man die intensiven Zustandsgrößen Oberflächengravitation und 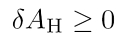Rotation mit den entsprechenden extensiven Größen Oberfläche und Drehimpuls verknüpft, die schließlich die Gesamtenergie des Systems, also die Masse des Schwarzen Loches liefern. Das Analogon zum klassischen Temperaturbegriff heißt in der Theorie Schwarzer Löcher Hawking-Temperatur.
Schließlich lautet das Pendant zum Dritten Hauptsatz, die Unerreichbarkeit des absoluten Nullpunkts (bei exakt null Kelvin), dass bei Schwarzen Löchern die Oberflächengravitation nie Null werden kann.
Die thermische Strahlung von Schwarzen Körpern besitzt ihr Pendant in der Hawking-Strahlung. Hawking konnte 1974 zeigen, dass die Oberflächengravitation der thermodynamischen Temperatur entspricht und eine ähnliche Formulierung wie für Plancksche Strahler möglich ist.

Bedeutung für die Astrophysik

Wenn auch viele Aspekte dieser Betrachtung sehr theoretisch anmuten, so besitzt sie dennoch eine unmittelbare Relevanz für die Astronomie: Schwarze Löcher verfügen neben er Akkretionsenergie über einen zweiten Energiekanal: Etwa 30% der Gesamtenergie stecken in der Rotation! Ein Abbau dieser Rotationsenergie (ähnlich wie bei Pulsaren) liefert nochmals eine vergleichbare Leuchtkraft wie die Akkretionsleistung. Für Aktive Galaktische Kerne (AGN), die im Innern ein supermassereiches Schwarzes Loch beherbergen, bedeutet dies, dass eine Zweiteilung vorliegen sollte: die eine Klasse gewinnt Energie aus der Akkretion (radio-leise Objekte), die andere gewinnt auch Energie aus der Rotation (radio-laute Objekte), die in Jets umgewandelt wird! Die Beobachtung kann diese These stützen.

Literatur

• Bardeen, J.M., Carter, B. & Hawking, S.W.: The Four Laws of Black Holes Mechanics, Commun. Math. Phys. 31, 161, 1973