Atommodell, Vorstellung (Bild) von der Struktur und dem Aufbau eines Atoms, die im Laufe der Zeit aus den Ergebnissen experimenteller Untersuchungen gewonnen wurde. Zunächst betrachtete man das Atom als starre, homogene Kugel. Insbesondere die Streuversuche von Lenard und Rutherford mit Elektronen bzw. α-Teilchen (Radioaktivität) an dünnen Metallfolien zeigten, daß das Atom eine Struktur besitzt. Außerdem erkannte man, daß Atome entgegen dem Wortsinn nicht unteilbar sind. Folgende A. wurden entwickelt:

Das Rutherfordsche A. Nach den theoretischen Betrachtungen der Streuversuche besteht ein Atom aus einem sehr kleinen Kern mit einem Radius von etwa r_K = 10^-14 m, der Z positive Elementarladungen enthält und der nahezu die gesamte Masse in sich vereint, sowie der negativ geladenen Elektronenhülle. Aufgrund der Neutralität des Atoms entspricht die Anzahl der Elektronen in der Hülle der Kernladungszahl Z, die gleichzeitig die Ordnungszahl des Elements im Periodensystem bestimmt. Um den ständigen Aufenthalt der Elektronen in unmittelbarer Kernnähe erklären zu können, wurde ein dynamisches Modell eingeführt, wonach die Elektronen auf Kreis- bzw. elliptischen Bahnen den Atomkern ähnlich wie Planeten die Sonne umkreisen (Planetenmodell). Die Zentrifugalkraft wird durch die elektrostatische Kernanziehung kompensiert. Nach den verschiedenen Bestimmungsmethoden sind die Atomradien von der Größenordnung 10^-10 m. Das Rutherfordsche A. steht jedoch im Widerspruch zu den Gesetzen der klassischen Elektrodynamik und kann die experimentellen Befunde der Atomspektroskopie nicht erklären. Danach wären die Atome instabile Gebilde, die während ihrer Existenz Licht in Form eines kontinuierlichen Spektrums aussenden. In Wirklichkeit sind Atome mit Ausnahme der radioaktiven Kerne stabil. Erst durch Energiezufuhr senden sie Strahlen als charakteristische Linienspektren aus.

Das Bohrsche A. Dieses baut unmittelbar auf den Vorstellungen des Rutherfordschen A. auf. Zur Überwindung des Stabilitätsproblems führte Bohr Postulate ein. Die Bohrschen Postulate sind Forderungen, die nicht aus der klassischen Physik folgen und teilweise im Widerspruch zu ihr stehen. Danach kann das Elektron den Atomkern nur auf ganz bestimmten Bahnen (erlaubte Bahnen) umkreisen, auf denen es im Gegensatz zu den Gesetzen der klassischen Physik keine elektromagnetische Strahlung emittiert. Auf diesen "strahlungsfreien" Bahnen, die als stationäre Zustände bezeichnet werden, hat das Elektron eine bestimmte Energie. Diese erlaubten Bahnen sind dadurch charakterisiert, daß bei ihnen der Betrag des Drehimpulses gleich einem ganzzahligen Vielfachen der Naturkonstante

= h/2π (h = Plancksches Wirkungsquantum) sein muß. Auf diese Weise erreichte Bohr die Quantisierung der Bahnradien r_n und der Energien E_n in Abhängigkeit der Quantenzahl n (n = 1, 2, 3, ...). Der kleinste Bahnradius (n = 1) für das Elektron im Wasserstoffatom wird als Bohrscher Atomradius r₁ ≡ a₀ = 1 Bohr = 52,9 pm bezeichnet. Er dient als Einheit der Länge im System atomarer Einheiten. Der Übergang eines Elektrons von einem stationären Zustand der Energie E_n in einen anderen der Energie E_m kann in Abhängigkeit vom Energieinhalt des Ausgangs- und Endzustandes durch Energieaufnahme bzw. -abgabe erfolgen, wobei die Energiedifferenz nach der Bohrschen Frequenzbedingung ΔE = E_n – E_m = hν als elektromagnetische Strahlung der Frequenz ν absorbiert bzw. emittiert wird. Mit Hilfe des Bohrschen A. gelang es erstmalig, das Linienspektrum für das Wasserstoffatom theoretisch zu deuten und wesentliche Züge des Periodensystems der Elemente zu klären.

Die Schwierigkeiten des Bohrschen A. konnten erst mit der Entwicklung einer neuen, allgemeineren Theorie, der Quantenmechanik, beseitigt werden, die in den zwanziger Jahren dieses Jahrhunderts im wesentlichen durch die Arbeiten von Schrödinger, Heisenberg, Born und de Broglie geschaffen wurde.

Das quantenmechanische A. Es stellt eine grundsätzliche Neufassung der Atomtheorie dar. Die Quantenmechanik fußt auf der Doppelnatur der Materie, wonach Licht, Elektronen und andere mikroskopische Objekte Teilchen- und Wellencharakter aufweisen können. Dies kommt in der de-Broglie-Beziehung λ =h/p zum Ausdruck, die die Wellenlänge λ und den Impuls p als Teilcheneigenschaft über das Plancksche Wirkungsquantum h verknüpft. Daraus resultiert ein Grundprinzip der neuen Theorie – die Heisenbergsche Unschärferelation. Sie besagt, daß gleichzeitige Aussagen über den Ort und den Impuls von Teilchen mit einer Unbestimmtheit behaftet sind.

Mathematisch wird die Unschärferelation durch die Beziehung ΔxΔp ≥ h ausgedrückt. Danach muß das Produkt aus der Unbestimmtheit des Ortes Δx und der des Impulses Δp mindestens von der Größenordnung des Planckschen Wirkungsquantums sein. Für Mikroobjekte, wie Elektronen und Nucleonen, kann daher keine Bahnkurve angegeben werden. Die Bohrsche Atomtheorie verletzt daher bereits im Ansatz das Unschärfeprinzip, indem sie den Elektronen eine Bahn und eine Geschwindigkeit zuordnet. Die Erfahrung hat gezeigt, daß für zeitunabhängige Vorgänge die Wahrscheinlichkeit ein Teilchen im Volumenelement dτ = dx dy dz am Ort P(x,y,z) anzutreffen, durch die Beziehung dW = Ψ*(x,y,z) Ψ(x,y,z) dτ = |Ψ|² dτ angegeben werden. Ψ(x,y,z) wird als Wellenfunktion des Teilchens bezeichnet. Das Betragsquadrat der Wellenfunktion |Ψ|² ist das Produkt aus der Wellenfunktion Ψ und der zu ihr konjugiert komplexen Funktion Ψ* und wird Wahrscheinlichkeitsdichte genannt. Neben der Wellenfunktion sind in der Quantenmechanik Operatoren  von fundamentaler Bedeutung, die eine mathematische Vorschrift darstellen. Es hat sich gezeigt, daß jeder physikalischen Meßgröße ein Operator zugeordnet werden kann, dessen Wirkung auf die Wellenfunktion die Meßwerte der Observablen in Form der Eigenwerte liefert. Dieser Zusammenhang wird durch die Beziehung ÂΨ_n = A_nΨ_n, die Eigenwertgleichung, ausgedrückt. Die Funktionen Ψ_n werden als Eigenfunktionen und die Zahlen A_n als Eigenwerte des Operators  bezeichnet. Die Eigenwertgleichung der Energie heißt nach ihrem Entdecker Schrödinger-Gleichung. Sie ist bei der Behandlung des quantenmechanischen A. von zentraler Bedeutung. Für ein Teilchen der Masse m hat sie in kartesischen Koordinaten die Form

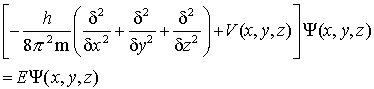
Atommodell. Abb.: 1 Winkelteile Y_reell(θ,φ). s, p, d ... bezeichnen Atomzustände mit der Quantenzahl l = 0, 1, 2, 3 ...

Der Ausdruck der eckigen Klammern wird als Hamilton-Operator

bezeichnet. Er enthält die klassische potentielle Energie V(x,y,z) des Teilchens sowie die partiellen Ableitungen 2. Ordnung nach den Variablen. Für das Wasserstoffatom kann die Schrödinger-Gleichung exakt gelöst werden, wenn man anstelle der kartesischen Koordinaten Polarkoordinaten (r,θ,φ) verwendet, da somit ein besonders einfacher Ausdruck für die potentielle Energie des Elektrons resultiert und die Separation der Variablen gelingt. Mit dem Produktansatz Ψ(r,θ,φ) = R(r)Θ(θ)Φ(φ) wird die Lösung der partiellen Differentialgleichung 2. Ordnung mit drei Variablen auf die Lösung von drei entsprechenden Differentialgleichungen mit je einer Variablen zurückgeführt. Aus dem mathematischen Charakter der Schrödinger-Gleichung und aus den physikalischen Randwertbedingungen folgt, daß Lösungen nur für bestimmte Wellenfunktionen Ψ_n (Eigenfunktionen) mit den zugehörigen Eigenwerten E_n für die Energie existieren. Die Ψ-Funktionen, die die stationären Zustände des Elektrons beschreiben, nennt man Orbitale. Bezieht man sich dabei auf Elektronen in einem Atom, so spricht man von Atomorbitalen (Abk. AO). Die Wellenfunktionen, d. h. die Atomorbitale Ψ_n,l,ml(r,θ,φ) hängen von den drei Variablen r, θ, φ ab und sind im Wasserstoffatom sowie bei Mehrelektronenatomen in der Näherung der unabhängigen Teilchen (Zentralfeldmodell, Elektronenkonfiguration) durch die drei Quantenzahlen n, l, m_l näher bestimmt. Die Quantenzahlen können nur ganz bestimmte Werte annehmen und stehen in folgendem Zusammenhang: n = 1, 2, 3 ..; l = 0, 1, 2 ..., n – 1; m_l = -l, -l + 1 ..., – 1, 0, + 1 ..., l, wobei n die Hauptquantenzahl, l die Bahndrehimpulsquantenzahl und m_l die Magnetquantenzahl bedeuten. Dabei charakterisieren l den Betrag des Bahndrehimpulses L_l und m_l die Komponente von L_l in z-Richtung. Atomorbitale gleicher Hauptquantenzahlen werden zu einer Schale zusammengefaßt. Für n = 1, 2, 3 ... sind die Buchstabenbezeichnungen K, L, M ... gebräuchlich. Atomorbitale mit gleicher Haupt- und Bahndrehimpulsquantenzahl werden mit dem Begriff Unterschale bezeichnet. Es ist üblich, Atomorbitale entsprechend ihren l-Werten mit Buchstaben zu kennzeichnen, die auf alte Termbezeichnungen aus der Spektroskopie zurückgehen. Für l = 0, 1, 2, 3 setzt man s, p, d, f.

Die Symbolisierung der Atomorbitale erfolgt in der Weise, daß n als Ziffer geschrieben wird und für l die obige Buchstabenbezeichnung verwendet wird. So entspricht z. B. ein Zustand mit n = 3 und l = 1 einem 3p-Atomorbital. Im Wasserstoffatom hängen die Energiewerte E_n des Elektrons nur von der Hauptquantenzahl ab. Da zu jedem Wert von n insgesamt n² Zustände derselben Energie gehören, ist im Wasserstoffatom jedes Energieniveau n²-fach entartet. So haben z. B. das 2s- und die 2p-Orbitale den gleichen Energiewert. Die Darstellung der Atomorbitale Ψ_n,l,ml(r,θ,φ) des Wasserstoffatoms und besonders die ihres Betragsquadrates |Ψ|², die die Verteilung der Elektronendichte um den Atomkern veranschaulicht, ist für qualitative Betrachtungen der chemischen Bindung von großer Bedeutung. Man muß sich aber bei der Veranschaulichung auf Teildarstellungen beschränken. Dafür ist es zweckmäßig, Ψ_n,l,ml(r,θ,φ) als Produkt aus einem Radialteil R_n,l(r) und einem Winkelteil Y_l,ml(θ,φ) zu schreiben. Die auf eins normierten Funktionen Y_l,ml(θ,φ) bezeichnet man als Kugelfunktionen. Durch geeignete Linearkombinationen der komplexen Winkelteile können reelle Winkelteile Y_reell(θ,φ) erhalten werden. Sie haben gegenüber den komplexen Formen den Vorteil, daß ihre Richtungsabhängigkeit unmittelbar aus den analytischen Ausdrücken hervorgeht. Die Y_reell(θ,φ) stellen Flächen im Raum dar und werden meist als Schnitt mit der xz- bzw. yz-Ebene dargestellt. In Abhängigkeit von l und m_l ergeben sich unterschiedliche Formen und Vorzugsrichtungen (Abb. 1). Die Vorzeichen der Winkelteile haben keine physikalische Bedeutung. Sie sind nützlich für die Betrachtung der Symmetrieeigenschaften von Orbitalen bezüglich der Elektronenstruktur von Molekülen. Die Quadrate der Winkelteile Y²_reell(θ,φ), die in ihrer Form den Y_reell(θ,φ) sehr ähnlich sind, veranschaulichen die Verteilung der relativen Elektronendichte auf einer Kugeloberfläche mit einem konstanten Radius r. Es resultieren allgemein l Knotenflächen (Y²_reell = 0), in denen die Aufenthaltswahrscheinlichkeit des Elektrons Null beträgt. Die größte Anschaulichkeit hat die Größe 4πr²R²_n,l(r), die als Radialverteilung bezeichnet wird. Sie bestimmt die Aufenthaltswahrscheinlichkeit des Elektrons in einer Kugelschale mit dem Radius r und der Dicke dr. Das Maximum der Aufenthaltswahrscheinlichkeit für ein Elektron im 1s-Orbital des Wasserstoffatoms wird im Abstand des Bohrschen Radius a₀ erhalten (Abb. 2). Im Gegensatz zum Bohrschen A. hat das Elektron jedoch bei anderen Abständen ebenfalls eine von Null verschiedene Aufenthaltswahrscheinlichkeit. Mit zunehmendem n sind die Maxima der Radialverteilung nach größeren Werten von r verschoben. Es resultieren n – l – 1 radiale Knotenflächen zwischen 0 < r < ∞. Die Teildarstellungen der Quadrate der Winkel- und Radialteile können jeweils nur ein unvollständiges Bild über die Verteilung der Elektronendichte im Raum vermitteln. Wie die Beobachtung zeigt, ist zur eindeutigen Charakterisierung eines Elektrons in einem Atom eine weitere Quantenzahl, die Spinquantenzahl m_s (Elektronenspin), erforderlich. Sie beschreibt den Eigendrehimpuls des Elektrons und kann die Werte m_s = ±1/2 annehmen. Die gewonnenen Erkenntnisse und Vorstellungen über die Elektronenstruktur des Wasserstoffatoms werden bei der näherungsweisen Behandlung von Mehrelektronenatomen genutzt (Zentralfeldmodell). Der Vorzug des quantenmechanischen A. besteht in seiner theoretischen Geschlossenheit und der sehr guten Übereinstimmung seiner Aussagen mit experimentellen Befunden.

Atommodell. Abb. 2: Radialverteilung für ein Elektron im Wasserstoffatom.