Maxwell-Boltzmann-Verteilung, Gesetzmäßigkeit für die Teilchengeschwindigkeiten in einem Gas, das sich im thermischen Gleichgewicht befindet.

Ein Gas enthält eine sehr große Anzahl von Teilchen (im Normzustand 2,69·10²² dm^-3), die sich in regelloser Bewegung befinden. Zwischen den Molekülen finden ständig Zusammenstöße statt, bei denen sich Richtung und Betrag der Teilchengeschwindigkeit verändern. Es stellt sich eine Geschwindigkeitsverteilung ein, welche sich durch eine Verteilungsfunktion beschreiben läßt, die man wegen der hohen Teilchenzahlen mathematisch als kontinuierliche Funktion formulieren kann.

Unter der Voraussetzung, daß die Moleküle keine inneren Freiheitsgrade haben und die klassische Mechanik gilt (nicht gequantelter Energieaustausch, Energie- und Impulserhaltungssatz), läßt sich auf verschiedenen Wegen die M. begründen:

dNν/N = (2/π)^1/2(m/kT)^3/2e^-mν2/2kTν² dν = f(ν) dν.

Hierbei bedeuten k Boltzmann-Konstante, T absolute Temperatur, m Teilchenmasse, ν Betrag der Teilchengeschwindigkeit und N Gesamtzahl der Teilchen im Gas. dNν gibt die Anzahl der Teilchen an, deren Geschwindigkeit in dem differentiellen Geschwindigkeitsintervall zwischen ν und ν + dν liegt. Damit ist der Quotient dNν/N der Bruchteil aller Teilchen, der innerhalb dieses Intervalls liegt, oder die Wahrscheinlichkeit für das Auftreten dieser Geschwindigkeit.

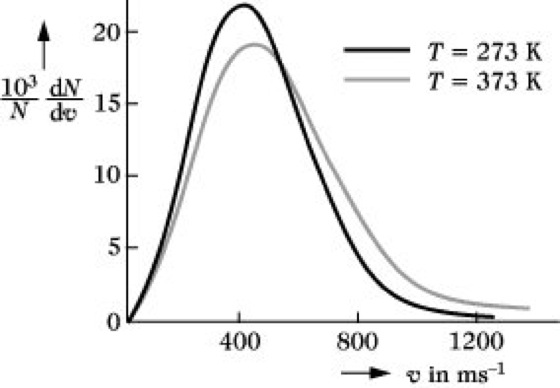
Maxwell-Boltzmann-Verteilung. Abb.: Geschwindigkeitsverteilung von Sauerstoff.

Die Abb. zeigt, daß der größte Anteil der Moleküle Geschwindigkeiten in der Nähe der wahrscheinlichsten Geschwindigkeit ν_w, d. h. des Maximums, hat. Aus df(ν)/dν = 0 folgt

. Da die Kurve

nicht symmetrisch ist, entspricht ν_w nicht der mittleren Geschwindigkeit ν^-, sondern die letztere ist etwas größer.

Durch Mittelwertbildung

erhält man

Eine dritte wichtige Größe ist das mittlere Geschwindigkeitsquadrat ν^-2-= 3kT/m = 3ν²_w/2. Sowohl ν_w als auch ν^- erhöhen sich mit der Temperatur um den Faktor

, d. h., die Geschwindigkeitsverteilung verschiebt sich zu höheren Geschwindigkeiten. Gleichzeitig wird die Verteilung breiter und flacher (Abb.).

Eine grundlegende Annahme der Statistik (Thermodynamik III) besagt, daß für eine physikalische Größe der Mittelwert über eine sehr große Menge von Teilchen zu einem bestimmten Zeitpunkt (Scharmittel) gleich dem Mittelwert für ein Einzelobjekt über einen sehr langen Zeitraum (Zeitmittel) ist. Damit läßt sich die M. auch als eine Wahrscheinlichkeitsverteilung der Geschwindigkeiten auffassen, die ein einzelnes Molekül über einen langen Beobachtungszeitraum in dem Gas annimmt. Es ändert durch Stöße laufend seine Geschwindigkeit und hat im zeitlichen Mittel die Geschwindigkeit ν^- und das mittlere Geschwindigkeitsquadrat ν^-2-. Seine mittlere kinetische Energie E = m ν^-2-/2 beträgt folglich E = ³/₂kT. Daraus folgt für die molare Wärmekapazität der hier betrachteten Gase C_v = ³/₂R oder der Anteil ¹/₂R je Translationsfreiheitsgrad.

Substituiert man in der M. die Geschwindigkeit v durch die kinetische Energie ε = mν²/2 oder

ergibt sich die Energieverteilung dNε/N = 2π^-1/2(kT)^-3/2ε^1/2e-ε/kT dε im Gleichgewichtszustand.

Die M. läßt sich experimentell mit Hilfe von Atom- oder Molekularstrahlen direkt nachweisen. Dabei werden die Teilchen nach ihren verschiedenen Flugzeiten mit Hilfe eines rotierenden Zylinders (Stern 1920) oder auch nach dem Fizeau-Prinzip (Lammert 1929) aufgelöst.