van-der-Waalssche Gleichung, eine Zustandsgleichung, die das thermische Verhalten sowohl von realen Gasen als auch von Flüssigkeiten näherungsweise beschreibt. Sie lautet für 1 mol (p + a/V²) (V - b) = RT, wobei p den Druck, V das Molvolumen, T die absolute Temperatur und R die Gaskonstante bezeichnen, a und b sind stoffspezifische Konstanten. Im Unterschied zur thermischen Zustandsgleichung idealer Gase enthält die v. G. zwei Korrekturglieder, den Kohäsions- oder Binnendruck a/V² und das Covolumen b. Der Kohäsionsdruck wird durch Anziehungskräfte zwischen den Teilchen verursacht, die wie eine Druckerhöhung wirken.

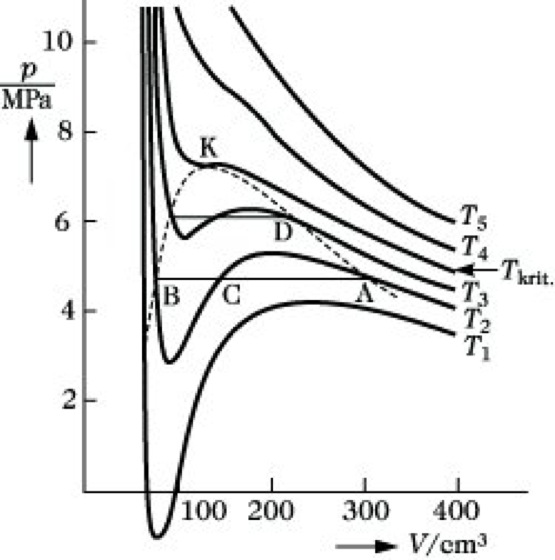
Van-der-Waalsche Gleichung. Abb.: p,V-Diagramm des Kohlendioxids.

Das Covolumen kann als Maß für das Eigenvolumen aller Teilchen, aus denen das Gas besteht, aufgefaßt werden. Mit steigendem Druck gewinnt es immer mehr an Bedeutung und verringert die Kompressibilität des realen Gases im Vergleich zum idealen Gas.

Die v. G. ist eine Gleichung dritten Grades bezüglich V, d. h., bei einer vorgegebenen Temperatur liefert sie für einen Druck als Lösungen drei verschiedene Volumina (Abb.). Oberhalb der Isothermen T_krit sind zwei dieser Lösungen komplex, haben also physikalisch keine Bedeutung. Jedem Druck p entspricht ein bestimmtes Volumen V.

Unterhalb T_krit beschreibt die v. G. die Existenz eines Zweiphasengebietes. Wird das Gas z. B. isotherm bei der Temperatur T₂ komprimiert, so steigt der Druck. Am Punkt A beginnt das Gas zu kondensieren. Der Druck bleibt konstant, bis am Punkt B das gesamte Gas in den flüssigen Zustand übergeführt worden ist. Weitere Volumenverringerung führt zu einem sehr steilen Anstieg der Isothermen, da die Kompressibilität der Flüssigkeit viel geringer als die des Gases ist. Der Punkt A entspricht folglich dem Molvolumen des gesättigten Dampfes, B dem Molvolumen der Flüssigkeit am Siedepunkt T₂. Die dem Punkt C entsprechende Lösung ist physikalisch nicht sinnvoll. Mit steigender Temperatur wird das Zweiphasengebiet schmaler und verschwindet an der Isotherme T_krit, die nur noch einen Wendepunkt aufweist. Der Punkt K entspricht dem kritischen Punkt. Oberhalb der kritischen Temperatur T_krit ist das Gas nicht mehr verflüssigbar. Die kritischen Daten können aus der Lage des Wendepunktes berechnet werden. Aus dp/dV = 0 und d²p/dT² = 0 folgt: V_krit = 3b, p_krit = a/27b² und T_krit = 8a/27bR. Führt man unter Nutzung dieser kritischen Daten die reduzierten Größen V_r = V/V_krit, p_r=p/p_krit und T_r = T/T_krit in die v. G. ein, so erhält sie die Form (p_r + 3/V_r²) (3 V_r – 1) = 8 T_r. Diese Gleichung enthält keine stoffspezifischen Konstanten mehr und stellt eine spezielle Form des Theorems der übereinstimmenden Zustände dar.