Lexikon der Geographie: ökologische Modellbildung
ökologische Modellbildung, Bildung von Modellen im Bereich der Ökologie. Die erste Stufe ist der Entwurf eines konzeptuellen Modells, das die Struktur des Systems durch Einführung von Kompartimenten und Flüssen abstrahiert ( Abb. 1). Kompartimentmodelle für Masse- und Energieflüsse basieren auf dem Konzept der trophischen Ebenen. Eine trophische Ebene fasst Organismen bezüglich ihrer Position in der Hierarchie der Nahrungskette zusammen. Die Kompartimente eines Minimalökosystems umfassen Primärproduzenten, Herbivoren, Karnivoren, Destruenten und Nährstoffe. Dieses Modell ist hochgradig aggregiert. Die Zustandsvariablen sind die Biomassen der Kompartimente. Es gelten die Bezeichnungen: yi=Biomasse oder Energiegehalt der trophischen Ebene i, Fi=Massefluss (oder Energiefluss) vom i-ten zum j-ten Kompartiment (Index 0 bezieht sich auf die Umwelt), n=Anzahl der Kompartimente.
Der erste Schritt des Entwurfs eines mathematischen Modells besteht in der Aufstellung von Massenbilanzgleichungen. Diese haben die Form: 
i=1...n.
Dabei werden Flüsse in das Kompartiment mit positivem, aus dem Kompartiment heraus mit negativem Vorzeichen versehen. So bedeutet F12 den Fluss vom Kompartiment Primärproduzent in das Kompartiment Herbivor, F10 bedeutet den Fluss von den Primärproduzenten in die Umgebung, z.B. der CO2-Verlust durch Atmung. Die Massenbilanzgleichungen leiten sich unmittelbar aus der Strukturinformation ab. Schwieriger ist die Formulierung der Flüsse als Funktion der Zustandsvariablen. Diese können nur empirisch aus Experimenten abgeleitet werden. Für die Interaktion zwischen Primärproduzent und Herbivor wird häufig eine Sättigungsfunktion analog einer Michaelis-Menten-Enzymkinetik verwendet: 
Dabei hat der erste Faktor der zweiten Gleichung die Bedeutung der Konsumrate pro Herbivor in Abhängigkeit des Angebotes y1. Die Parameter sind leicht interpretierbar: Vmax ist die maximale Konsumrate bei Überflussangebot, Ks ist die Halbsättigungskonstante.
Die Abbildung 2 fasst einige häufig verwendete Ausdrücke für die Flüsse zusammen. Die meisten Interaktionsterme (die Flüsse) sind nichtlineare Funktionen der Zustandsvariablen. Das in der ersten Gleichung formulierte DGL-System, versehen mit Ansätzen für die Flüsse wie in der Abbildung 2, stellt somit eine vernetztes nichtlineares System dar. Je nach Art der Nichtlinearitäten kann ein solches System ein vielfältiges dynamisches Verhalten aufweisen. Es kann multiple stationäre Zustände besitzen, es können Grenzzyklen auftreten oder sogar "seltsame Attraktoren".
Dieses konzeptuelle Modell hat noch keinen räumlichen Bezug. Es ist daher notwendig, zu definieren, für welchen Bilanzierungsraum das Kompartimentsystem gelten soll. Dieser kann sein eine pedologische Einheit, d.h. eine bezüglich der Bodenparameter homogene Fläche, oder ein Ökotop, entstanden aus der Verschneidung von pedologischer Einheit mit der Landnutzung, aber auch die gesamte Biosphäre, wenn hochgradig aggregierte biogeochemische Stoffkreisläufe betrachtet werden. Die in der Abbildung 2 dargestellten Ansätze für die Flüsse können weiter detailliert werden, wenn die physiologischen Prozesse auf der Ebene der Biochemie modelliert werden. Für die Photosynthese eines Blattes ist das folgende Modell international anerkannt, welches die Prozesse der CO2-Bindung an das Enzym RUBISCO durch einen enzymkinetischen Ansatz beschreibt: 
wobei AC=Nettoprimärproduktion, Γ =Kompensationspunkt der Photorespiration, C=CO2-Konzentration, O=O2-Konzentration, WC=Geschwindigkeit der durch die RUBISCO katalysierten CO2-Bindung bei Lichtsättigung, WJ=Geschwindigkeit der CO2-Bindung bei Begrenzung der Reaktion durch die photochemischen Prozesse, Rd=Dunkelatmung, I=Strahlung im photosynthetisch aktiven Bereich des Spektrums [mol Quanten/m2/s], Kc, Ko=Bindungskonstanten (Michaelis-Konstanten) für CO2 und O2 [μmol/m2/s], Jmax, Vmax=maximale Reaktionsgeschwindigkeiten.
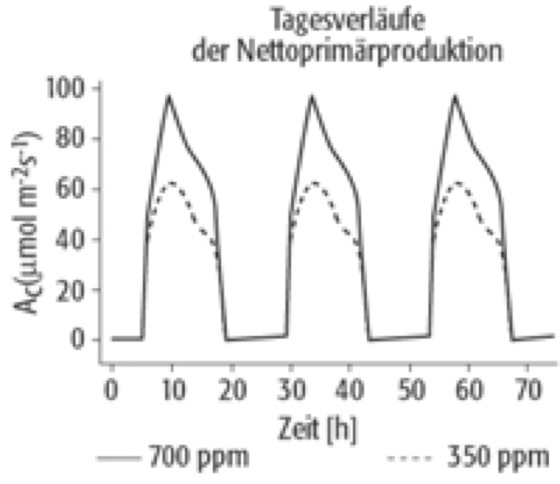
Dieses Modell lässt sich auf die Produktion von Pflanzenbeständen erweitern, indem die Bestandesgeometrie (Überlappung der Blätter, beschatteter Bereich usw.) berücksichtigt wird. Durch temperaturabhängige Formulierung der Prozessparameter steht somit ein Modell zur Verfügung, das es erlaubt, die potenzielle Primärproduktion in Abhängigkeit vom CO2-Angebot, der Strahlung und der Temperatur zu berechnen. Damit ist es auch möglich, das Modell in einem geographischen Kontext anzuwenden. Abbildung 3 zeigt Tagesverläufe der Nettoprimärproduktion bei zwei unterschiedlichen CO2-Konzentrationen.
Die Zustandsvariablen der Kompartimentansätze enthalten keine expliziten räumlichen Abhängigkeiten. Im Rahmen dieser Konzeption können Transportprozesse durch eine Verfeinerung der Kompartimentstruktur und räumliche Zuordnung der Kompartimente modelliert werden. Ökosysteme weisen kontinuierliche und diskrete Prozessstrukturen auf.
Bei der Kopplung von Bestandesdynamik und Wasser- und Stofftransport z.B. werden die physiologischen Prozesse durch ein Kompartimentschema (s.o.) modelliert, während die Transportprozesse kontinuierlich sind und daher durch partielle Differenzialgleichungen beschrieben werden. Die mathematische Struktur des Systems Boden-Pflanze ist daher heterogen.
Um die Stoffbilanzen von Landschaftsausschnitten zu berechnen, wird das Gebiet in Ökotope (s.o.) eingeteilt (kartographisches Modellieren, GIS). Für jede Einheit werden die Stoffströme berechnet, wobei lateraler Austausch durch Kopplung der Ökotopmodelle über Interflow in der vadosen Zone und/oder durch ein unterliegendes großmaßstäbiges dreidimensionales Modell für den Stofftransport in Aquiferen realisiert wird.
OR
ökologische Modellbildung 1: ökologische Modellbildung 1: Kompartimentschema für die Material-und Energieflüsse in einem minimalen Ökosystem, bestehend aus den Komponenten Primärproduzenten (PP), Herbivoren (H), Karnivoren 1. Ordnung (K1), Karnivoren 2. Ordnung (K2), Bestandsabfall (BA) und Destruenten (D).
![](javascript:ShowPic("/lexika/images/geogr/oe_m_bi1.jpg", "643", "496");)
ökologische Modellbildung 2: ökologische Modellbildung 2: Mathematische Ansätze für die Flüsse.
![](javascript:ShowPic("/lexika/images/geogr/toe_m_bi.jpg", "500", "407");)
ökologische Modellbildung 3: ökologische Modellbildung 3: Effekt einer CO2-Erhöhung auf die Nettoprimärproduktion (35° nördlicher Breite, Anfang Juli).
![](javascript:ShowPic("/lexika/images/geogr/oe_m_bi2.jpg", "200", "173");)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.