Lexikon der Geowissenschaften: Boulton-Verfahren
Boulton-Verfahren, ein Typkurvenverfahren zur Auswertung von instationären Pumpversuchen in Grundwasserleitern mit verzögerter Entleerung. Ein halbfreier Grundwasserleiter ist ein Grundwasserleiter, der von einer geringer, aber ebenfalls wasserleitenden Schicht überlagert wird ( Abb. 1 ). Führt man in ihm einen Pumpversuch durch, so gliedert sich die Absenkung in drei Phasen:
1. Phase: Die Absenkung verläuft wie im gespannten Grundwasserleiter; das geförderte Wasser stammt aus der Druckentlastung des Grundwassers und aus der Kompression des Korngerüsts. Diese Phase dauert meist nur einige Minuten. 2. Phase: Hier stellt sich durch ein der Leckage im halbgespannten Grundwasserleiter vergleichbares Nachtropfen aus der überlagernden Schicht ein pseudostationärer Zustand ein; die Absenkungskurve verflacht immer mehr, weshalb ein halbfreier Grundwasserleiter oft auch als Grundwasserleiter mit verzögerter Entleerung und der Effekt als verzögerte Porendränung bezeichnet wird. Diese Phase dauert im Bereich von Minuten bis zu einigen Stunden. 3. Phase: Der Einfluß der verzögerten Entleerung wird zunehmend geringer, so daß die Absenkungskurve wieder steiler wird und nur noch horizontale Strömungskomponenten wirksam sind. Die Absenkung verläuft nun wie in einem freien Grundwasserleiter und die Werte müssen bei hohen Absenkungsbeträgen zur Auswertung korrigiert werden (korrigierte Absenkung). Sind die Verhältnisse ideal, so können die Phasen 1 und 3 auch getrennt nach dem Verfahren von Theis für gespannte bzw. freie Grundwasserleiter ausgewertet werden. Ist der Durchlässigkeitsunterschied zu gering oder der Brunnendurchmesser groß, so dauern die Phasen 1 und 2 nicht lange genug für eine getrennte Auswertung.
Boulton hat ein Verfahren vorgestellt, das das oben beschriebene Verhalten eines halbfreien Grundwasserleiters mittels eines empirisch ermittelten Boultonschen Verzögerungs-Indexes beschreibt. Die Brunnenformel nach Boulton lautet:
mit
und
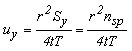
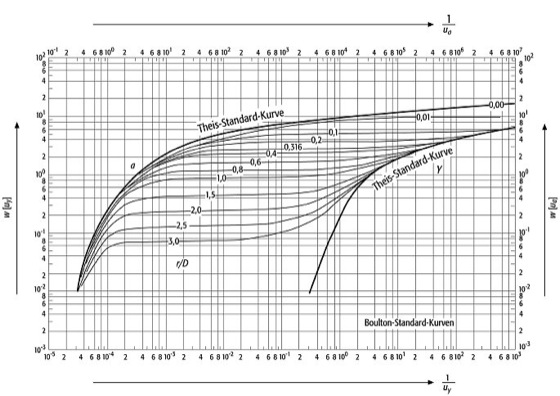
(s = Absenkung; Q = Förderrate; W(ua, uy, r/D) = Brunnenfunktion für halbfreie Grundwasserleiter; r = Abstand zwischen Meßstelle und Förderbrunnen; D = Dränfaktor; S = Speicherkoeffizient für 1. Phase; Sy = Speicherkoeffizient für 3. Phase ist gleich nsp = speicherwirksamer Porenanteil, t = Zeit). Die graphische Auswertung erfolgt ähnlich wie beim Theisschen Typkurvenverfahren durch Anpassung der Datenkurve an die Typkurve der Modellfunktion. Dazu wird W(ua, r/D) gegen 1/ua und W(uy, r/D) gegen 1/uy doppeltlogarithmisch für verschiedene Werte von r/D aufgetragen. Hierdurch ergibt sich eine Schar von Typkurven ( Abb. 2 ).
Zur Auswertung eines Pumpversuchs trägt man in einem ersten Arbeitsschritt die gemessenen Absenkungsbeträge s gegen die zugehörigen Zeiten t auf doppeltlogarithmischen Papier für eine bestimmte Meßstelle im Abstand r auf. Durch achsenparalleles Verschieben der Datenkurve gegen die Typkurve erfolgt nun die Anpassung getrennt in zwei Schritten für die 1. und 3. Phase. Zuerst wird die 1. Phase der Datenkurve an die am besten passenden Kurve (W(ua, r/D)-1/ua) der Typkurvenschar angepaßt, der r/D-Wert dieser Kurve notiert und ein match pointA bestimmt. Für den match point A wird nun W(ua, r/D), 1/ua, s und t abgelesen. Mit den weiter oben angeführten Gleichungen können nun die Transmissivität T (und daraus bei bekannter wassererfüllter Mächtigkeit der Durchlässigkeitsbeiwert kf) und der Speicherkoeffizient S für die Phase 1 bestimmt werden. Danach wird die 3. Phase der Datenkurve an den W(uy, r/D)-1/uy-Teil der Kurve für dasselbe r/D angepaßt und ein match point B ausgewählt, für den W(uy, r/D), 1/uy, s und t abgelesen werden. Mit diesen Werten wird nun die Transmissivität T (bzw. der Durchlässigkeitsbeiwert kf) und der Speicherkoeffizient Sy = nsp für die Phase 3 berechnet. Dabei sollte sich für T ungefähr der gleiche Wert wie aus der 1. Phase ergeben. Über die Gleichung
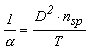
kann nun der Boultonsche Verzögerungsindex1/α berechnet werden. Aus Verzögerungsindex und bekanntem r/D-Wert läßt sich über die Verzögerungs-Index-Kurve die Zeit t0 bestimmen, nach deren Ablauf die verzögerte Porendränung keinen Einfluß mehr auf den Absenkungsverlauf ausübt.
Für das Verfahren nach Boulton muß neben den bei Theis getroffenen Annahmen noch eine weitere Voraussetzung erfüllt sein. Der Grundwasserleiter zeigt das Phänomen der verzögerten Entleerung und die Strömung im Grundwasserleiter ist überall praktisch horizontal. In der Praxis wird heute bei der Auswertung von Pumpversuchen in halbfreien Grundwasserleitern das Typkurvenverfahren von Neuman bevorzugt. Es ist eine Weiterentwicklung des von Boulton vorgestellten Verfahrens. Es ersetzt den Verzögerungs-Index, welcher keine direkten Rückschlüsse auf die Eigenschaften des Grundwasserleiters zuläßt, durch einen Parameter β, der direkt die hydraulischen Eigenschaften des Grundwasserleiters beschreibt. [WB]
Literatur: [1] DAWSON, K.J. & ISTOK, J.D. (1991): Aquifer Testing. Design and Analysis of Pumping and Slug Tests. – Chelsea. [2] LANGGUTH, H.-R. & VOIGT, R. (1980): Hydrogeologische Methoden. – Berlin, Heidelberg, New York.
Boulton-Verfahren 1: halbfreier Grundwasserleiter und Verlauf der Absenkungskurve (r = Abstand zwischen Meßstelle und Förderbrunnen, s = Absenkung, Q = Förderrate). Boulton-Verfahren 1:

Boulton-Verfahren 2: Boulton-Typkurven W(uay, r/D) gegen 1/uay für verschiedene Werte von r/D. Boulton-Verfahren 2:
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.