Lexikon der Geowissenschaften: Suszeptibilität
Suszeptibilität, die magnetische Suszeptibilität χ ist ein Maß für die Fähigkeit eines Materials, in einem äußeren Magnetfeld Ha eine (induzierte) Magnetisierung Mi zu erwerben, die nach der Entfernung von Ha aber sofort wieder verschwindet. Es ist: χ=Mi/Ha. Diamagnetische Stoffe haben eine negative Suszeptibilität, sie werden in einem inhomogenen Magnetfeld aus dem Gebiet hoher Feldstärke herausgedrängt. Paramagnetische, ferromagnetische, antiferromagnetische und ferrimagnetische Substanzen besitzen eine positive Suszeptibilität und werden bei inhomogenen Feldern in das Gebiet hoher Feldstärken hineingezogen. Diese Kräfte inhomogener Magnetfelder werden zur Messung der Suszeptibilität genutzt. Während die Suszeptibilität diamagnetischer Stoffe von der Temperatur unabhängig ist, wird χ(T) aller anderen Stoffe durch das Curie-Gesetz bzw. das Curie-Weiss-Gesetz beschrieben. Ferro- und Ferrimagnetika zeigen dicht unterhalb ihrer Curie-Temperatur ein Maximum von χ, das Hopkinson-Maximum. Der Anstieg der Neukurve in einer Hysteresekurve wird als Anfangssuszeptibilität χa bezeichnet. Die Suszeptibilität bezogen auf die Masse einer Probe nennt man die spezifische Suszeptibilität. Sie wird in Einheiten [m3/kg] gemessen, während die auf das Volumen bezogene Suszeptibilität in allen Maßsystemen dimensionslos ist. In SI-Einheiten wird χ häufig in [m3/m3], in cgs-Einheiten in [cm3/cm3] angegeben. Es gilt:
1 [cm3/cm3]=4·π[m3/m3].
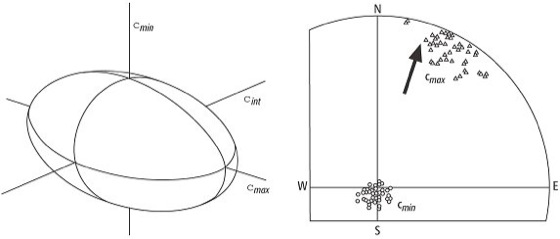
Nur bei isotropen Materialien, dazu zählen auch die kubisch kristallisierenden Minerale wie z.B. Magnetit, Maghemit, die Titanomagnetite und die Granate, ist χ richtungsunabhängig und eine skalare Größe, sonst ein Tensor zweiter Stufe. Bei den meisten paramagnetischen (z.B. Hornblende, Biotit, Olivin) und auch einigen ferrimagnetischen Mineralen (z.B. Magnetkies, Hämatit) ist χ anisotrop. Das Suszeptibilitätsellipsoid mit den drei Hauptachsen χmax, χint, χmin ( Abb.) hat eine oblate (diskusartige) Form, wenn χmax ≈ χint > χmin, und ist prolat (zigarrenförmig), wenn χmax > χint ≈ χmin. Als mittlere Suszeptibilität bezeichnet man das arithmetische Mittel χ=(χmax+χint+χmin)/3.
Zur Beschreibung des Grades der Anisotropie der Suszeptibilität werden im Gesteinsmagnetismus folgende Größen verwendet: Anisotropiegrad P=χmax/χmin; Foliationsfaktor F=χint/χmin; Lineationsfaktor L=χmax/χint. Im Flinn-Diagramm werden die beiden Anisotropiegrade L und F gegeneinander aufgetragen. Das Verhältnis:
K=L/F=χmax·χmin/χint2
ermöglicht sowohl eine Unterscheidung von prolaten (L > F), oblaten (L F) und neutralen (K=L/F=1) Formen als auch die Darstellung der Anisotropiegrade. Auch bei den von Natur aus isotropen ferrimagnetischen Mineralen kann eine Anisotropie der Suszeptibilität auftreten, wenn die Kornform von der Kugelgestalt abweicht (Formanisotropie). Prolate Formen wie z.B. nadelförmige Kristalle haben in Richtung der langen Achse eine größere Suszeptibilität als senkrecht dazu. Bei oblaten Kristallformen ist in der Richtung senkrecht zur Scheibe die Suszeptibilität minimal während χmax und χint innerhalb der Ebene der Scheiben liegen.
Die Anisotropie der Suszeptibilität von Gesteinen hängt davon ab, wie die durch Kristallanisotropie anisotropen paramagnetischen und die durch Formanisotropie oder Kristallanisotropie anisotropen ferrimagnetischen Minerale orientiert sind. Bei einer völlig regellosen Anordnung sämtlicher Kristalle eines Gesteins ist χ isotrop. Dies trifft in der Regel für die magmatischen Tiefengesteine wie Granit oder Gabbro zu. Bei geschichteten Gesteinen (Sedimenten, kristalline Schiefer) liegen χmax und χint in der Regel innerhalb der Sedimentationsebene bzw. der Schieferungsebene und χmin senkrecht dazu. Bei Gesteinen mit einem Fließgefüge (z.B. extrusive Magmatite, fluviatile Sedimente) charakterisiert χmax die Fließrichtung ( Abb.). [HCS]
Suszeptibilität: Suszepbilitätsellipsoid mit χmax, χint und χmin (links) und Ausrichtung von χmax und χmin bei einem Sediment mit bekannter Schüttungsrichtung (Pfeil). χmin steht senkrecht auf der Sedimentationsebene (rechts). Suszeptibilität:
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.