Lexikon der Geowissenschaften: trigonometrische Höhenbestimmung
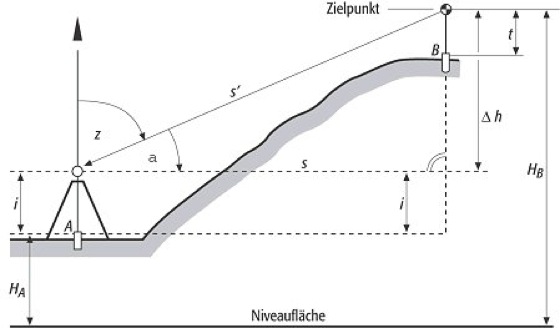
trigonometrische Höhenbestimmung, trigonometrischeHöhenmessung, geodätisches Meßverfahren zur Bestimmung von Höhenunterschieden mittels trigonometrischer Funktionen ( Abb. 1). Man unterscheidet trigonometrische Höhenmessungen über kurze Distanzen ( 250 m) und über größere Distanzen ( 10 km). a) Trigonometrische Höhenmessung über kurze Distanzen: Es werden von einem Standpunkt A, dessen Höhe (HA) bekannt ist, z.B. mit einem Theodoliten, zu einem Punkt B, dessen Höhe (HB) bestimmt werden soll, der Höhenwinkel α oder der Zenitwinkel Z und die Distanz s' oder die Strecke S gemessen bzw. ermittelt und die Instrumentenhöhe i auf dem Standpunkt A sowie die Zielhöhe t auf dem Punkt B gemessen. Der Höhenunterschied Δh ergibt sich zu:
Δh=scotz, Δh=s'cosz bzw.
Δh=stanα, Δh=s'sinα.
Die Höhe des Punktes B erhält man durch:
HB=HA+i+Δh-t.
Kann zu dem Punkt, dessen Höhe bestimmt werden soll, die Distanz oder die Strecke nicht gemessen werden, so kommt bei der trigonometrischen Höhenmessung die sogenannte Turmhöhenbestimmung mit Hilfe eines vertikalen oder horizontalen Hilfsdreiecks zur Anwendung ( Abb. 2). Bei der Verwendung eines vertikalen Hilfsdreiecks müssen die Standpunkte A und B für das Instrument und der höhenmäßig zu bestimmende Punkt P (z.B. Turmspitze) etwa eine Vertikalebene bilden. Die Höhen der Standpunkte (HA, HB) müssen bekannt sein, die Instrumentenhöhen (iA, iB) sowie die Höhenwinkel (αA, αB) oder Zenitwinkel (zA, zB) müssen gemessen werden. Der Höhenunterschied Δh ergibt sich z.B. mit den gemessenen Zenitwinkeln zu
wobei a der Höhenunterschied der Kippachsen zwischen den aufgestellten Theodoliten auf A und B ist. Die Höhe des Punktes (HP) berechnet sich
HP=HB+iB+Δh
und/oder
HP=HA+iA+Δh+a.
Ist es im Gelände möglich, mit den Standpunkten A und B und dem höhenmäßig zu bestimmenden Punkt P etwa ein gleichseitiges horizontales Dreieck zu bilden ( Abb. 3), so kann mit diesem ebenfalls eine trigonometrische Höhenmessung vorgenommen werden. Wie bei der Anwendung eines vertikalen Dreiecks müssen die o.g. Bestimmungsgrößen gegeben sein und gemessen werden. Zusätzlich sind die horizontalen Winkel α und β zu ermitteln. Im horizontalen Dreieck A'B'P' lassen sich die Strecken von:
mittels Sinussatz berechnen:
Die Höhenunterschiede ΔhA und ΔhB berechnen sich jeweils aus den vertikalen Dreiecken zu ΔhA=dA·cotzA und ΔhB=dB·cotzB. Die Höhe HP wird zur Kontrolle zweimal berechnet:
HP=HA+iA+ΔhA und HP=HB+iB+ΔhB.
Mit Hilfe der trigonometrischen Höhenmessung lassen sich auch Höhenunterschiede entlang einer Linie in Form eines Zuges analog zum Nivellement übertragen ( Abb. 4). Hierbei steht ein Tachymeter zwischen dem Punkt A und dem Punkt B und der Höhenunterschied (Δh) wird aus den gemessenen Größen, z.B. Zenitwinkeln, Distanzen und den Zielhöhen (tr und tv), aus den Rückmessungen zum Punkt A und den Vorblickmessungen zum Punkt B ermittelt. Der Höhenunterschied des Rückblicks r und des Vorblicks v ergibt sich:
r=tr–sr·cotzr und v=tv-sv·cotzv.
Der Höhenunterschied zwischen r und v bzw. A und B ergibt sich:
Δh=sv·cotzv-sr·cotzr+tr-tv.
Das trigonometrische Nivellement hat gegenüber dem geometrischen Nivellement den Vorteil, durch Schrägzielungen größere Strecken überbrücken zu können. Aufgrund der hohen Meßgenauigkeit der elektronischen Tachymeter erreicht man die Genauigkeiten des geometrischen Nivellements. Im bewegten Gelände und bei Zielungen über große Distanzen ist das trigonometrische Nivellement wirtschaftlicher als das geometrische. Werden bei einem Polygonzug zusätzlich die Höhen- oder Zenitwinkel zwischen den Polygonpunkten bestimmt und die Höhen trigonometrisch berechnet, erhält man einen Höhenpolygonzug. b) Trigonometrische Höhenmessungen über größere Distanzen ( Abb. 5): Hierbei muß zur Berechnung des Höhenunterschiedes ΔH unter Verwendung einseitiger Zenitwinkelmessungen der Einfluß der Erdkrümmung:
und Refraktionseinfluß:
berücksichtigt werden, wobei der Erdradius R=6380 km und der Refraktionskoeffizient k ≈ 0,13 ist. Die Höhenbestimmung mit der Distanz D oder mit der Strecke S im Bezugshorizont ergibt sich zu:
oder:
wobei i=Instrumentenhöhe und t=Zieltafelhöhe ist. Darüber hinaus muß im Rahmen der Auswertung trigonometrischer Höhenmessungen der Einfluß der Lotabweichung auf die gemessenen Zenitwinkel berücksichtigt werden, d.h., die Berechnung ist auf das Ellipsoid zurückzuführen. Bei der Anwendung der trigonometrischen Höhenmessung im Gebirge stellen die reliefbedingten Unregelmäßigkeiten des Schwerefeldes die wesentlichen Unsicherheiten dar. Bei gegenseitig gleichzeitiger Zenitwinkelmessung und bei stabilen Wetterlagen, läßt sich der Refraktionseinfluß weitgehend eliminieren. Bei Messungen bis zu 10 km Länge und Berücksichtigung der Lotabweichungseinflüsse lassen sich Genauigkeiten:
mit L in km und σH in cm erreichen. [KHK]
trigonometrische Höhenbestimmung 1: Schema der trigonometrischen Höhenbestimmung (Δh=Höhenunterschied, A=Standpunkt, HA=Höhe des Standpunktes, B=Zielpunkt, HB=Höhe des Zielpunktes, α=Höhenwinkel, Z=Zenitwinkel, s'=Distanz, S=Strecke, i=Instrumentenhöhe auf dem Standpunkt, t=Instrumentenhöhe auf der Zielhöhe). trigonometrische Höhenbestimmung 1:
![](javascript:ShowPic("/lexika/images/geo/f5f2230.jpg", "449", "263");)
trigonometrische Höhenbestimmung 2: Turmhöhenbestimmung mit vertikalem Hilfsdreieck (ΔH=Höhenunterschied, A,B=Standpunkte, P=zu bestimmender Punkt, HA,HB=bekannte Höhe der Standpunkte, s=bekannte Strecke, x=zu bestimmende Strecke, zA,zB=Zenitwinkel, αA,αB=Höhenwinkel, iA,iB=Instrumentenhöhe). trigonometrische Höhenbestimmung 2:
![](javascript:ShowPic("/lexika/images/geo/f5f2231.jpg", "577", "282");)
trigonometrische Höhenbestimmung 3: Turmhöhenbestimmung mit horizontalem Hilfsdreieck (ΔH=Höhenunterschied, A und B=bekannte Punkte, P=zu bestimmender Punkt, A',B',C'=Hilfsdreieck, α,β=gemessene Winkel). trigonometrische Höhenbestimmung 3:
![](javascript:ShowPic("/lexika/images/geo/f5f2232.jpg", "428", "454");)
trigonometrische Höhenbestimmung 4: trigonometrisches Nivellement (Δh=Höhenunterschied, tr=Zielhöhe im Rückblick, tv=Zielhöhe im Vorblick, sr=Strecke im Rückblick, sv=Strecke im Vorblick, zr=Zielung im Rückblick, zv=Zielung im Vorblick). trigonometrische Höhenbestimmung 4:
![](javascript:ShowPic("/lexika/images/geo/f5f2233.jpg", "451", "239");)
trigonometrische Höhenbestimmung 5: Höhenbestimmung über große Distanzen (Strecken 10km) mit einseitiger Zenitwinkelmessung (ΔH=Höhenunterschied, D=Distanz, S=Strecke, R=Radius, k=Refraktionskoeffizient). trigonometrische Höhenbestimmung 5:
![](javascript:ShowPic("/lexika/images/geo/f5f2234.jpg", "440", "406");)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.