Lexikon der Kartographie und Geomatik: Gradmessung
Gradmessung, E measurement of a degree, Methode, aus der Länge eines Bogens auf der Erdoberfläche die Geometrie des Erdkörpers abzuleiten. Der Begriff Gradmessung rührt daher, dass ursprünglich eine Bogenlänge gemessen werden sollte, die, bei Voraussetzung der Kugelgestalt, im Erdmittelpunkt einem Zentriwinkel von einem Grad entsprach.
Nachdem mehr als 500 Jahre v. Chr. die Erde von Pythagoras als Kugel erklärt worden war, versuchten Gelehrte mittels der in Abb. 1 skizzierten Weise den Erdradius zu bestimmen. Aus den astronomischen Breitenbestimmungen in A und B und dem Abstand mAB folgt für den Radius R einer kugelförmig gedachten Erde: 
Der bekannteste Versuch wurde von Eratosthenes (276-195 v. Chr.) zwischen Assuan und Alexandria erfolgreich ausgeführt. Im weiteren Verlauf sind (1.) Breiten- und (2.) Längengradmessungen sowie (3.) Gradmessungen schief zum Meridian zu unterscheiden.
1. Breitengradmessungen: Die Weiterentwicklung der Methode durch die Verwendung von Dreiecksketten (Triangulation nach W. Snellius, 1615) erlaubte eine genauere Entfernungsbestimmung, als es vorher möglich war. So wiesen die Ergebnisse der Gradmessungen französischer Gelehrter (Picard, Lahire, Cassini) im 17. Jh. darauf hin, dass die Erdform elliptisch ist. Allerdings deuteten die Messungen ein "eiförmiges" Ellipsoid an. Dieses Ergebnis widersprach der Beobachtung J. Richers (1672), dass eine in Paris richtig gehende Pendeluhr in Cayenne nachging. Die Eiform widersprach auch den theoretischen Überlegungen I. Newtons (1687) und C. Huygens' (1690). Erst als die französische Akademie zwei Expeditionen ausrüstete und eine 1736/37 unter Maupertuis und Clairaut nach Lappland (+66°20′ Breite) und die andere 1735/41 unter Godin, La Condamine und Bouguer nach Peru (-1°31′ Breite) entsandte, konnte die am Pol abgeplattete, ellipsoidische Form des Erdkörpers prinzipiell nachgewiesen werden (Abb. 2 ). Die metrischen Längen der aus den Dreiecksketten abgeleiteten Meridianbögen entsprachen in Lappland einem Breitenunterschied von 57,5′ und in Peru von 3°07′. Mit den Ergebnissen dieser beiden Gradmessungen war das an den Polen abgeplattete Rotationsellipsoid mit seinen Halbachsen a und b nachgewiesen, wenn auch die Abplattung mit: 
wesentlich zu groß erhalten worden war. Wegen der Formunterschiede zwischen dem damals noch nicht erkannten Geoid und einem Ellipsoid (vgl. Lotabweichung) ergab sich eine Achsenverkürzung des Ellipsoids. Die jeweils vermessenen Dreiecksketten verliefen nur etwa längs eines Meridians. Durch astronomische Azimutmessungen in ihren Endpunkten war es möglich, eine Reduktion der Längen auf den Meridian vorzunehmen.
2. Längengradmessungen: Dreiecksketten, die unter einem kleinen Winkel zu einem Parallelkreis verlaufen, können nicht auf einen Meridian reduziert werden. Die Reduktion auf einen Parallelkreis erfordert aber neben den Messungen des astronomischen Azimuts α1, α2 und den astronomischen Breitenmessungen (φ1), (φ2) auch genaue astronomische Zeit- und Längenbestimmungen. Aus Längengradmessungen können große und kleine Halbachse der Meridianellipse oder die große Halbachse und die Abplattung 
bzw. die Exzentrizität 
ebenfalls abgeleitet werden. Dreiecksketten längs eines Parallels erfordern astronomische Bestimmungen der Ortszeit zumindest am Anfangs- und am Endpunkt, als deren Differenz sich der Längenunterschied Δλ (Abb. 3) ergibt. Solche Zeitübertragungen mussten bis zur Einführung der über Rundfunk ausgestrahlten Zeitzeichen etwa um 1930 durch sorgfältig ausgeführte Uhrentransporte realisiert werden.
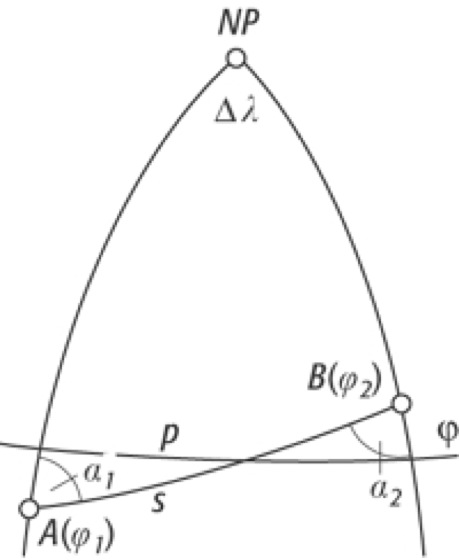
3. Gradmessungen schief zum Meridian: Wenn an den Endpunkten eines Bogens die Breiten und Längen und damit der Längenunterschied gemessen sind, kann die Kette sowohl als Meridian-, wie als Parallelbogen berechnet werden. Diese Gradmessung schief zum Meridian wurde erstmals von Bessel bei seiner Gradmessung in Ostpreußen angewendet.
Mitte des 19. bis Mitte des 20. Jhs. sind global zahlreiche großräumige Gradbogenmessungen ausgeführt und zu Ketten von Dreiecksnetzen oder zu Flächennetzen zur Ableitung bestanschließender Ellipsoide und zur Bestimmung des Geoids weiterentwickelt worden (Bessel, Hayford, Krassowski). In die Triangulation wurden zahlreiche Basisnetze (Basis) und Laplacepunkte eingeschlossen. Wegen der großen Ozeangebiete war ein globales Triangulationsnetz nicht realisierbar, sodass die Ableitung eines mittleren Erdellipsoids erst mit Hilfe der Satellitengeodäsie möglich geworden ist.
KST
Literatur: JORDAN & EGGERT & KNEISSL (1969): Handbuch der Vermessungskunde, Bd. V von K. LEDERSTEGER, Stuttgart.
Gradmessung 1:Gradmessung 1: Prinzip der Breitengradmessung (mAB = Kreisbogenstück zwischen den Punkten A und B, R = Radius, φ1,φ2 = Koordinaten der Punkte A und B, 0 = Koordinatenursprung).
![](javascript:ShowPic("/lexika/images/karto/gradme1.jpg", "200", "199");)
Gradmessung 2:Gradmessung 2: Breitengradmessungen zur Bestimmung des ellipsiodischen Erdgestalt (a, b = Halbachsen, M, M ′ = Meridiankrümmungsradien, m, m ′ = Kreisbogenstükke, φ1,φ2, φ1 ′,φ2 ′ = geographische Koordinaten, Δ φ, Δ = Differenzen zwischen φ1 und φ2 bzw. φ1′ und φ2′, 0 = Koordinatenursprung.
![](javascript:ShowPic("/lexika/images/karto/gradme2.jpg", "300", "279");)
Gradmessung 3:Gradmessung 3: Gradmessung schief zum Meridian. (NP = Nordpol, p = Parallelkreis der Breite φ, s = Großkreisbogen zwischen A und B, α1, α2 = Schnittwinkel von s mit dem Meridian, Δ λ = Differenz der Koordinaten).
![](javascript:ShowPic("/lexika/images/karto/gradme3.jpg", "200", "244");)
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.