Lexikon der Mathematik: ϵ-Präferenz
eine Präferenzrelationen von Fuzzy- Mengen.
Eine Fuzzy-Menge \(\tilde{B}\) wird einer Fuzzy-Menge \(\tilde{C}\) auf dem Niveau ϵ ∈ [0, 1] vorgezogen, und man schreibt \(\tilde{B}\,{\succ }_{\varepsilon }\tilde{C}\), wenn ϵ die kleinste reelle Zahl ist, so daß
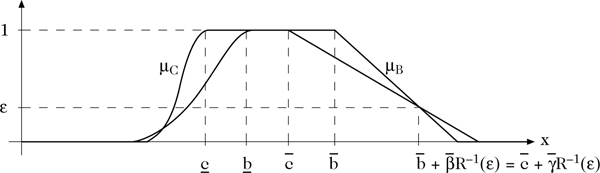
ϵ-Präferenz zwischen zwei L-R-Fuzzy-Intervallen \(\begin{eqnarray}\tilde{B}={(\underline{b};\bar{b};\underline{\beta };\bar{\beta })}_{LR}\end{eqnarray}\) und \(\tilde{C}={(\underline{c};\bar{c};\underline{\gamma };\bar{\gamma })}_{LR}\)
Für L-R-Fuzzy-Intervalle \(\begin{eqnarray}\tilde{B}={(\underline{b};\bar{b};\underline{\beta };\bar{\beta })}_{LR}\end{eqnarray}\) und \(\tilde{C}={(\underline{c};\,\bar{c};\,\underline{\gamma };\,\bar{\gamma })}_{LR}\) lassen sich die Bedingungsungleichungen der ϵ-Präferenz vereinfachen zu
Für Fuzzy-Intervalle
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.