Verdichtung von Histogrammen unter Verwendung empirischer Quantile.

Dabei werden von einer Stichprobe der maximale und minimale Wert x_max bzw. x_min sowie der empirische Median x_0,5 und die empirischen Quartile x_0,25 und x_0,75 berechnet und in einer Box (die Breite der Box ist unerheblich) dargestellt, wie die nachfolgende Abbildung zeigt.

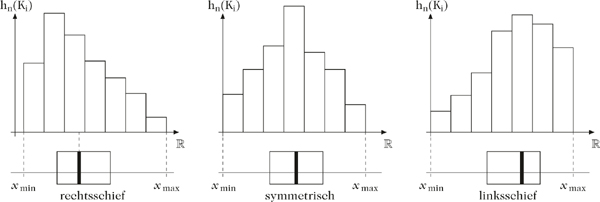
In jedem Abschnitt des Box-Plots liegen 25 Prozent der beobachteten Stichprobendaten. Mit Hilfe der Box-Plots kann man Schlüsse über die Symmetrie von Verteilungen ziehen, wie die nächste Abbildung zeigt.

Mit Hilfe von Box-Plots kann man auch sehr bequem viele Häufigkeitsverteilungen gleichzeitig miteinander vergleichen.

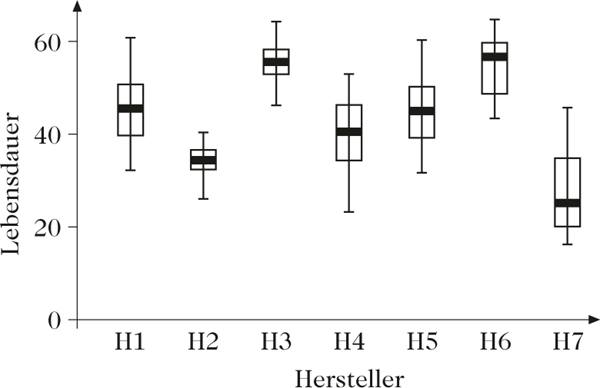
In der dritten Abbildung sind die Lebensdauerverteilungen von Motoren verschiedener Hersteller, die auf der Basis von Stichprobendaten ermittelt wurden, dargestellt. Wie man leicht erkennen kann, sind beispielsweise ca. 75 Prozent der betrachteten Motoren von Hersteller 1 besser als die von Hersteller 2, während 50 Prozent der Motoren von Hersteller 1 eine kürzere Lebensdauer besitzen als die von Hersteller 3.