ineinander überführbare Komplexmorphismen.

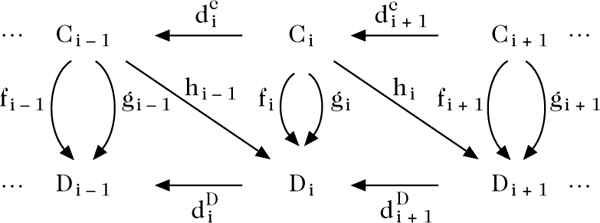
Seien f, g : C_• → D_• Komplexmorphismen zwischen zwei Komplexen (abelscher Gruppen, Vektorräume, etc.) mit den Objektabbildungen f_i, g_i : C_i → D_i für i ∈ ℤ. Sie heißen homotop, falls es eine Familie h_i : C_i → D_i+1 gibt mit \begin{eqnarray}{f}_{i}-{g}_{i}={d}_{i+1}\circ {h}_{i}+{h}_{i-1}\circ {d}_{i}.\end{eqnarray}

Die Familie h = (h_i) heißt eine Homotopie zwischen f und g. Homotope Komplexmorphismen definieren dieselben Abbildungen auf den Homologiegruppen \begin{eqnarray}{\bar{f}}_{n},{\bar{g}}_{n}:{\text{H}}_{n}(C\bullet )\to {H}_{n}(D\bullet ).\end{eqnarray}

Die entsprechenden Definitionen gelten auch für Kokomplexe. Die Homotopieabbildungen sind dann definiert als h_i : C_i → D_i−1.