die durch die hypergeometrischen Funktionen F definierten Funktionen

\begin{eqnarray}{P}_{v}^{-\mu }(z):={\left(\frac{z-1}{z+1}\right)}^{\mu /2}\\ F\left(v+1,-v;\mu +1,\frac{1-z}{2}\right)\\ ={2}^{-v}{\left(\frac{z-1}{z+1}\right)}^{\mu /2}\\ F\left(\mu -v,v+\mu +1;\mu +1,\frac{1-z}{2}\right)\end{eqnarray}

und

\begin{eqnarray}{Q}_{v}^{\mu }(z)={2}^{v}\Gamma (v+1)(\frac{{(z-1)}^{(\mu /2)-v-1}}{{(z+1)}^{\mu /2}})\\ F\left(v+1,v-\mu +1;2v+2;\frac{2}{1-z}\right)\\ ={2}^{v}\Gamma (v+1)(\frac{{(z+1)}^{(\mu /2)}}{{(z-1)}^{(\mu /2)+v+1}})\\ F\left(v+1,v+\mu +1;2v+2;\frac{2}{1-z}\right).\end{eqnarray}

Es handelt sich um sind zwei linear unabhängige Lösungen der Legendre-Differentialgleichung in komplexer Notation

\begin{eqnarray}(1-{z}^{2})\frac{{d}^{2}w}{d{z}^{2}}-2z\frac{dw}{dz}+\left(v(v+1)-\frac{\mu }{1-{z}^{2}}\right)w=0.\end{eqnarray}

Dabei heißt ν der Grad und µ die Ordnung der Legendre-Funktion, wobei sowohl für ν als auch für µ alle Zahlen aus ℂ zugelassen sind.

Mitunter findet man in der Literatur auch andere Konventionen bei der Wahl der Vorfaktoren. Die hier verwendete Notation ist der in [3] angeglichen.

\({P}_{v}^{-\mu }(z)\) und \({Q}_{v}^{\mu }(z)\) existieren für alle komplexen Werte für µ, ν und z, ausgenommen mögliche Pole bei z = ±1 und z = ∞. Als Funktionen von z sind sowohl \({P}_{v}^{-\mu }\) als auch \({Q}_{v}^{\mu }\) mehrdeutig, mit möglichen Verzweigungspunkten bei z = ±1 und z = ∞, wobei man ihre Hauptzweige durch Aufschneiden der komplexen Ebene entlang der reellen Achse von z = −∞ bis z = 1 durch die Hauptzweige der in den obigen Ausdrücken auftretenden Funktionen definiert.

Für festes z sind die Funktionen \({P}_{v}^{-\mu }(z)\) und \({Q}_{v}^{\mu }(z)\) ganze Funktionen in µ und ν, wiederum ausgenommen die o.g. Punkte. Insbesondere gehen die Funktionen \({P}_{v}^{-\mu }\) für ν = n ∈ ℕ und µ = 0 in die Legendre-Polynome P_n über.

Da die Differentialgleichung bei den Substitutionen µ → −µ oder ν → −ν − 1 in sich selbst übergeht, zeigen die Lösungen auch entsprechende Symmetrierelationen:

\begin{eqnarray}\begin{array}{ll}{P}_{v}^{\mu }={P}_{-v-1}^{\mu } & {P}_{v}^{-\mu }={P}_{-v-1}^{-\mu }\\ {Q}_{v}^{\mu }={Q}_{v}^{-\mu } & {Q}_{-v-1}^{\mu }={Q}_{-v-1}^{-\mu }\end{array}\\ \end{eqnarray}

Man erhält ebenfalls folgende zusätzliche Beziehungen zwischen \({P}_{v}^{-\mu }\) und \({Q}_{v}^{\mu }\):

\begin{eqnarray}\begin{array}{lll}\frac{2\sin (\mu \pi ){Q}_{v}^{\mu }}{\pi } & = & \frac{{P}_{v}^{\mu }}{\Gamma (v+\mu +1)}-\frac{{P}_{v}^{-\mu }}{\Gamma (v-\mu +1)}\\ \frac{2\sin (\mu \pi ){Q}_{-v-1}^{\mu }}{\pi } & = & \frac{{P}_{v}^{\mu }}{\Gamma (\mu -v)}-\frac{{P}_{v}^{-\mu }}{\Gamma (-v-\mu )}\\ \cos (v\pi ){P}_{v}^{-\mu } & = & \frac{{Q}_{-v-1}^{\mu }}{\Gamma (v+\mu +1)}-\frac{{Q}_{v}^{-\mu }}{\Gamma (\mu -v)}\\ \cos (v\pi ){P}_{v}^{\mu } & = & \frac{{Q}_{-v-1}^{\mu }}{\Gamma (v-\mu +1)}-\frac{{Q}_{v}^{\mu }}{\Gamma (v-\mu )}\end{array}\end{eqnarray}

Für die Diskussion von \({P}_{v}^{-\mu }\) und \({Q}_{v}^{\mu }\) als Lösungen einer Differentialgleichung zweiter Ordnung ist ihre Wronski-Determinante von Bedeutung. Man findet:

\begin{eqnarray}\begin{array}{lll}{\mathscr{W}}({P}_{v}^{-\mu }(z),{P}_{v}^{\mu }(z)) & = & -\frac{2\sin (\mu \pi )}{\pi ({z}^{2}-1)}\\ {\mathscr{W}}({P}_{v}^{-\mu }(z),{Q}_{v}^{\mu }(z)) & = & -\frac{1}{\Gamma (v+\mu +1)({z}^{2}-1)}\end{array}\end{eqnarray}

Man kann die Legendre-Funktionen auch durch Integrale in der komplexen Ebene darstellen. Hier zuerst Integraldarstellungen von \({P}_{v}^{-\mu }\text{für}z\rlap{/}{\in }{(-\infty, 1]}\):

\begin{eqnarray}{P}_{v}^{-\mu }(z)=\frac{{e}^{i\mu \pi }\Gamma (-v)}{{2}^{v+1}\pi i\Gamma (\mu -v)}{({z}^{2}-1)}^{\mu /2}\\ \displaystyle \underset{\infty }{\overset{(1+,z+)}{\int }}\begin{array}{c}\frac{({t}^{2}-1)}{{(t-z)}^{v+\mu +1}}dt\\ (\mathrm{Re}(\mu ))\gt (\mathrm{Re}(v))\end{array}\end{eqnarray}\begin{eqnarray}{P}_{v}^{-\mu }(z)=\frac{{2}^{v}{e}^{i\mu \pi }\Gamma (v+1)}{\pi i\Gamma (v+\mu +1)}{({z}^{2}-1)}^{\mu /2}\\ \displaystyle \underset{\infty }{\overset{(1+,z+)}{\int }}\frac{{(t-z)}^{v-\mu }}{{(t-1)}^{v+1}}dt\end{eqnarray}

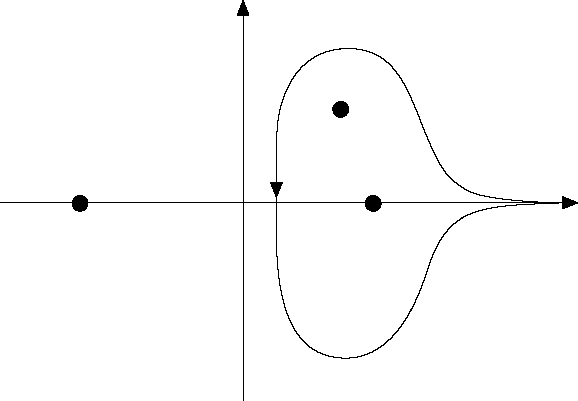
Dabei ist längs eines einfachen geschlossenen Pfades zu integrieren, der von ∞ auf der positiven reellen Achse verläuft, die Punkte t = 1 und t = z impositiven Sinne umschließt, und dann zum Startpunkt zurückläuft, ohne das Intervall (−∞, −1] oder sich selbst zu schneiden.

Für \({Q}_{v}^{\mu }\) erhält man die folgende Integraldarstellung:

\begin{eqnarray}\begin{array}{cc}{Q}_{v}^{\mu }(z) & =\frac{{e}^{-iv\pi }\Gamma (-v)}{{2}^{v+2}\pi i}{({z}^{2}-1)}^{\mu /2}\\ & \displaystyle \underset{a}{\overset{(1+,-1-)}{\int }}\frac{(1-{t}^{2})}{{(z-t)}^{v+\mu +1}}dt\end{array}\end{eqnarray}

Hierbei beginnt der Integrationspfad in einem beliebigen Punkt a im Intervall (−1, +1), umläuft das Intervall (a, 1] einmal im positiven Sinne, kehrt zu a zurück, umläuft das Intervall [−1, a) einmal im negativen Sinne und kehrt abermals zu a zurück. Der Punkt z muß dabei außerhalb der so entstehenden „8“ liegen.

Die folgenden Rekursionsformeln verknüpfen Funktionen \({P}_{v}^{\mu }\) von unterschiedlichem Grad und unterschiedlicher Ordnung miteinander:

\begin{eqnarray}\begin{array}{lll}{P}_{v}^{\mu +2}(z)+2(\mu +1) & = & z{({z}^{2}-1)}^{-1/2}{P}_{v}^{\mu +1}(z)\\ & – & (v-\mu )(v+\mu +1){P}_{v}^{\mu }(z)\\ & = & 0\\ {({z}^{2}-1)}^{-1/2}{P}_{v}^{\mu +1}(z) & = & (v-\mu +1){P}_{v+1}^{\mu }(z)\\ & – & (v+\mu +1)z{P}_{v}^{\mu }(z)\\ {({z}^{2}-1)}^{1/2}{P}_{v}^{\mu /2}(z) & = & (v-\mu ){P}_{v+1}^{\mu +1}(z)\\ & – & (v+\mu +2)z{P}_{v}^{\mu +1}(z)\\ (v+\mu +2){P}_{v+2}^{\mu }(z) & – & (2v+3)z{P}_{v+1}^{\mu }(z)\\ & + & (v+\mu +1){P}_{v}^{\mu }(z)\\ & = & 0\end{array}\end{eqnarray}

Mit Hilfe von Whipples Formel kann man dann entsprechende Relationen für die zweite Lösung \({Q}_{v}^{\mu }\) finden: \begin{eqnarray}{Q}_{v}^{\mu }(z)=\sqrt{\frac{\pi }{2}}{({z}^{2}-1)}^{-1/4}{P}_{-\mu -1/2}^{-v-1/2}(\frac{z}{\sqrt{{z}^{2}-1}})\end{eqnarray}

[1] Abramowitz, M.; Stegun, I.A.: Handbook of Mathematical Functions. Dover Publications, 1972.
[2] Erdélyi, A.: Higher Transcendential Functions, Vol. 2. McGraw-Hill, 1953.
[3] Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, 1974.