Lexikon der Mathematik: Peano-Kurve
ebenenfüllende Kurve, die durch die in der Abbildung angedeutete Konstruktion entsteht.
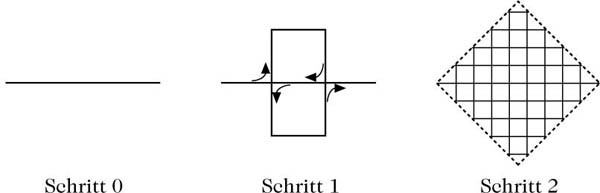
Konstruktion der Peano-Kurve: In jedem Schritt wird ein Geradenstück ersetzt durch 9 andere, deren Länge jeweils ein Drittel der des Ausgangsstücks beträgt.© Springer-Verlag GmbH Deutschland 2017 Bild vergrößern
Die Peano-Kurve P ist eine selbstähnliche Menge mit der Eigenschaft
Man sagt, daß die Peano-Kurve eine ebenenfüllende Kurve ist. Weitere Beispiele für derartige Kurven mit der fraktalen Dimension 2 sind die Hilbert-Kurve und die Peano-Gosper-Kurve. Der Hilbert-Würfel ist das mehrdimensionale Analogon der Hilbert-Kurve.
Copyright Springer Verlag GmbH Deutschland 2017
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.