Teilgebiet der mathematischen Statistik, das diejenigen statistischen Verfahren umfaßt, die zur Qualitätssicherung, vorwiegend zur Qualitätsprüfung und -steuerung verwendet werden.

In den letzten Jahrzehnten ist in der Industrie das Interesse an der Qualitätssicherung der Erzeugnisse stark gewachsen, da ein hoher Qualitätsstandard die Voraussetzung für einen langfristigen Markterfolg ist. Dabei versteht man unter Qualitätssicherung die Gesamtheit aller Tätigkeiten zum Erreichen der Qualität von Produkten. Dazu gehören die Qualitätsplanung, -prüfung und -steuerung. Werden zur Qualitätssicherung Stichproben verwendet und mit den Verfahren der mathematischen Statistik, wie z. B. Tests und Schätzungen, Schlußfolgerungen auf den gesamten Fertigungsprozeß gezogen, so spricht man von der statistischen Qualitätskontrolle (SQK).

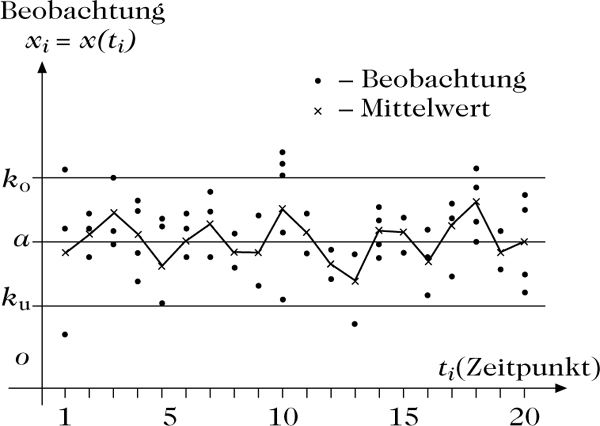
Man unterscheidet zwei grundlegende Aufgaben der SQK: Die statistische Prozeßkontrolle (SPC) und die Annahmestichprobenprüfung (acceptance sampling). Bei der Prozeßkontrolle wird der Fertigungsprozeß mittels sogenannter Kontrollkarten (Regelkarten) laufend überwacht, um während der Produktion Störungen zu entdecken und zu beseitigen. Eine Kontrollkarte ist dabei ein Diagramm von statistischen Kennwerten (z. B. des arithmetischen Mittels, des Medians, oder der Streuung) für eine laufende Folge von Stichproben mit einer Mittellinie (Norm) und den zulässigen Kontroll- oder Toleranzgrenzen K_u, K_o (siehe Abbildung 1). Ein Überschreiten dieser Grenzen führt zum Eingriff in den Produktionsprozeß. Die wichtigste Aufgabe der SQK besteht darin, die Kontrollgrenzen K_u, K_o geeignet festzulegen.

Die Annahmestichprobenprüfung dient zur Überprüfung von Losen (Waren- oder Lieferposten von Erzeugnissen) in der Eingangs-, Zwischen- oder Endkontrolle eines Betriebes, mit dem Ziel, den Ausschußanteil der Produktion zu bestimmen. Dies geschieht anhand von Stichproben mittels sogenannter Stichproben- oder Prüfpläne, die Anweisungen enthalten, mit denen die Annahme oder Zurückweisung eines Loses entschieden wird. Ziel ist es, bei einer hohen Sicherheit der Aussage über den Ausschußanteil den Stichprobenumfang so klein wie möglich zu halten.

Man unterscheidet zwischen einfachen und mehrfachen sowie sequentiellen Stichprobenprüfplänen. Bei letzteren wird nach jedem dem Los entnommenen Stück eine Entscheidung über die Annahme oder Zurückweisung des Loses oder über eine weitere Entnahme entschieden (siehe Abbildung 2). Mathematisch-statistische Grundlage dieser Stichprobenpläne ist die von A. Wald (1947) entwickelte Sequentialanalyse. Bei einer geeigneten Wahl der Annahme- und Ablehnungsgrenzen erhält man mit den sequentiellen Prüf-Verfahren den kleinsten mittleren Stichprobenumfang.

[1] Storm,R.: Wahrscheinlichkeitsrechnung, mathematische Statistik und statistische Qualitätskontrolle. Fachbuchverlag Leipzig-Köln GmbH, 1995.