Interferenzlängenmessung, Methode zur Messung von Längen in Einheiten der Lichtwellenlänge. Diese Vermessung erfolgt entweder direkt, indem die Zahl der Interferenzmaxima oder anderer periodisch wiederkehrender Intensitätswerte gezählt wird, oder indirekt, indem Maßverkörperungen der Länge in einem Interferenzkomparator vermessen oder verglichen werden.

Der direkte Vergleich einer Länge mit der Lichtwellenlänge erfolgt mit Hilfe von Laserwegmeßsystemen, wobei das Licht eines Lasernormals – meist ein Lamb-dip- oder J₂-stabilisierter He-Ne-Laser – zur Beleuchtung eines Michelson-Interferometers verwendet wird (Abb. 1). Die I. beruht darauf, daß sich die Interferenzstreifen bei Bewegung eines der beiden Interferometerspiegel verschieben, wobei einer Verschiebung um einen Streifenabstand eine Änderung der Armlänge um eine halbe Wellenlänge entspricht. In modernen Geräten erfolgt die Zählung der Interferenzstreifen elektronisch, die bei Verschiebung des als Tripelspiegel ausgebildeten Spiegels um die zu messende Strecke einen Referenzpunkt passieren. Durch die Wanderung der Interferenzstreifen über die empfindliche Fläche eines Photodetektors erhält dessen Photostrom einen mit der Frequenz f=2v/λ oszillierenden Anteil. Dabei bezeichnen λ die Wellenlänge und v die (momentane) Geschwindigkeit, mit der sich der Spiegel bewegt. Mißt man daher f, so ergibt sich die Wegstrecke x₂-x₁ daraus durch zeitliche Integration in der Form

, wobei t(x_i) die Zeit bezeichnet, zu der sich der Spiegel am Orte x_i (i=1,2) befindet. Da das photoelektrische Signal einen Gleichspannungsanteil enthält, werden besondere Schaltungen verwendet, um zu reinen Wechselspannungen zu kommen. Ein gängiges Verfahren ist das folgende: Im Ausgange des Michelson-Interferometers werden mittels Polarisationsoptik 4 photoelektrische Signale gewonnen, die um 0°, 90°, 180° und 270° phasenverschoben sind (Abb. 1). Durch geeignete Kombinationen dieser Signale (Abb. 1b) in Differenzverstärkern lassen sich zu sin(2πft) bzw. cos(2πft) proportionale Signale ableiten, die für eine jitter-stabile Vorwärts-Rückwärts-Zählung benötigt werden.

Ein anderes gängiges Verfahren (Abb. 2) nutzt die Frequenzverschiebung, die monochromatisches Licht aufgrund des Doppler-Effektes bei der Reflexion an einem bewegten Spiegel erleidet. Durch Verwendung von 2-Frequenz-Lasern lassen sich dabei Methoden der Heterodyninterferometrie zur Anwendung bringen. Bedingt durch eine Zeeman-Aufspaltung der Laserniveaus sendet der Laser zwei Wellen unterschiedlicher Frequenz ν₁ bzw. ν₂ aus, die in entgegengesetztem Sinne zirkular polarisiert sind. Die Laserstrahlung wird mittels einer λ/4-Platte in zwei senkrecht zueinander polarisierte Wellen verwandelt und einerseits über einen Teiler nebst Polarisator mit einem Photodetektor in eine reine Referenz-Wechselspannung U₀cos(2π[ν₂-ν₁]t) umgewandelt und andererseits zur Beleuchtung eines mit Tripelspiegeln ausgerüsteten Michelson-Interferometers mit einem Polarisationsstrahlenteiler im Eingange benutzt. Dadurch wird erreicht, daß das Licht im Referenz- und im Meßstrahlengange unterschiedliche Frequenzen ν₁ bzw. ν₂ besitzt. Eine Verschiebung des Meßtripelprismas hat aufgrund des Doppler-Effektes eine Frequenzverschiebung δν=2vν₂/c= 2v/λ₂ zur Folge, wobei v die Geschwindigkeit des bewegten Spiegels, c die Lichtgeschwindigkeit und λ₂ die zur Frequenz ν₂ gehörige Wellenlänge bezeichnen. Photoelektrisch werden die Signale mit der Zeitabhängigkeit cos(2π[ν₂-ν₁]t) und cos(2π(ν₂-ν₁±δν)t) aufgenommen und die Frequenzen in getrennten Zählern gezählt; anschließend wird mit jedem Referenzakt die vorzeichenrichtige Differenz gebildet. Die Summation der Differenzen ergibt dann die Wegstrecke in der Form:

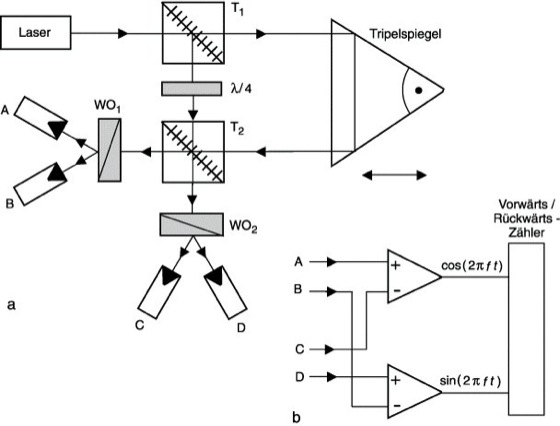
Interferenzlängenmessung 1: Michelson-Interferometer mit 4 um jeweils 90°
phasenverschobenen Ausgängen zur Längenmessung. a) Anordnung,
b) elektrische Signalverarbeitung.
A, B, C, D Photodetektoren,
WO_1,2 Wollaston-Prismen;
T₁, T₂ Strahlenteiler.

Interferenzlängenmessung 2: Heterodyninterferometer zur Längenmessung.
P₁, P₂ Polarisatoren;
D₁, D₂ Photodetektoren;
PST Polarisationsstrahlenteiler.