interferometrische Planflächenprüfung, die Bestimmung der Abweichungen von Planflächen von einer ebenen Bezugsebene mit Hilfe interferometrischer Verfahren. Meist wird das Fizeau-Interferometer benutzt, das die Summe der Abweichungen von Prüfling und Referenzfläche von der idealen Ebene zu messen erlaubt. Bei bekannten Absolutabweichungen einer Referenzfläche sind damit Kalibrierungen beliebiger Interferometerschaltungen möglich. Als ideal ebene Referenzflächen wurden Öl- und spezielle Quecksilberspiegel benutzt. Allerdings treten hierbei Stabilisierungsprobleme auf, die ihre Ursache in mechanischen Schwingungen, elektrostatischen Aufladungen, thermischen Störungen und Staub haben. Deshalb werden häufig Normalflächen als Referenzflächen vorgezogen, deren Abweichungen von der ideal ebenen Gestalt sich durch gegenseitigen Vergleich dreier solcher Flächen ermitteln lassen. Es werden also Zweierkombinationen der drei Flächen benötigt, um die Abweichungen ξ(x,y), η(x,y) und ζ(x,y) der drei Flächen von der Ebene zu erhalten. In einem Fizeau-Interferometer lassen sich die Summen ξ+η, ξ+ζ und η+ζ einzeln messen und damit η, ξ und ζ berechnen. Leider läßt sich dieses Verfahren nur auf Punkte anwenden, die auf einer Geraden liegen. Deshalb sind weitere Messungen erforderlich, bei denen die Platten um bestimmte Winkel gegeneinander verdreht werden.

Eine andere Methode der i. P., die besonders geeignet für technische Planflächen ist, besteht darin, daß man den Prüfling zum Bestandteil eines Interferometers macht, bei dem zwei identische Transmissionsgitter zur Strahlteilung und -vereinigung dienen (Abb.). Während bei ideal ebener Prüflingsoberfläche keine Interferenzerscheinungen zu beobachten sind, führen Abweichungen von der Ebenheit zum Auftreten von Interferenzkurven (ähnlich den Kurven gleicher Dicke).

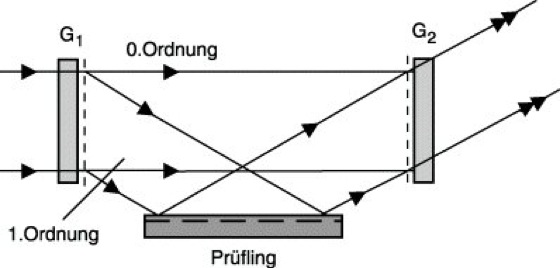
Interferometrische Planflächenprüfung: Prüfung technischer Oberflächen auf Ebenheit. G₁, G₂ identische Transmissions-Plangitter.