konische Refraktion, Bezeichnung für zwei Entartungsfälle der Lichtausbreitung in zweiachsigen Kristallen (Kristalloptik). Sie wurden 1832 von W. R. Hamilton berechnet und 1833 von H. Lloyd experimentell bestätigt.

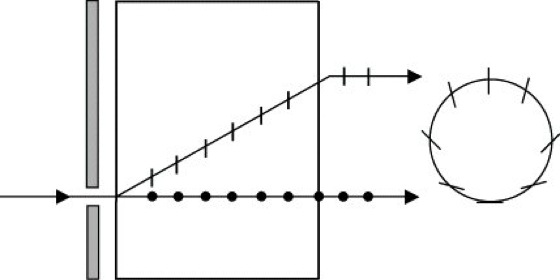
Äußere k. R. Ein senkrecht zur Biradialen geschnittener optisch zweiachsiger Kristall wird mit einem konvergenten Lichtbündel beleuchtet (Abb. 1), das auf eine Lochblende fällt (auf die aber auch verzichtet werden kann). Ihr genau gegenüber wird auf der Austrittsfläche des Kristalles eine zweite Lochblende angebracht. Dadurch wird ein Lichtstrahl (dünnes Bündel) ausgesondert, dessen Strahlrichtung mit der Binormalenrichtung zusammenfällt. Zu dieser ausgezeichneten Strahlrichtung gehören unendlich viele Wellennormalen, die auf einem Kegelmantel mit dem Öffnungswinkel ϕ_e liegen. Die Folge davon ist, daß der Strahl nach Austritt aus dem Kristalle im Außenraum (wo Normalenrichtung und Strahlrichtung identisch sind) in einen Kegelmantel auffächert (Abb. 1 und 2). Dessen Öffnungswinkel ist wegen der beim Austritt stattfindenden Brechung größer als ϕ_e. Letzterer ergibt sich aus der Beziehung

mit n_x, n_y, n_z als Hauptbrechungsindizes für den Fall n_z<n_y<n_x. Für rhombischen Schwefel gilt ϕ_e= 7°33'. Die austretenden Strahlen sind unterschiedlich linear polarisiert. Die in Abb. 1 eingezeichneten Polarisationsrichtungen gehen bei Wanderung entlang des Kegels stetig ineinander über.

Innere k. R. Ein schmales Strahlenbündel wird in einen senkrecht zur Binormalen geschnittenen optisch zweiachsigen Kristall eingestrahlt (Abb. 3). Zu der Wellennormale gehören in diesem speziellen Falle unendlich viele Strahlrichtungen im Kristalle, die auf einem Kegelmantel mit dem Öffnungswinkel ϕ_i liegen (Abb. 2). Es entsteht so innerhalb des Kristalles ein Kegel, dessen Mantel "Licht führt". Zwischen ϕ_i und ϕ_e besteht der Zusammenhang

.

Für rhombischen Schwefel hat ϕ_i den Wert 7°10,9'. Durch Brechung an der Austrittsfläche geht der Kegel in einen Kreiszylinder über, der auf einem Schirme einen Lichtring erzeugt. Die Polarisationsverhältnisse sind im oberen Teil von Abb. 2 dargestellt und entsprechen denen bei der äußeren k. R. Genauere Untersuchungen ergaben, daß der Lichtring der innern k. R. aus zwei Kreisringen besteht, die durch einen dunklen Ring voneinander getrennt sind (Poggendorfscher Kreisring). In ähnlicher Weise zerfällt der bei der äußeren k. R. auftretende Kegel in zwei Kegel.

Konische Refraktion 1: Äußere konische Refraktion.

Konische Refraktion 2: Äußere konische Refraktion: Zu der Strahlrichtung s, die mit der Richtung der Biradialen zusammenfällt, gehören in der gezeichneten Schnittebene die beiden Wellennormalen n₁ und n₂, die als die Normalen zu den Tangentialebenen t₁ und t₂ an die zweischalige Strahlenfläche S im Punkte U definiert sind. Außerhalb der Zwischenebene ergänzen sich n₁ und n₂ zum Kegel K₁ der äußeren konischen Refraktion. Innere konische Refraktion: Zu der Normalenrichtung n, die mit der Richtung der Binormalen zusammenfällt, gehören in der Schnittebene die beiden Strahlrichtungen s₁ und s₂. Diese sind dadurch definiert, daß ihre Verlängerungen die Strahlenflächen in den beiden Punkten treffen, in denen die zu n senkrechte Wellenfläche t₃ die Strahlenfläche als Tangentialebene gleichzeitig berührt. Die Strahlrichtungen s₁ und s₂ bilden räumlich ergänzt den Kegel K₂ der inneren konischen Refraktion.

Konische Refraktion 3: Innere konische Refraktion.