optische Abbildung, Erzeugung eines Bildes durch Umwandlung der vom abzubildenden Objekt ausgehenden Welle durch Brechung, Reflexion oder Beugung in einem optischen System in möglichst exakt konvergierende Wellen. Die o. A. thermischer Lichtquellen ist aufgrund der Addition der Intensitäten inkohärent; die o. A. beleuchteter Objekte erfolgt unter Interferenz der an diesen gebeugten, die Objektinformation tragenden Wellen mit dem ungebeugten Licht (Abb. 1e). Ist die Objektstruktur so klein, daß das gebeugte Licht vom optischen System nicht erfaßt wird, wird diese Struktur nicht abgebildet (Auflösungsvermögen). Da das Erfassen des am Objekt gebeugten Lichtes von der Beleuchtungsrichtung abhängt, ist die o. A. vom Verhältnis der Beleuchtungs- zur Abbildungsapertur (Kohärenzparameter) abhängig.

Geometrisch-optisch entspricht die o. A. der möglichst exakten Vereinigung der von den Dingpunkten ausgehenden homozentrischen Bündel in den Bildpunkten. Die o. A. ist reell, wenn sich die Strahlen direkt, virtuell, wenn sich nur ihre rückwärtigen Verlängerungen schneiden.

Die Beugung an der Aperturblende (Abb. 1d) und die Aberrationen (Abb. 1c) verhindern eine scharfe, punktuelle, ähnliche o. A. Eine scharfe o. A. eines räumlichen Objektes in eine Auffangebene ist wegen projektiver Unschärfe nur für die apertur- und empfängerabhängige Schärfentiefe möglich.

Die o. A. ist von der Brennweite des Abbildungssystems und vom Brennpunktsabstand des Abbildungsobjektes abhängig, die den Abbildungsmaßstab und die Bildlage bestimmen. Sammellinsen und Hohlspiegel bilden außerhalb der doppelten; zwischen doppelter und einfacher bzw. innerhalb der einfachen Brennweite liegende Objekte reell, umgekehrt und verkleinert; reell, umgekehrt und vergrößert bzw. virtuell, aufrecht und vergrößert ab (Abb. 2a). Die o. A. reeller Objekte durch Zerstreuungslinsen und Konvexspiegel ist immer virtuell, aufrecht und verkleinert (Abb. 2b) Linse, Spiegel.

Das einfachste Abbildungsmodell ist die Gaußsche Abbildung (Abb. 1a), bei der das Abbildungssystem durch Hauptebenen ersetzt wird. Als rein mathematische, nicht die physikalischen Gesetze der Lichtablenkung berücksichtigende, den gesamten Raum punktuell abbildende Transformation ist sie nur zur Beschreibung der paraxialen Abbildung geeignet. Optisch läßt sich der gesamte Raum punktuell nur mit der radialsymmetrischen inhomogenen Brechzahlverteilung des Maxwellschen Fischauges (Abb. 1b), allerdings verzerrt und mit chromatischer Aberration behaftet, abbilden. Die geometrisch-optische A. (Abb. 1c) berücksichtigt das Brechungsgesetz, den Malusschen Satz und die Dispersion. Sie setzt unendlich große Aperturen, d.h. keine Bündelbegrenzung durch beugende Blenden voraus. Da die Strahlablenkung an den Grenzflächen des Abbildungssystems erfolgt, existieren in der geometrischen Optik keine objektunabhängigen Hauptebenen. An Stelle des gesamten Raumes kann nur die achsenorthogonale Umgebung ausgewählter Objektpunkte punktuell abgebildet werden. Nur für diese aplanatische Abbildung lassen sich diesen konjugierten aplanatischen Punkten (O₁ und O

in Abb. 1c) konzentrische Hauptkugeln zuordnen. Alle übrigen Objektpunkte werden mit Aberrationen abgebildet. Die Hauptstrahlen legen in der geometrischen Optik die Bildgröße und damit den Abbildungsmaßstab fest. Das Modell der einfachen wellenoptischen A. berücksichtigt die Beugung an der Blende (Abb. 1d, Punktbildverwaschungsfunktion) und gilt nur für die Abbildung inkohärent beleuchteter Objekte. Das Modell der partiell kohärenten Abbildung (Abb. 1e) berücksichtigt den Beleuchtungseinfluß und die Beugung an der Objektstruktur und ist deshalb zur Beschreibung der Abbildung von Mikrostrukturen im μm-Bereich notwendig.

Nur auf der Beugung beruht die Abbildung durch Zonenplatten und Gitter einschließlich Hologramme.

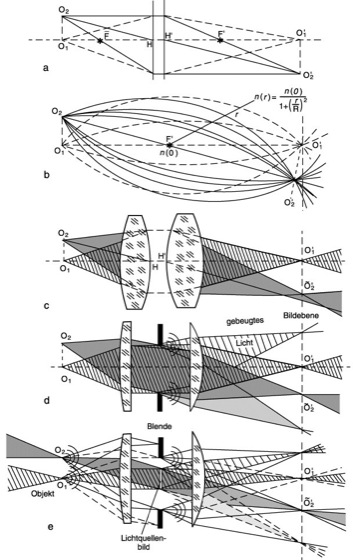
Optische Abbildung 1: Abbildungsmodelle. a) Gaußsche Abbildung, b) Abbildung beim Maxwellschen Fischauge, c) aplanatische Abbildung der geometrischen Optik, d) wellenoptische Abbildung unter Einfluß der Blendenbeugung, e) partiell kohärente Abbildung.

und F' Brennpunkte, H und H' Hauptpunkte, n Brechzahl.

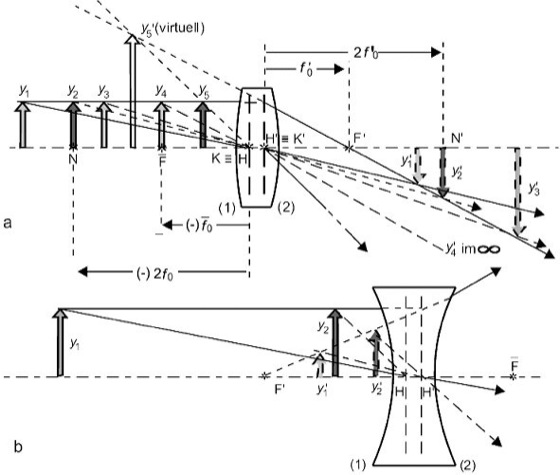
Optische Abbildung 2: optische Abbildung durch eine Sammellinse (a) und durch eine Zerstreuungslinse (b) bei Vernachlässigung der Aberrationen. H, H' Hauptpunkte; N, N' negative Hauptpunkte; K, K' Knotenpunkte;

, F' Brennpunkte;

₀, f'₀ Brennweiten.