optische Bildverarbeitung. Prinzipien der optischen Bildverarbeitung können immer dann sehr vorteilhaft zum Einsatz gebracht werden, wenn es darum geht, ganze Zeichenfelder bzw. Muster mit sehr großer Geschwindigkeit (in Echtzeit) parallel zu verarbeiten. Herkömmliche digital-elektronische Systeme dagegen müssen z.B. alle Positionen in einem Bild abtasten und die dabei erhaltenen Intensitätswerte seriell verknüpfen.

Diese Prozeduren sind zeitaufwendig und können das gegenwärtig für eine Auswertung anfallende Bildmaterial nicht in einer wirtschaftlich vertretbaren Zeit verarbeiten. Von besonderem Vorteil ist daher die Möglichkeit, optisch die Fourier-Transformation parallel und in Echtzeit ausführen zu können. Das geschieht mit Hilfe einer Linse in einer Anordnung gemäß Abb. 1. Nach der Kirchhoffschen Beugungstheorie führt eine Bildvorlage in Gestalt einer Transparenzverteilung g(x,y) in der Ebene E₁ in Fraunhoferscher Näherung zu folgender Lichterregung (beschrieben durch die komplexe Amplitude der elektrischen Feldstärke) in der Ebene E₂ mit den Koordinaten ξ, η


(1)

mit den Ortsfrequenzen p=ξ/λf und q=η/λf (λWellenlänge, f Brennweite der Linse), und (1) bedeutet gerade, daß G(p,q) die Fourier-Transformierte der Transparenzverteilung g(x,y) ist.

Alle bekannten Eigenschaften der linearen Fourier-Transformation können sehr vorteilhaft für eine o. B. genutzt werden. Besonders wichtig sind die folgenden:

Additivität:

Gilt für die Fourier-Transformierte von g₁ und g₂


. (2)

Verschiebung:


. (3)

Diese Beziehung bedeutet, daß eine Verschiebung in der Ortsebene in der Frequenzebene eine Phasenverschiebung zur Folge hat. Sie kann daher nur mit Hilfe eines phasenempfindlichen Empfängers registriert werden.

Ähnlichkeit:


. (4)

Einer Dehnung der Ortsfunktion in einer bestimmten Richtung entspricht also eine Stauchung der Frequenzfunktion in gleicher Richtung.

Drehung:

Wird die Ortsfunktion (z.B. eine Bildvorlage in Form einer Transparenzverteilung) um einen Winkel gedreht, dann dreht sich die Frequenzfunktion um den gleichen Winkel.

Produktzerlegbarkeit:

Kann die Ortsfunktion in ein Produkt von Funktionen zerlegt werden, die jeweils nur von einer der beiden unabhängigen Variablen abhängen, dann gilt für die Fourier-Transformierte


, (5)

wobei G₁, G₂ die Fourier-Transformierten von g₁ bzw. g₂ sind.

Faltung:

Läßt sich die Ortsfunktion in das Produkt zweier Funktionen zerlegen, dann erhalten wir die entsprechende Funktion im Frequenzbereich durch Faltung der jeweils einzeln transformierten Funktionen


(6)

Dabei gilt für die Faltung

Korrelation:


(7)

mit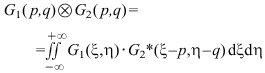

Differentiation:

Wird eine Funktion im Ortsbereich nach einer Variablen differenziert, dann entspricht das der Multiplikation der Fourier-Transformierten im Frequenzbereich mit einem frequenzproportionalen Faktor


. (8)

Bereits die Fourier-Transformation allein ist für die Erkennung bzw. Analyse von z.B. periodischen Strukturen sehr vorteilhaft anwendbar. In der Ebene E₂ der Abb. 1 befindet sich eine Detektormatrix, mit deren Hilfe das für eine spezielle Struktur charakteristische Fourier-Spektrum analysiert und einer elektronischen Weiterverarbeitung zugeführt wird. Infolge der optischen Vorverarbeitung, d.h. der Ausführung der Fourier-Transformation in Echtzeit, ist der für die weitere Informationsverarbeitung zu betreibende elektronische Aufwand geringer als ohne sie.

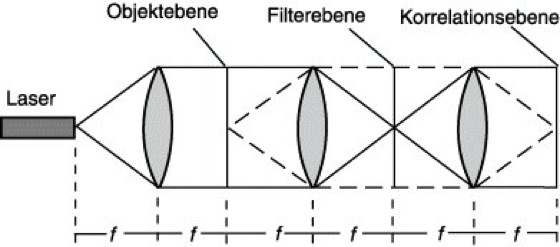
Ein weiteres Beispiel für die optische Bildverarbeitung ist die kohärent-optische Bildfilterung oder Zeichenerkennung (Abb. 2). Mit dieser Anordnung können Bildausschnitte oder auch Buchstaben z.B. innerhalb eines Textes erkannt werden.

Wenn z.B. innerhalb eines aufgezeichneten Textes der Buchstabe "S" oder innerhalb eines Bildes ein bestimmter Bildausschnitt wiedererkannt werden soll, dann muß von dem Buchstaben "S" bzw. dem Bildausschnitt ein Filter hergestellt werden. Als Filter kann das Fourier-Hologramm des Buchstabens "S" bzw. des Bildausschnittes b(x,y) benutzt werden. Zu dessen Herstellung wird von dem Buchstaben "S" bzw. dem Bildausschnitt b(x,y) ein Diapositiv erzeugt, davon wiederum wird mit Hilfe einer Fourier-Linse die Fourier-Transformierte gewonnen. Diese wird mit einer Referenzwelle mit der komplexen Amplitude R überlagert, so daß ein Hologramm entsteht (Holographie). Die Lichterregung in der Ebene E₂ (Abb. 1), die der Hologrammebene entspricht, ist durch


(9)

gegeben, wobei die Photoplatte die Intensität


(10)

registriert.

Die Hologrammplatte weist dann eine Transparenzverteilung auf, die zu I proportional ist


(11)

Das so hergestellte Filterhologramm ist in der in Abb. 2 gezeigten Anordnung in der Filterebene mit hoher Genauigkeit zu positionieren. In der Objektebene der Abb. 2 befindet sich das Diapositiv für ein beliebiges Eingangssignal v(x,y) mit F[v(x,y)]=V. In der Fourier-Ebene hinter dem Filterhologramm erhalten wir ein Signal in Gestalt der Lichterregung


(12)

wobei die beiden letzten Terme auf der rechten Seite von (12) die wesentlichen sind, sie repräsentieren die +1. und die -1. Beugungsordnung des Filterhologramms.

Die letzte Linse in Abb. 2 besorgt die Fourier-Transformation von (12), so daß für die Ausgangsfunktion A=F[S] gilt. Für die o. B. relevant ist der Anteil F[VB*R]=RF[VB*], der sich unter Verwendung von (7) zu

ergibt. Das hier auftretende Korrelationsintegral hat dann einen großen Wert – und führt damit zu einem sogenannten Korrelationspeak –, wenn die Bildvorlage (v) am Orte x, y und das Vergleichsbild (b) übereinstimmen. Wird daher beim vorgenannten Beispiel in die Objektebene ein Text gebracht, in dem der Buchstabe "S" vorkommt, dann erscheinen in der Korrelationsebene (Ausgangsebene) an den Stellen, an denen vor Einbringen des Filterhologramms der Buchstabe "S" zu sehen war, Korrelationspeaks (Intensitätsmaxima).

Dieses Verfahren ist jedoch technisch noch nicht ausgereift, so daß auch zu "S" sehr ähnliche Buchstaben mehr oder weniger intensive Korrelationspeaks hervorrufen. Nach dem eben beschriebenen Prinzip ist jedenfalls eine optische Vorverarbeitung von Informationen möglich, denn es werden alle Buchstaben eines Typs und auch die, die ihm ähnlich sind, in Echtzeit ausgewählt, so daß nach der kohärent-optischen Filterung eine Klasse relevanter Informationen vorliegt, die im Vergleich zur Ausgangssituation einen wesentlich geringeren Umfang besitzt. Eine nachfolgende elektronische Weiterverarbeitung der relevanten Klasse ist dann mit einem wesentlich geringeren Zeitaufwand möglich.

Soll ein Muster als eines aus einem Satz von N vorgegebenen Mustern erkannt werden, so muß nach dem eben beschriebenen Verfahren für jedes der möglichen Muster ein angepaßtes holographisches Filter hergestellt werden, und es müssen N analoge Messungen durchgeführt werden, um eine unbekannte Vorlage zu erkennen. Dieses Vorgehen erfordert eine große Anzahl sehr sorgfältiger Messungen. Die Zahl N der analogen Messungen läßt sich jedoch reduzieren, wenn die bekannte Tatsache genutzt wird, daß nur k "Ja"-"Nein"-Entscheidungen erforderlich sind, um aus N=2^k Vorlagen eine herauszufinden. Anstelle von 2^k Analogmessungen (Ermittlung von Korrelationen) brauchen daher nur k binäre Messungen ausgeführt zu werden. Zu diesem Zwecke werden die Vorlagen U_n(x,y)(n=1, 2, 3, ..., 2^k) mit k speziellen Filtern P_m(x,y)(m=1, 2, 3, ..., k) korreliert. Letztere werden so gewählt, daß die Korrelationswerte entweder "0" oder "1" sind, d.h., es müssen die Integrale ∫U_n(x,y)P*_m(x,y) dxdy entweder gleich 0 oder gleich 1 sein.

Den eben beschriebenen optischen Prozessorsystemen dürfen nur unverzerrte (im Vergleich zum ursprünglichen Zustand) Vorlagen angeboten werden, die Vorlagen dürfen auch nicht gegenüber ihrer ursprünglichen Lage gedreht werden, denn sonst würden sie nicht zu der Klasse der ausgewählten Vorlagen gehören. Damit von dem Prozessorsystem zunächst einmal auch verzerrte (im Maßstab geänderte) Vorlagen erkannt werden, wird die Filterherstellung modifiziert. Es wird nämlich die Transparenzverteilung g(x,y) der Muster einer Koordinatentransformation x=eξ, y=eη unterworfen, so daß wir g'(ξ,η) erhalten. Die Fourier-Transformierte der Funktion g'(ξ,η) entspricht der Mellin-Transformation, die skaleninvariant ist. Von der Funktion g'(ξ,η) wird ein synthetisches Fourier-Hologramm hergestellt und in die Filterebene der Anordnung in Abb. 2 gebracht. So aufgebaute optische Korrelatoren sind skaleninvariant.

Für den Aufbau eines skalen- und rotationsinvarianten optischen Korrelators wird aus dem absoluten Betrag G(p,q) der Fourier-Transformierten der Transparenzverteilung g(x,y) der Muster mittels einer Polarkoordinatentransformation die Funktion G'(r,ψ) erzeugt, wobei die Koordinatentransformation für r in der Form r=eρ fortgeführt wird. Es entsteht so die Funktion G″(ρ,ψ), von der ein Fourier-Hologramm hergestellt und in der Filterebene des optischen Prozessorsystems positioniert wird (Abb. 2).

Ein so aufgebautes optisches Prozessorsystem für die Korrelationsanalyse ist dann bewegungs-, skalen- und rotationsinvariant, d.h., die Vorlage kann bewegt, im Maßstab geändert und gedreht werden und wird dennoch als zu einer bestimmten Bildklasse gehörig erkannt.

Bilder müssen nicht unbedingt kohärent strahlen oder kohärent angestrahlt werden, wenn sie mit optischen Methoden erkannt bzw. verarbeitet werden sollen. Ein Anwendungsgebiet unter vielen anderen ist z.B. das Positionieren bzw. Sortieren von Werkstücken bei natürlicher oder künstlicher Beleuchtung. Diese Aufgabe kann folgendermaßen gelöst werden:

Das von dem zu erkennenden Objekt herrührende Licht O(x,y) ist nach dem obigen Verfahren mit Vergleichsmasken V_j(x,y) aller vorhandenen Objektklassen zu korrelieren, wobei alle möglichen Winkellagen in der Struktur der Vergleichsmaske zu berücksichtigen sind. Ein Maß für die Ähnlichkeit zwischen Objekt und Maske ist die Höhe des Korrelationspeaks, aus seiner Position in der Korrelationsebene kann auf die Lagekoordinaten des Objektes in der Objektebene geschlossen werden. Werden verschiedene Masken benutzt, dann können Objekte sortiert bzw. positioniert werden, auch Abstandsmessungen bzw. Winkelverdrehungen zwischen Objekt und Maske sind so meßbar.

Der Kontrast des Korrelationspeaks hängt stark vom Objekt und seinem Informationsgehalt ab. Strukturarme Objekte liefern sehr kontrastschwache Korrelationspeaks, um auch hier noch genau messen zu können, ist es notwendig, mit aufmodulierter Trägerfrequenz (Holographie) und Bandbreitenbegrenzung zur Rauschunterdrückung zu arbeiten. Zusätzliche Beleuchtung bzw. auf den Objekten angebrachte Strukturen erleichtern dem Korrelator die Erkennungsaufgaben.

In Hybridsystemen werden optische Prozessorsysteme mit Digitalrechnern verknüpft. Vom optischen Teil können dabei die numerisch sehr aufwendigen mathematischen Operationen (Fourier-Transformation, Faltung, Korrelation, ...) übernommen werden, während der Digitalrechner Steueraufgaben für bestimmte Bildausschnitte, Filter und Korrelationsmasken übernimmt.

Grundsätzlich handelt es sich bei der eben beschriebenen Technik um eine Analogtechnik, deren Arbeitsmedium die komplexe Amplitude des elektromagnetischen Wellenfeldes ist. Weiterhin wird die Tatsache genutzt, daß das elektromagnetische Wellenfeld in der Fourier-Ebene einer Linse auf die mannigfaltigste Art und Weise beeinflußt werden kann (durch Blenden, Modulatoren, Gitter, Transparenzverteilungen usw.).

Mit Hilfe optischer Prozessoren ist es unter Ausnutzung der eben geschilderten Eigenschaften möglich, mathematische Analogoperationen auszuführen sowie eine Bildvorverarbeitung vorzunehmen.

Schon allein die Tatsache, daß es mit Hilfe der beschriebenen optischen Prozessoren möglich ist, Klassen von Bildern oder Mustern auszuwählen, die später elektronisch oder vom Menschen weiterverarbeitet werden, ist von großem Vorteil. Ein solches Vorgehen wird eine bedeutende Entlastung der bisherigen digitalen Bildauswertetechnik zur Folge haben, weil bei der herkömmlichen Computerverarbeitung jedes einzelne Bild digitalisiert werden muß und da bei den zwar sehr genau arbeitenden digitalen Prozessoren die Verarbeitungszeit stärker als linear mit dem Informationsinhalt der Bilder wächst.

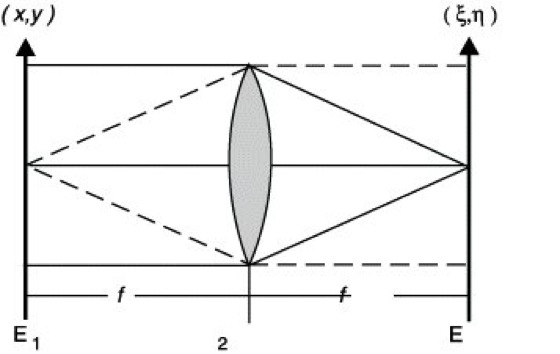
Optische Bildverarbeitung 1: Kohärent-optische Fourier-Transformation. Die Lichterregung in der Ebene E₂ ist die Fourier-Transformierte der Transparenzverteilung in der Ebene E₁. f Brennweite der Linse.

Optische Bildverarbeitung 2: Optisches Schema einer Anordnung zur kohärent-optischen Filterung. f Brennweite.