optische Nachrichtenübertragung, optische Nachrichtentechnik, die Übertragung von Informationen (z.B. Sprache, Musik, Bilder, Bewegtbilder oder Daten) mit Hilfe von elektromagnetischer Strahlung im optischen Frequenzbereich zwischen Sendern und Empfängern.

Bei der o. N. wird eine Nachricht als Signal einer Trägerwelle aufgeprägt. Mit steigender Frequenz der Trägerwelle wächst auch die verfügbare Übertragungsbandbreite. Bei konstant angenommenem Verhältnis zwischen der Leistung des Signals und der Leistung aller Störprozesse (Signal-Rausch-Verhältnis) steigt damit nach dem Shannon-Theorem auch die Übertragungskapazität (d.h. die in einem gegebenen Zeitraum übertragbare Informationsmenge).

Die Wahl der Trägerfrequenz hängt einerseits von den nachrichtentechnischen Anforderungen wie Übertragungskapazität, Übertragungsstrecke, zulässige Fehlerrate und Signalverzögerung, andererseits aber auch von den Parametern der erforderlichen Sende- und Empfangskomponenten und den Eigenschaften des Übertragungskanals ab.

Meist wird zur quantitativen Bewertung eines optischen Nachrichtenübertragungssystems das Bandbreiten-Reichweite-Produkt (in MHz·km oder auch Mbit/s·km für digitale Systeme) verwendet. Diese Größe wurde deswegen gewählt, weil die Mehrzahl der kapazitätsbegrenzenden Einflüsse proportional zur Länge der Übertragungsstrecke ist.

Ein System zur o. N. besteht aus folgenden Komponenten:

- Die elektrische Signalquelle, welche die (digitalen oder analogen) Nachrichten abgibt.

- Die optische Quelle.

- Der Modulator. Dabei kann entweder direkt die optische Quelle in einer oder mehreren Eigenschaften moduliert werden, oder aber das Signal wird nachträglich dem Licht aufgeprägt.

- Der Übertragungskanal, dessen Eigenschaften im wesentlichen von der Wahl des Übertragungsmediums abhängen.

- Innerhalb des Übertragungskanals können sich weitere optische oder optisch-elektrische Komponenten wie z.B. Filter, Verstärker oder Regeneratoren befinden.

- Der Empfänger, der das eintreffende Licht wieder in ein elektrisches Signal umwandelt.

- Falls nötig wird die Information über einen Demodulator im optischen und/oder im elektrischen Teil des Empfängers in ihre ursprüngliche Form zurückverwandelt.

- Die Signalsenke, die die empfangene Nachricht verarbeitet.

- Bei digitalen Systemen ist in der Regel ein Taktsystem zur Synchronisation der Komponenten erforderlich. Die Taktinformation der Quelle kann entweder über den Kanal mit übertragen oder aus dem empfangenen Nachrichtensignal zurückgewonnen werden (Taktrückgewinnung).

Bei der o. N. unterscheidet man zwischen der Freiraumübertragung, bei der sich das Licht in der Atmosphäre oder auch im Weltraum ausbreitet, und der Lichtleiternachrichtenübertragung, bei der das Licht in einem eigens dafür geschaffenen Lichtleiter geführt wird.

1) Freiraumübertragung. Hierbei nimmt die Leistung pro Flächeneinheit mit dem Quadrat der Entfernung zwischen Quelle und Empfänger ab. Bei einer ungerichteten Verbindung, bei der die Quelle in den gesamten Raum, oder mindestens in einen beträchtlichen Teil davon, abstrahlt und der Empfänger Licht aus dem gesamten Raum, oder mindestens aus einem beträchtlichen Teil davon, empfängt, sind die mögliche Übertragungskapazität und die Reichweite stark begrenzt. Das theoretisch erzielbare Bandbreiten-Reichweite-Produkt für Systeme in Räumen mit Sonneneinstrahlung bei Wellenlängen in nahen Infrarot (z.B. bei 800 nm) liegt bei nur einigen 100 MHz m. Dennoch werden solche Systeme technisch vielfältig eingesetzt. Praktisch in jedem Haushalt finden sich mehrere Infrarot-Fernbedienungen, die einige kBit/s über einige Meter übertragen. Auch die drahtlose Verbindung von Rechnerkomponenten durch teilgerichtete optische Verbindungen mit Datenraten von einigen Mbit/s über einige Meter findet zunehmende Verbreitung.

Für größere Entfernungen werden gerichtete Verbindungen verwendet. Die Divergenz der von der Quelle ausgesandten und der vom Empfänger aufgenommenen Strahlung wird dabei gegebenenfalls mit Hilfe abbildender optischer Elemente wie Linsen oder Spiegel verringert. Eine geringe Divergenz des Senders erhöht die Lichtleistung am Empfänger. Eine kleine Divergenz des Empfängers verringert den Anteil des empfangenen Umgebungslichtes und damit die Störungen. Je kleiner die Divergenz ist, um so höher ist allerdings die erforderliche Genauigkeit der Ausrichtung von Sender und Empfänger zueinander.

Die durch die reine Ausbreitung bedingten Strahlungsverluste werden als Freiraumverluste bezeichnet. Bei Ausbreitung in der Erdatmosphäre kommen Absorptions- und Streuverluste hinzu.

Eine verbreitete Anwendung von Freiraumverbindungen ist die zeitweilige Herstellung von Telekommunikations- oder Datenverbindungen über Strecken von einigen Kilometern, z.B. für Baustellen. Sehr erfolgversprechend ist die Kommunikation von Satelliten untereinander mit optischen Systemen. Dank der geringeren Wellenlänge im Vergleich zu herkömmlichen Funkverbindungen kann eine größere Übertragungskapazität erzielt werden. Probleme der Strahlsuche, -nachführung und der Kompensation des Doppler-Effekts müssen noch gelöst werden.

2) Lichtleiternachrichtenübertragung. Umgibt man ein optisches Medium mit dem Brechungsindex n mit einem Material kleineren Brechungsindexes, werden alle Strahlen vollständig reflektiert, die die Grenzfläche unter einem Winkel erreichen, der kleiner ist als der Grenzwinkel der Totalreflexion. Alle Lichtstrahlen, die innerhalb dieses Winkelbereiches liegen, werden daher im Material mit dem dichterem Medium, dem Kern, geführt. Bei Krümmungen des Kerns mit Radien, die weit oberhalb der Abmessungen des Kerns liegen, bleibt die Lichtführung erhalten. Ein Wellenleiter kann als eine planare (ebene) Struktur auf verschiedenen Materialien wie z.B. Glas, LiNbO₃ oder InP ausgebildet werden. Das ermöglicht die Gestaltung von optisch integrierten Schaltungen.

Von besonderer Bedeutung für die o. N. ist die seit den 60er Jahren technisch realisierte Herstellung von optischen Fasern. Dabei wird zunächst eine Vorform hergestellt, die bereits das Brechungsindexprofil (Abhängigkeit des Brechungsindexes vom Abstand zur Achse der runden Faser) der späteren Faser aufweist. Durch Ziehen wird daraus die Faser gewonnen. Das am häufigsten verwendete Material für optische Fasern ist Quarzglas. Für kurze Entfernungen werden auch Lichtwellenleiter aus PMMA (Polymethylmethacrylat) verwendet.

Die Faser besteht aus einem Kern mit dem Durchmesser d von der Größenordnung der Lichtwellenlänge λ und einem Mantel. Im Kern fällt der Brechungsindex von einem Wert n₁ auf der Faserachse nach außen entweder stufenförmig oder stetig nach einem Potenzgesetz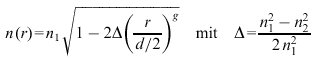

und r als Abstand von der Faserachse auf den Wert n₂ des Mantels ab. Häufig werden Werte des Profilparameters g nahe 2 realisiert. Ein stufenförmiger Brechungsindexverlauf entspricht dem Limes g→∞.

Je nachdem, welche Art des Brechungsindexprofils vorliegt, spricht man von Stufenindex- oder Gradientenindexfasern.

In den ersteren erfolgt eine Führung der Lichtwellen infolge Totalreflexion an der Grenzfläche zwischen Kern und Mantel. Die einzelnen Lichtstrahlen breiten sich daher zickzackförmig aus. Bei Gradientenindexfasern beschreiben sie gekrümmte Bahnen, die ebenfalls immer wieder ins Faserinnere zurückführen (Abb. 1). Die Randbedingungen haben zur Folge, daß sich in der Faser nur diskrete Wellenformen, die sogenannten Moden, ausbilden können. Eine solche Mode wird dabei von der Gesamtheit aller Strahlen gebildet, die von der Faserachse unter einem bestimmten Winkel starten. Die Randbedingungen lassen jedoch nur diskrete Winkelwerte zu.

Der maximale Akzeptanzwinkel α_max einer Stufenindexfaser ist gegeben durch

Diese Größe kennzeichnet die numerische Apertur NA. Sie liegt typischerweise bei 0,2. Bei Gradientenindexfasern gilt die angegebene Beziehung nur für Strahlen, die in der Mitte der Faser eintreten. Tun sie dies in einem Abstand r, so ist r₁ durch n(r) zu ersetzen. Man spricht dann von einer lokalen numerischen Apertur, die mit wachsendem r offenbar immer kleiner wird.

Für die Zahl der Moden in einer optischen Faser gilt allgemein

Bei Verringerung der Dicke d des Faserkerns ist eine Lichtausbreitung schließlich nur noch in Richtung der Faserachse möglich. Man gelangt so zu einer Einmodenfaser, im Unterschied zu den oben betrachteten Mehrmodenfasern. Einmodenfasern können sowohl als Stufen- als auch als Gradientenindexfasern ausgebildet sein.

3) Dämpfung in optischen Medien. Neben der oben erwähnten Freiraumdämpfung wird das Licht bei der Ausbreitung durch verschiedene Mechanismen wie Absorption oder Streuung geschwächt. Dabei nimmt die Intensität in den meisten Fällen exponentiell ab, so daß ein Dämpfungskoeffizient α definiert werden kann. Die ursprüngliche Intensität I₀ verringert sich dann nach einer Strecke L auf I=I₀exp(-αL).

Die Dämpfung der optischen Strahlung wird in dB/km (Dezibel pro Kilometer) angegeben. Wenn auf einer Strecke von 1 km eine Dämpfung um den Faktor 10^x/10 erfolgt, so beträgt diese xdB.

Man unterscheidet lineare und nichtlineare Dämpfungsprozesse. Bei den ersteren ist der Dämpfungskoeffizient unabhängig von der momentanen Lichtintensität, bei den letzteren hängt er davon ab.

Nachfolgend werden Dämpfungsursachen bei der Freiraumübertragung in Luft und bei der Lichtleiternachrichtenübertragung in Quarzglasfasern zusammengestellt.

Bei Freiraumübertragung in Luft spielt die Absorption an H₂O, CO₂ und O₃ (mit geringsten Dämpfungen in einem Wellenlängenbereich zwischen 0,4 und 1,3 μm sowie zwischen 10 und 12 μm) sowie an Hindernissen im Strahlweg (Bäume, Vögel) eine Rolle.

Rayleigh- bzw. Mie-Streuung tritt an Molekülen, Rauch- und Staubteilchen, Dunst, Nebel, Regen oder Schnee auf. Dazu kommt Streuung an Brechzahlschwankungen infolge von Luftturbulenzen und Temperaturdifferenzen sowie an Hindernissen im Lichtweg.

Bei Quarzglasfasern dominiert die Absorptionsbande der Si-Atome bei ca. 10 μm die Verluste oberhalb 1,6 μm. Als Folge geringster Anteile von OH^--Ionen im Quarzglas treten Absorptionsbanden z.B. bei 1,4 μm auf. Rayleigh-Streuung wird durch Inhomogenitäten mit Abmessungen weit unterhalb der Lichtwellenlänge λ hervorgerufen. Die Verluste sinken dabei proportional zu λ^-4. In der Quarzglasfaser dominiert sie die Dämpfung unterhalb 1,5 μm. Mie-Streuung entsteht an Inhomogenitäten mit Abmessungen im Bereich der Lichtwellenlänge oder größer. Beide Streuprozesse sind aufgrund der unregelmäßigen atomaren Struktur des Glases unvermeidlich. Zusätzliche Verluste treten durch Änderungen von Faserkerndurchmesser, -exzentrizität oder Brechungsindex mit der Länge auf. Störend wirken sich auch mechanische Belastungen und Faserkrümmungen aus.

In der Glasfaser müssen auch nichtlineare Effekte berücksichtigt werden. Die stimulierte Raman- und die stimulierte Brilloin-Streuung sind bei schmalbandigen Quellen und bei Leistungen oberhalb ca. 1 mW relevant. Dabei wird ein Teil des Lichtes (mit geänderter Frequenz) zurück oder in Ausbreitungsrichtung gestreut. Die Intensitätsabhängigkeit des Brechungsindexes führt bei starken Impulsen zu einer Erhöhung des Brechungsindexes im Verlauf der ansteigenden Flanke. Bei günstiger Wahl der Parameter verringert dies die Impulslänge. Ein weiterer nichtlinearer Effekt ist die Vierwellenmischung. Bei Übertragung von Licht mehrerer Wellenlängen in einer Faser kommt es dadurch zum Energieaustausch zwischen den Teilwellen. Für Systeme mit Wellenlängenmultiplex kann dieser Effekt zur dominierenden Störung werden. In Abb. 2 sind die wellenlängenabhängigen Verluste in verschiedenen Quarzglas- und Polymerfasern dargestellt. Tab. 1 zeigt einige typische Parameter heute eingesetzter optischer Fasern.

4) Dispersion in optischen Fasern. Jedes optische Signal besitzt, entweder durch die Eigenschaften der Quelle vorgegeben oder aber durch die Modulation hervorgerufen, eine spektrale Breite. In einer Faser treten daher Dispersionseffekte auf. Man spricht von chromatischer Dispersion – im Unterschied zu der unten erwähnten Modendispersion –, wenn die Ausbreitungsgeschwindigkeit des Lichtes wellenlängenabhängig ist. Nach Durchlaufen einer Strecke sind dann die monochromatischen Anteile eines Lichtimpulses gegeneinander verzögert (man mißt die chromatische Dispersion daher in der Einheit ps/nm·km), was zu einer Verbreiterung des Impulses führt. Die chromatische Dispersion ist sowohl durch die Wellenlängenabhängigkeit des Brechungsindexes des Fasermaterials (Materialdispersion) als auch durch die Wellenleitereigenschaften (Wellenleiterdispersion) bedingt. Die Wellenleiterdispersion wird bei Einmodenfasern im wesentlichen dadurch hervorgerufen, daß sich die Feldverteilung im Faserkern und im angrenzenden Mantel mit der Wellenlänge ändert.

Durch geeignete Wahl der Indexprofils kann die chromatische Dispersion in Einmodenfasern variiert werden. Die üblicherweise verwendete Faser hat eine verschwindende Dispersion bei einer Wellenlänge von ca. 1,3 μm. Die dispersionsverschobene Einmodenfaser zeigt ein Minimum bei 1,55 μm, das in den Arbeitsbereich von erbiumdotierten Faserverstärkern (s.u.) fällt. Bei dispersionsgeglätteten Einmodenfasern ist die Dispersion sowohl bei 1,3 μm als auch bei 1,55 μm sehr klein. Mit dispersionskompensierenden Einmodenfasern kann die chromatische Dispersion einer Faser nachträglich ausgeglichen werden, da ihre Dispersion den vielfachen Wert der Standardfaser aufweist (bei umgekehrtem Vorzeichen). In Abb. 3 werden typische Werte für die chromatische Dispersion unterschiedlicher Einmodenfasern einander gegenübergestellt. Von besonderem Interesse sind die Werte an den üblichen Arbeitspunkten um 1300 nm und 1550 nm. Bei Mehrmodenfasern haben die unterschiedlichen Moden (bei fester Wellenlänge) verschiedene Ausbreitungsgeschwindigkeiten. Dieser Effekt wird als Modendispersion bezeichnet. Er ist bei Stufenprofilfasern erheblich größer als bei Gradientenprofilfasern. Durch geeignete Wahl des Profilparameters kann die Summe von Moden- und chromatischer Dispersion minimiert werden.

In Lichtwellenleitern ist in der Regel Licht zweier Polaristionsrichtungen ausbreitungsfähig. Unterscheiden sich die zugehörigen Ausbreitungskonstanten, kommt es zur Polarisationsmodendispersion. Wegen der statistisch schwankenden Doppelbrechung in Glasfasern wächst hier die Impulsverbreiterung mit der Wurzel aus der Entfernung. Die Polarisationsmodendispersion wurde experimentell zu etwa

bestimmt. Sie spielt damit nur für extrem hochbitratige Systeme bei großen Entfernungen eine Rolle.

Bei Stufenindexfasern bestimmt die Modendispersion in den meisten Fällen die Kapazität des Systems. Diese Fasern sind deswegen für mittlere Datenraten und kleine Entfernungen anwendbar. Die chromatische Dispersion kann bei hochbitratigen Systemen der begrenzende Faktor werden, insbesondere wenn man wegen der Verfügbarkeit von erbiumdotierten Faserverstärkern bei 1,5 μm arbeiten will. Dispersionskompensierende Maßnahmen versprechen hier weitere Leistungsverbesserungen.

5) Quellen für optische Systeme. Diese müssen, je nach Anwendungsfall, unterschiedlichen Anforderungen genügen. Für Freiraumübertragungssysteme sind vor allem wichtig: hohe Ausgangsleistung, Wellenlänge im Bereich geringer atmosphärischer Dämpfungen (z.B. bei 10,6 μm), geringe Strahldivergenz für gerichtete Systeme und große Bandbreite, falls die Quelle direkt moduliert wird.

Für Lichtleiternachrichtenübertragungssysteme sind von Bedeutung: Ausgangsleistungen im Bereich einiger mW, Wellenlängen im Bereich der kleinsten Faserdämpfungen (0,85 μm, 1,3 μm oder 1,55 μm für Quarzglas- bzw. 0,65 μm für PMMA-Polymerfasern), Anpassung von strahlender Fläche und Divergenz der Strahlung an die Parameter der verwendeten Faser, große Modulationsbandbreite für den Fall direkter Modulation und geringe spektrale Breite der unmodulierten Strahlung zwecks Reduzierung des Einflusses der Dispersion.

Diese Anforderungen werden in hervorragender Weise von Lasern erfüllt. Verschiedene Gaslaser oder Festkörperlaser werden für Freiraumübertragungssysteme verwendet. Für Lichtleiternachrichtensysteme werden heute praktisch nur noch Halbleiter-Laserdioden (LD) und Lumineszenzdioden (LED) eingesetzt.

6) Modulation des Lichtes. Um analoge oder digitale Signale mit Hilfe von Licht zu übertragen muß die Nachricht diesem Licht aufgeprägt werden (Modulation).

Bei inkohärentem Licht, wie es z.B. von einer LED emittiert wird, kann nur die Lichtleistung (Intensität) moduliert werden. Bei Halbleiterdioden kann die optische Leistung direkt über den Strom gesteuert werden. Zur Erzeugung digitaler Binärsignale wird üblicherweise die Quelle im Takt der Bits ein- und ausgeschaltet. Analoge Signale können nur übertragen werden, wenn die Kennlinie der Diode (Lichtleistung in Abhängigkeit vom Strom) über einen größeren Bereich hinreichend linear ist.

Es ist ebenso möglich, die Lichtleistung nachträglich zu verändern (externe Modulation), indem z.B. die Dämpfung eines nachgeschalteten Bauelementes moduliert wird. Bei kohärenten Quellen (Lasern) kann neben der Intensität auch Frequenz, Phase oder Polarisation verändert werden. Das wird insbesondere beim Überlagerungsempfang ausgenutzt. Im Falle von binären Signalen werden den Symbolen "0" und "1" unterschiedliche Werte der Intensität, der Frequenz, der Phase oder der Polarisation zugeordnet. Man unterscheidet entsprechend Amplituden-, Frequenz-, Phasen- und Polarisationsumtastung. Für analoge Modulation kommen nur Amplituden- oder Frequenzmodulation (vergleichbar dem UKW-Prinzip) in Frage.

Auch Frequenz, Phase oder Polarisation können mit Hilfe externer Bauelemente moduliert werden. Am verbreitetsten sind die Frequenzmodulation direkt über den Laserstrom (die Emissionsfrequenz von Laserdioden verschiebt sich typischerweise um 10 GHz bei 1 mA Stromänderung) und die Modulation der Phase mit externen Bauteilen. Dazu wird in einem wenige mm langen Wellenleiter durch ein angelegtes elektrisches Feld der Brechungsindex so variiert, daß sich die optische Länge um z.B. λ/2 ändert. Für Freiraumübertragung in der Atmosphäre kommt, bedingt durch Phasenfluktuationen aufgrund von Luftdichteschwankungen, praktisch nur Intensitätsmodulation in Frage. Für Weltraumanwendungen sind alle beschriebenen Modulationsverfahren diskutiert worden.

7) Empfänger für optische Übertragungssysteme. Die einzigen Empfänger für optische Übertragungssysteme von nennenswerter praktischer Bedeutung sind Photodioden. Die zwei wichtigsten Typen sind die pin- und die Avalanche-Photodiode (Tab. 2).

8) Optische Verstärker und Regeneratoren. Reicht die Reichweite eines optischen Systems nicht aus, können auf dem optischen Kanal (Lichtleiter) Zwischenverstärker eingesetzt werden.

Bei einem Regenerator wird das optische Signal einer Photodiode in ein elektrisches Signal umgewandelt, elektrisch verstärkt und anschließend wieder einem optischen Träger aufmoduliert. Zusätzlich ist eine Rekonstruktion der Impulsform möglich, wodurch das Signal-Rausch-Verhältnis verbessert wird, sowie eine Wiederherstellung der exakten Impulsposition (Verringerung des Jitters). In diesem Fall spricht man von 3R-Regeneration.

Mit Hilfe optischer Verstärker kann das Signal direkt verstärkt werden. Dazu können Halbleiterverstärker (SOA, Abk. für engl. Semiconductor Optical Amplifier) oder Verstärker auf der Basis erbiumdotierter Fasern (EDFA, Abk. für engl. Erbium Doped Fiber Amplifier) verwendet werden (Abb. 4). Während erstere für alle Wellenlängenbereiche hergestellt werden können, für die auch Laserdioden realisierbar sind, verstärken EDFA nur in einem Bereich von etwa 1530 bis 1560 nm. Mit noch nicht praxistauglichen Verstärkern auf der Basis von praseodymdotierten Fasern ist auch Verstärkung bei 1,3 μm erzielt worden.

Optische Verstärker erhöhen nur die Signalamplitude. Das Signal-Rausch-Verhältnis und die Genauigkeit der Impulsposition verschlechtern sich kontinuierlich entlang der Strecke. Unter Ausnutzung nichtlinearer Effekte ist bei Solitonen-Übertragungssystemen eine rein optische Nachrichtenübertragung über im Prinzip unbegrenzte Entfernungen möglich (Soliton).

9) Design optischer Übertragungssysteme. Heute existieren eine sehr große Zahl verschiedener Architekturen von optischen Übertragungssystemen. Neben den Parametern der Quellen, der Empfänger, des verwendeten Mediums und weiterer Elemente müssen auch Fragen der Installation und Wartung, ökonomische und rechtliche Probleme sowie Lebensdauer und Ausbaufähigkeit des Systems betrachtet werden. An dieser Stelle sollen beispielhaft einige typische Anwendungsfälle beschrieben werden.

Heutige Telekommunikationsnetze sind zumindest im Fernnetz komplett digital aufgebaut. Die derzeit verwendete Technik ist die sogenannte Synchrone Digitale Hierarchie (SDH). Es werden Datenraten zwischen 155 Mbit/s und 2,5 Gbit/s realisiert. Die Daten werden dabei zu Blöcken zusammengefaßt. Die verschiedenen Bitraten sind so gewählt, daß mehrere Datenströme einer niedrigeren Stufe in einen Datenstrom der höheren Kategorie zusammengefaßt werden können (z.B. 4-mal 155 Mbit/s in einmal 622 Mbit/s). Üblicherweise werden Laserdioden bei 1,55 μm als direkt modulierte Quellen benutzt. Für die in Entwicklung befindlichen Systeme mit 10 Gbit/s und mehr werden externe Modulatoren vorgesehen. Zur Vergrößerung der Reichweite werden sowohl Regeneratoren, als auch in zunehmendem Maße EDFA-Verstärker eingesetzt.

Für interkontinentale Verbindungen werden Unterseekabel mit Übertragungslängen bis zu 10000 km verwendet. Die größte Kapazität haben dabei Solitonensysteme. Hier wird die Tatsache ausgenutzt, daß bei bestimmten Signalpegeln die nichtlinearen Effekte in der Faser die Dispersion kompensieren können. Längs einer Übertragungsstrecke werden dabei bis zu mehreren Hundert kaskadierter EDFA-Verstärker benötigt. Die Übertragungskapazität erreicht viele Gbit/s. Solitonensysteme mit Raman-Faserverstärkern spielen dagegen keine praktische Rolle.

Beim Überlagerungsempfang wird das von einem Sendelaser eintreffende Licht im Empfänger mit dem Licht eines zweiten Lasers (Lokaloszillator) gemischt. Dessen Frequenz kann genau der Frequenz des Sendelasers entsprechen, oder aber davon um Werte bis zu einigen GHz abweichen. Aufgrund der quadratischen Kennlinie der Photodiode entsteht ein elektrisches Signal, das dem Phasen- und Amplitudenverlauf des Sendesignals entspricht (optischer Überlagerungsempfang).

Am Heinrich-Hertz-Institut Berlin wurde der erste vollständig integrierte Überlagerungsempfänger realisiert. Wegen des großen Aufwandes konnten sich Überlagerungssysteme im praktischen Betrieb nicht durchsetzen, obwohl sie die höchste Empfindlichkeit und optimale Ausnutzung der optischen Bandbreite erlauben. Den prinzipiellen Aufbau eines Überlagerungssystems zeigt Abb. 5.

Die Zukunftsvision der o. N. ist das sogenannte transparente optische Netz. Dabei werden die großen Vermittlungsstellen über ein voll vermaschtes Glasfasernetz verbunden. In jeder Faser kann sich Licht bei vielen Wellenlängen gleichzeitig ausbreiten. An den Vermittlungsstellen befinden sich optische Cross-connects, d.h. Schalteinrichtungen, die die Signale von den eingehenden Fasern beliebig auf die abgehenden Fasern umschalten können, wobei auch der Wellenlängenkanal gewechselt wird. An Add-Drop-Multiplexern können einzelne Kanäle eingefügt oder entnommen werden. Alle diese Prozesse erfolgen rein optisch ohne elektrische Signalverarbeitung. Bei typischen Ausdehnungen des Netzes von 1000 km sind viele Kanäle mit jeweils bis zu 10 Gbit/s denkbar. Viele Probleme, insbesondere solche der Verwaltung eines derartigen Netzes, müssen noch gelöst werden.

Optische Nachrichtenübertragung 1: Brechungsindexverlauf und typischer Strahlverlauf in verschiedenen Lichtleitfasern. a) Mehrmodenfaser mit Stufenprofil. Es bilden sich typischerweise mehrere 100 Moden aus. Gebräuchliche Durchmesser sind 100 μm für den Kern und 140 μm für den Mantel. b) Mehrmodenfaser mit Indexprofil. Die Modenzahl liegt auch hier typischerweise bei mehreren 100 Moden. Gebräuchliche Durchmesser sind 62,5 μm für den Kern und 125 μm für den Mantel. c) Einmodenfaser. Das eingestrahlte Licht breitet sich nur in Richtung der Kernachse aus. Gebräuchliche Durchmesser sind 10 μm für den Kern und 125 μm für den Mantel.

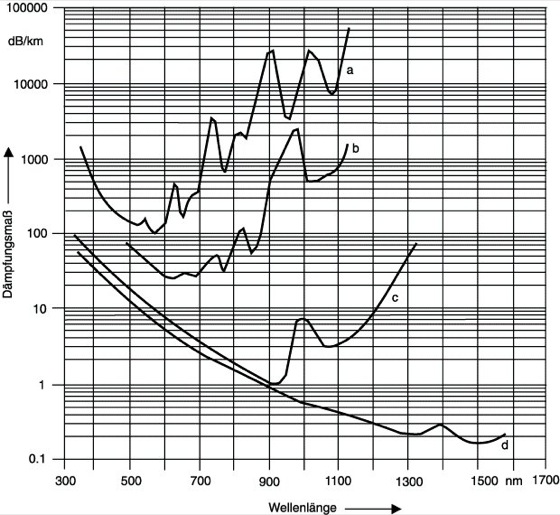
Optische Nachrichtenübertragung 2: Abhängigkeit des Dämpfungsmaßes verschiedener optischer Fasern von der Wellenlänge. a) Polymerfaser auf der Basis von PMMA, b) Polymerfaser auf der Basis von deuteriertem PMMA (Austausch aller H-Atome gegen Deuterium), c) Quarzglas-Mehrmodenfaser mit Kunststoffmantel, d) Quarzglas-Einmodenfaser.

Optische Nachrichtenübertragung 3: Chromatische Dispersion in typischen Fasern. a) Standard-Einmodenfaser, b) dispersionsverschobene Einmodenfaser, c) dispersionsgeglättete Einmodenfaser.

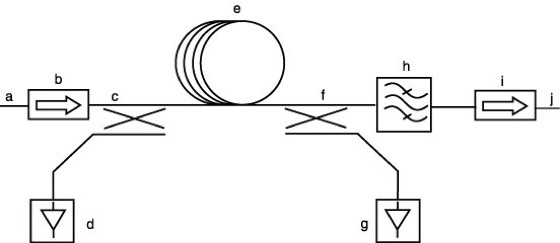
Optische Nachrichtenübertragung 4: Aufbau eines EDFA-Faserverstärkers. Das zu verstärkende Signal wird in den Eingang a eingekoppelt. Über den Koppler c wird vom Laser d Pumplicht hinzugefügt. Dabei können Wellenlängen von 980 oder 1400 nm verwendet werden. Die Faser e ist mit Erbium dotiert. Die Erbiumatome werden durch das Pumplicht angeregt. Ein optisches Signal im Wellenlängenbereich um 1550 nm wird durch induzierte Emission verstärkt. Das Pumpen kann entweder in Richtung des Signalflusses, entgegen dessen Richtung (hier mit Hilfe des Lasers g und des Kopplers f) oder auch in beiden Richtungen gleichzeitig erfolgen.
Störungen durch Reflexionen werden mit Hilfe von Faraday-Isolatoren b und i verringert. Ein großer Teil der im Faserverstärker entstehenden spontan emittierten Lichtleistung kann durch ein zusätzliches Bandpaßfilter h unterdrückt werden. Den Ausgang j verläßt dann nur noch das verstärkte Signal.

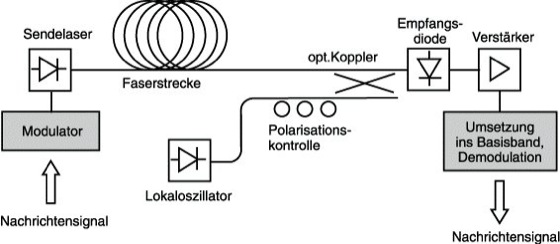
Optische Nachrichtenübertragung 5: Schematische Darstellung eines Systems mit Überlagerungsempfang.