optische Übertragungsfunktion, zur Beschreibung der Abbildungs- bzw. Wiedergabequalität von optischen Abbildungs- und Bildaufzeichnungssystemen (optische Systeme, photographische Schichten, CCD-Empfänger, Streuscheiben) sowie der Güte der Bildübertragung beim Fernsehen verwendete Gütefunktion.

1) Grundlagen. Die Eigenschaften des Übertragungssystems zeigen sich am deutlichsten bei gitterförmigen Strukturen, d.h. bei Objekten mit einer sinusförmig modulierten Intensitätsverteilung


. (1)

Hierbei bedeuten

die mittlere Intensität, I₁ die Amplitude des Sinusanteils der Intensität, R den als Ortsfrequenz bezeichneten Kehrwert der Gitterkonstanten g und ϑ die – durch das Verhältnis der Verschiebung x_ϑ des Gitters bezüglich des Koordinatenursprungs zur Gitterkonstanten gegebene – Phasenlage. Durch die Übertragung wird die Intensitätsverteilung (1) des Objektes in eine ebenfalls sinusförmig modulierte Intensitätsverteilung


(2)

in der Bildebene überführt (Abb. 1). Dabei ändert sich zunächst die Gitterkonstante bzw. die Ortsfrequenz, und zwar gilt im Falle eines abbildenden Systems mit dem Abbildungsmaßstab β' die Beziehung R'=R/β'. Für die Qualität der Abbildung entscheidend sind jedoch die Änderungen einerseits des Modulationsgrades m, auch Modulation genannt, worunter man den Kontrast


(3)

der Intensitätsverteilung versteht, und andererseits der Phasenlage. Diese Änderungen kann man in der Form


, (4)


(5)

schreiben, wobei es zweckmäßig ist, alle Größen auf die Ortsfrequenz R' in der Bildebene zu beziehen. Die Funktionen T(R') und Φ(R') kennzeichnen die Güte der optischen Übertragung (s.u.).

Nimmt die Phasenverschiebung Φ(R') speziell den Wert π an, so sind im Bild, verglichen mit dem Objekt, Hell und Dunkel vertauscht. Man spricht dann von Kontrastumkehr.

Im allgemeinen Falle ist die Änderung des Modulationsgrades bedingt durch eine Änderung sowohl der mittleren Intensität




(6)

als auch der Amplitude I₁ der Sinusschwingung


(7)

Aus den Faktoren d(0) und d(R') bestimmt sich die obige Größe T(R') nach (3) und (4) gemäß


(8)

Schließlich ist es zweckmäßig, die positive Größe d(R') mit der Phasenänderung Φ(R') zu einer komplexen Zahl


(9)

zusammenzufassen. Diese wird als o. Ü. bezeichnet. Die normierte o. Ü.


(10)

wurde früher als komplexe Kontrastübertragungsfunktion bezeichnet. Ihr früher Kontrastübertragungsfunktion genannter Betrag |D_N(R')|=T(R') heißt Modulationsübertragungsfunktion, die Phase Φ(R') von D(R') bzw. D_N(R') Phasenübertragungsfunktion.

Liegt eine allgemeine Intensitätsverteilung I(x,y) in der Objektebene vor, so kann man sich diese als eine Überlagerung von elementaren Sinusgittern vorstellen (Fourier-Transformation in der Optik). Es handelt sich dabei um zweidimensionale Gitter mit unterschiedlichen Gitterkonstanten in x- und y-Richtung, deren Kehrwerte die x- und die y-Komponente des Ortsfrequenzvektors angeben. Der Beitrag der einzelnen Sinusgitter zu I(x,y) wird dann durch das Ortsfrequenzspektrum b beschrieben, das sich, bezieht man zweckmäßigerweise die Intensitätsverteilung auf die Koordinaten x', y' in der Bildebene, zu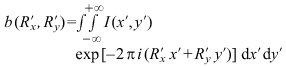


(11)

ergibt, wobei R'_x und R'_y die beiden Komponenten des Ortsfrequenzvektors R' in der Bildebene bezeichnen. Entsprechend lautet das Ortsfrequenzspektrum b'(R'_x, R'_y) für die Intensität I' (x', y') in der Bildebene


(12)

Da wegen der Linearität der optischen Übertragung (s.u.) die einzelnen Sinusgitter unabhängig voneinander transformiert werden, verknüpft die o. Ü. D(R'_x,R'_y) – in Verallgemeinerung der Gleichungen (5), (7) und (9) auf ein zweidimensionales Gitter – die Ortsfrequenzspektren (11) und (12) in der Form


(13)

Die Funktionswerte der o. Ü. sind die Übertragungsfaktoren für die einzelnen Ortsfrequenzen. Zur Erfassung der Kontrastumkehr ist es zweckmäßig, die normierte o. Ü. D_N in ihren Real- und Imaginärteil TcosΦ bzw. TsinΦ aufzuspalten und diese Funktionen als o. Ü. zu verwenden (Abb. 2).

Die formale Beschreibung vereinfacht sich, wenn man an Stelle der kartesischen Koordinaten x, y in der Objektebene bzw. x', y' in der Bildebene reduzierte Koordinaten X_O=(X_O, Y_O) bzw. X'=(X', Y') verwendet sowie reduzierte Ortsfrequenzvektoren W=(W_x, W_y) einführt (reduzierte Koordinaten), die sich bei der Übertragung nicht ändern. Die o. Ü. wird dann eine Funktion von W.

Voraussetzung für die Anwendung der o. Ü. ist neben dem Vorliegen von inkohärenter Abbildung die Invarianz des Punktbildes. Unter diesen Umständen erfolgt eine additive Überlagerung der von den verschiedenen Objektpunkten stammenden Intensitäten (und nicht der komplexen Amplituden), so daß die Übertragung (bezüglich der Intensität) linear ist.

Der Definitionsbereich für die o. Ü. ist durch die dem Auflösungsvermögen für Sinusgitter entsprechende reduzierte Grenzfrequenz |W|=2 begrenzt (Auflösungsvermögen 1)), bei der der Bildkontrast verschwindet. Entsprechend fällt die Modulationsübertragungsfunktion im Intervall 0≤|W|≤2 von 1 auf 0 ab (Abb. 2).

In Abbildungsketten (z.B. Kamera – Film – Vergrößerungsgerät – Photopapier) ergibt sich die gesamte o. Ü. als Produkt der o. Ü. der einzelnen, als linear im obigen Sinne vorausgesetzten Glieder. Es ist also über die Phasenübertragungsfunktionen zu summieren, während die Modulationsübertragungsfunktionen miteinander zu multiplizieren sind. Für ein aus mehreren Einzellinsen bestehendes Objektiv oder für aufeinanderfolgende Objektive ist dieses Vorgehen jedoch im allgemeinen nicht zulässig, weil vom jeweiligen Zwischenbild in der Regel mit Aberrationen und teilweise festen Phasenbeziehungen behaftete Wellen ausgehen und nicht unabhängig voneinander schwingende Kugelwellen.

Allgemein bestimmt sich die o. Ü. aus der Punktbildverwaschungsfunktion G'(X'-X_O). Da die Intensitätsverteilung I'(X') in der Bildebene durch Faltung der Intensitätsverteilung I_O(X_O) in der Objektebene mit G'(X'-X_O) hervorgeht (Verwaschungsfunktion, inkohärente Abbildung), ergibt sich die o. Ü. als die Fourier-Transformierte der Punktbildverwaschungsfunktion:


(14)

In der Praxis wird die o. Ü. im allgemeinen nur für eindimensionale Intensitätsverteilungen ermittelt. Die entsprechende eindimensionale o. Ü. ergibt sich dann als die Fourier-Transformierte


(15)

bzw.


(16)

der Linienbildverwaschungsfunktion L'(X'-X_L) bzw. des damit übereinstimmenden Kantengradienten

, wobei E'(X'-X_K) die Verwaschungsfunktion der Kante und X_L bzw. X_K die reduzierte Koordinate der Linie bzw. der Kante bezeichnen. Gleichungen (15) und (16) bilden die Grundlage der experimentellen Bestimmung der o. Ü. durch die Gitter-, Spalt- und Kantenbildanalyse (s.u.).

2) Die o. Ü. für optische Systeme.

a) Berechnung der o. Ü. Ausgehend von (14), ergibt sich die normierte o. Ü. unter Berücksichtigung des Zusammenhanges zwischen Punktbildverwaschungsfunktion, Amplitudenverwaschungsfunktion und Pupillenfunktion ψ'_B(X'_B), wobei X'_B=(X'_B, Y'_B) den Vektor der reduzierten Pupillenkoordinaten bezeichnet, von einem Normierungsfaktor A abgesehen, als das Autokorrelationsintegral der Pupillenfunktion, das Duffieux-Integral genannt wird,


(17)

Der Faktor A sorgt für die richtige Normierung D_N(0)=1. Für eine kreisförmige, unvignettierte, nicht apodisierte Pupille ist die normierte o. Ü. im Falle reiner Beugung bis auf einen Faktor gleich der Fläche des Überdeckungsgebietes der beiden um den Ortsfrequenzfaktor W gegeneinander verschobenen Pupillen


(18)

und fällt entsprechend von 1 bis zur Grenzfrequenz |W|=2 stetig auf 0 ab. Für sehr kleine (0≤|W|≤0,5) bzw. sehr große (1,5≤|W|≤2) Ortsfrequenzen kann man die beugungsbegrenzte o. Ü. durch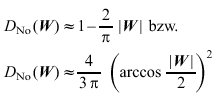


(19)

annähern. Infolge von Aberrationen und Defokussierung verschlechtern sich die Übertragungsfaktoren vor allem für mittlere Ortsfrequenzen (Abb. 2). In geometrisch-optischer Näherung kann das aberrationsbedingte Absinken der Modulationsübertragungsfunktion


(20)

für kleine Ortsfrequenzen durch das Gaußmoment 〈Δr'²〉 erfaßt werden. Das Produkt aus T_g(R') und der normierten beugungsbegrenzten o. Ü. D_No(R') entspricht für kleine Ortsfrequenzen näherungsweise der normierten o. Ü. D_N(R')=D_No(R')T_g(R').

Phasenverschiebungen, d.h. endliche Werte der Phasenübertragungsfunktion Θ(R') entstehen durch Verzeichnung und Koma und auch durch Defokussierung infolge von Bildfeldwölbung.

b) Polychromatische o. Ü. Bisher wurde Beleuchtung mit monochromatischem Licht vorausgesetzt. Häufig, z.B. in der Photographie, ist die Beleuchtung jedoch polychromatisch (vielfarbig). Die dann zu verwendende polychromatische o. Ü. ist gegeben als die mit der relativen spektralen Verteilung der Leuchtdichte B(λ) der Beleuchtung, der spektralen Transmission τ(λ) des optischen Systems und der relativen spektralen Empfindlichkeit F(λ) des Empfängers gewichtete Überlagerung der monochromatischen o. Ü. D(W,λ) im Spektralbereich (λ Wellenlänge)


(21)

Die polychromatische Modulationsübertragungsfunktion des dioptrischen Teils des menschlichen Auges kann ebenfalls nach (17) und (21) unter Berücksichtigung der gemessenen Aberrationen berechnet werden (Abb. 3).

c) Meßverfahren. Die experimentelle Bestimmung der o. Ü. erfolgt entweder durch Bildabtastverfahren mit nachfolgender Gitter-, Spalt- oder Kantenbildanalyse oder interferometrisch. Im ersten Falle wird ein Testobjekt (Gitter, Spalt, Kante oder Kreisblende mit einem Durchmesser von 1 bis 10 μm) durch das zu prüfende optische System abgebildet und die Bildintensitätsverteilung meist mit einem sehr schmalen Spalt (Breite b'=1/4πR

mit R

als Grenzfrequenz in der Bildebene) abgetastet, hinter dem ein Sekundärelektronenvervielfacher angeordnet ist. Die Abtastung kann auch objektseitig erfolgen. Als kombinierte Abtast- und Empfängereinheiten werden neuerdings CCD- oder Photodioden-Empfänger verwendet.

Für die Gitterbildanalyse werden als Testobjekte wegen der einfacheren Herstellung an Stelle von Sinusgittern meist Rechteckgitter benutzt, wobei in der Auswerteelektronik alle Oberwellen herausgefiltert werden.

Bei der Spalt- oder Kantenbildanalyse wird durch Abtasten des Bildes eines Spaltes bzw. einer Kante mit einem schmalen Abtastspalt die entsprechende Verwaschungsfunktion bestimmt, deren Fourier-Transformierte die o. Ü. des Gesamtsystems Objekt – optisches System – Abtastspalt ist. Diese Fourier-Transformation wird für die diskreten Meßwerte, deren Abstand nach dem Abtasttheorem der reziproken doppelten Grenzfrequenz entspricht, als einfache Summation durchgeführt. Wegen der oben genannten Multiplikativität der o. Ü. für lineare Abbildungsketten ergibt sich die o. Ü. des optischen Systems durch Division der gesamten o. Ü. durch die Fourier-Transformierte der Intensitätstransparenz des Objektes und des Abtastspaltes.

Bei der interferometrischen Messung der o. Ü. wird das Duffieux-Integral auf optischem Wege in einem Shearinginterferometer durch eine meßbare Pupillenverschiebung um W optisch nachgebildet. Die Intensität im Interferenzbild wird mit einem Phasenschieber, der die Phase einer Teilwelle verschiebt, kosinusförmig moduliert. Aus der Modulation dieser Kosinuskurve kann die o. Ü. berechnet werden.

d) Meßgeräte und experimentelle Resultate. Entscheidend für den verwendeten Meßgerätetyp sind die objekt- und bildseitigen Schnittweiten der Prüflinge. Um unendliche Schnittweiten zu simulieren, werden sehr gut korrigierte Kollimatoren benutzt, deren Aberrationen gegen die der Prüflinge vernachlässigbar sein sollen, was gewöhnlich durch eine mindestens fünfmal größere Brennweite des Kollimators erreicht wird. Die Meßgeräte besitzen große mechanische Stabilität, Präzisionsführungen für die Testobjekte und Abtastelemente, feinfühlige Fokussiermechanismen und genaue Drehvorrichtungen unter anderem für die Azimuteinstellung des Prüflings. Moderne Meßgeräte sind mit Mikrorechnern ausgerüstet.

Um einen Prüfling umfassend zu charakterisieren, sind oft über 100 Messungen der o. Ü. notwendig, z.B. in mehreren Bildhöhen, Azimuten, Einstellebenen, radialer und tangentialer Orientierung, mit verschiedenen Blenden, Abbildungsmaßstäben und sogar spektralen Strahldichteverteilungen der Beleuchtung. Die große Zahl der Meßkurven wird möglichst mit Bewertungsverfahren reduziert, um eine zusammenfassende Aussage über die Bildgüte zu erhalten. Abb. 4 zeigt die Modulationsübertragungsfunktion eines Photoobjektivs in Abhängigkeit von der Blendenzahl k. Sie wird optimal bei der "kritischen" Blendenzahl k=5,6 und verschlechtert sich bei größeren Blendenzahlen infolge der Beugung, bei kleineren Blendenzahlen infolge der sphärischen Aberration.

Abb. 5 läßt anhand der o. Ü. die hervorragende Korrektion eines photolithographischen Objektivs erkennen.

e) Pseudoübertragungsfunktion. Bei der partiell kohärenten Abbildung ist die Übertragung bezüglich der Intensität nicht mehr linear, so daß eine o. Ü. im strengen Sinne nicht existiert. Man kann in diesem Falle die Abbildungsleistungen optischer Systeme in Analogie zur o. Ü. durch die Menzelsche Pseudoübertragungsfunktion (Übertragungsfunktion der partiell kohärenten Abbildung) charakterisieren, die ebenfalls als Quotient der Fourier-Spektren der Bild- und der Objektintensitätsverteilung definiert ist. Da sie aber von der Objektstruktur und vom Kohärenzparameter abhängt (Abb. 5), besitzt sie nur eine eingeschränkte Aussagekraft.

3) Die o. Ü. von photographischen und streuenden Schichten. In diesem Falle ist die Phasenübertragungsfunktion ohne Bedeutung, und es interessiert ausschließlich die Modulationsübertragungsfunktion (MÜF) T(R'); sie ist die wichtigste Kenngröße zur Charakterisierung der Schärfe einer photographischen Abbildung. Typischerweise ist für sehr kleine Ortsfrequenzen R' der MÜF-Wert gleich Eins und geht mit wachsender Ortsfrequenz stetig gegen Null (Abb. 6). Dieser Abfall wird durch die Streuung, Absorption und Remission des Lichtes verursacht. Nachbareffekte, die durch die photographische Entwicklung bedingt sind (photographische Effekte), können bei kleinen Ortsfrequenzen zu Kontrastanhebungen T(R')>1 führen, wodurch sich unter anderem die Schärfe verbessert, die Übertragung jedoch nichtlinear wird.

Zur theoretischen Beschreibung der Modulationsübertragungsfunktion verwendet man die Friesersche Formel


, (22)

die nur die Effekte der Lichtstreuung und -absorption berücksichtigt. Dabei gibt ρ den Anteil des Lichtes an, der die Schicht ungestreut durchläuft, und die Friesersche Zahl k beschreibt die Ausbreitung des Streulichtes.

Bei Colormaterial sind die Verhältnisse aus verschiedenen Gründen komplizierter. Zum einen besteht der Farbfilm aus mehreren Schichten, von denen jede eine andere Modulationsübertragungsfunktion besitzt; zum anderen entsteht das Farbkorn nicht am Orte der Lichtabsorption, sondern dort, wo das abdiffundierende Entwickleroxidationsprodukt mit dem Farbkuppler reagiert. Diese Einflüsse verschlechtern im allgemeinen die Schärfe und damit die Modulationsübertragungsfunktion der Schichten zusätzlich.

Im Gegensatz zu den optischen Systemen ist im Falle der photographischen Schicht die "Bild"-Verteilung des Lichtes nicht direkt meßbar, weil sie sich im Inneren der Schicht ausbildet (innere Belichtungsverteilung). Die Grundidee der indirekten Messung besteht darin, die photographische Schicht selbst als ihr eigenes Photometer zu benutzen. Dazu wird die durch die innere Belichtung bewirkte Verteilung der Transparenz bzw. Schwärzung im photographischen Bild mit einem Mikrophotometer ausgemessen und von da unter Benutzung der charakteristischen Kurve auf die innere Belichtungsverteilung zurückgeschlossen. Diese Operation ist notwendig, weil kein linearer Zusammenhang zwischen der inneren Belichtung und der erzielten Schwärzung (bzw. Transparenz) besteht. Die weitere Verarbeitung der Meßwerte erfolgt je nach Verfahren wie in 2.3., wobei die äußere Belichtungsverteilung für die Objektseite und die innere Belichtungsverteilung für die Bildseite stehen. Zur Messung der Modulationsübertragungsfunktion werden den photographischen Schichten vorzugsweise periodische oder kantenförmige Beleuchtungsstärkeverteilungen (äußere Belichtungsverteilung) aufgeprägt.

Kennzeichnend für den Schärfeeindruck einer photographischen Abbildung ist die Modulationsübertragungsfunktion der gesamten Abbildungskette (z.B. Kamera – photographischer Film – Vergrößerungsgerät – Photopapier). Man gewinnt sie durch Multiplikation der einzelnen Modulationsübertragungsfunktionen.

Streuscheiben und Bildschirme verhalten sich bezüglich der Lichtstreuung wie photographische Schichten. Die Messung der Modulationsübertragungsfunktion ist einfacher, weil keine charakteristische Kurve existiert. Es braucht nur die von der Streuscheibe erzeugte Intensitätsverteilung mit einem Mikrophotometer gemessen und mit den Methoden der Bildabtastverfahren ausgewertet zu werden.

Optische Übertragungsfunktion 1: Übertragung einer sinusförmig modulierten Intensitätsverteilung aus dem Orts- in den Bildraum (Erläuterung s. Text).

Optische Übertragungsfunktion 2: Betrag (Modulationsübertragungsfunktion) T (a) und Realteil D_N (b) der normierten optischen Übertragungsfunktion D_N für den aberrationsfreien Fall (D_No) und für große Wellenaberrationen in Abhängigkeit von der x-Komponente

der reduzierten Ortsfrequenz W. λ₀ Vakuumwellenlänge,

des Ortsfrequenzvektors der Bildebene, n'sinσ' bildseitige numerische Apertur.

Optische Übertragungsfunktion 3: Modulationsübertragungsfunktion des menschlichen Auges in der Fovea für Tageslichtsehen (weißes Licht). R' Ortsfrequenz, d_Pup Pupillendurchmesser.

Optische Übertragungsfunktion 4: Modulationsübertragungsfunktion eines Photoobjektivs mit der Öffnungszahl 1,4/50 für weißes Licht. Bei jeder Blende wurde auf maximalen Wert der Modulationsübertragungsfunktion bei R' = 30 L/mm fokussiert. k Blendenzahl, R' Ortsfrequenz, y' Bildhöhe.

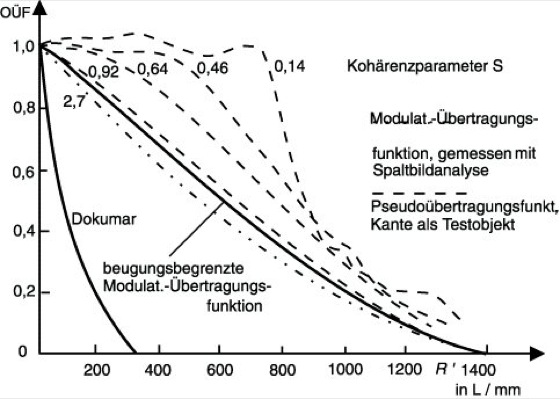
Optische Übertragungsfunktion 5: Gemessene optische Übertragungsfunktionen (OÜF) für ein photolithographisches Objektiv (Abbildungsmaßstab β' = -1:10, numerische Apertur sinσ' = 0,32, Wellenlänge λ = 436 nm, Bildhöhe y' = 0) im Vergleich mit einem Dokumar der Öffnungszahl 5,6/47 bei weißem Licht. R' Ortsfrequenz.

Optische Übertragungsfunktion 6: Modulationsübertragungsfunktion T(R') für Schwarzweiß-Negativfilme. R' Ortsfrequenz. (1) Mikroaufnahmefilm (Fuji HR II), (2) feinkörniger Aufnahmefilm (ORWO NP 15), (3) hochempfindlicher Aufnahmefilm (ORWO NP 27).