Lexikon der Physik: Fourier-Analyse
Fourier-Analyse
D. S. Broomhead, Manchester, England
Vermutlich werden alle Wissenschaftler und Ingenieure, zu diesem Thema befragt, der Ansicht zustimmen, daß die ›Fourier-Analyse‹ eine Angelegenheit von großer Bedeutung sei; jedoch fragt man dann, auf welche Weise sie bedeutend sei, so muß man sich auf eine Vielzahl verschiedener Antworten einstellen. Für den reinen Mathematiker war der Zeitpunkt, zu dem Fouriers Arbeiten entstanden, nämlich der Beginn des 19. Jh., ein Moment, in dem sich eine tiefgreifende Änderung im Verständnis der Grundlagen der Mathematik vollzog. Fouriers Herangehen an die Probleme der Wärmeleitung – Probleme, die wir aus heutiger Sicht eher dem Bereich der angewandten Mathematik oder den Ingenieurwissenschaften zuweisen würden – hat Fragen von fundamentaler Bedeutung für die gesamte Mathematik aufgeworfen; gleichzeitig lieferte Fouriers Ansatz ein bleibendes und mächtiges Werkzeug, das noch heute, zwei Jahrhunderte später, den Mathematikern und den Ingenieuren eine große Hilfe ist.
Wärmeleitung in einem dünnen Stab
Wir wollen mit einer Demonstration der Nützlichkeit dieses Werkzeugs beginnen. Die Wärmeleitung in einem Festkörper wird durch die Diffusionsgleichung
, (1)
beschrieben, in der κ die thermische Diffusivität des Festkörpers und θ eine Funktion ist, welche die Temperatur an einem beliebigen Punkt zu einer beliebigen Zeit t angibt. Der Einfachheit halber betrachten wir die Wärmeleitung in nur einer Raumdimension. Man nehme zum Beispiel einen zylindrischen Metallstab, der überall bis auf seine Endflächen isoliert ist, und der so dünn ist, daß kein merklicher Temperaturgradient quer zur Längsausdehnung auftreten kann. Wir wollen annehmen, daß sich der Stab von x = 0 zu x = π erstreckt; es mag unsinnig erscheinen, die Länge des Stabs als π zu wählen, aber es geht hier nur darum, eine passende Längeneinheit für unser Problem festzulegen.
Man sieht leicht (beispielsweise durch Einsetzen in die Gleichung), daß die folgenden Ausdrücke
Lösungen von Gleichung (1) sind, in denen μ eine freie Konstante ist. Aus der Linearität der Diffusionsgleichung folgt, daß wir weitere Lösungen durch Linearkombination obiger Lösungen gewinnen können. Diese einfache Beobachtung führt uns direkt zur Fourierschen Methode.
Wir wollen davon ausgehen, daß wir unseren Stab dazu gebracht haben, eine einheitliche Gleichgewichtstemperatur θ0 anzunehmen; dann, zur Zeit t = 0, tauchen wir ihn plötzlich in ein kaltes Bad ein, das in geeigneten Einheiten eine Temperatur von null aufweisen soll. Dies kann mathematisch durch
(4)
dargestellt werden. Dieser Ausdruck gibt zusammen mit den Randbedingungen
(5)
die anfängliche Temperaturverteilung wieder. Die Randbedingungen legen für alle Zeiten fest, daß die Temperatur an den Enden des Stabes gleich der Temperatur des Bades ist; dies entspricht der Annahme, daß das Bad gut durchmischt ist und eine sehr große Wärmekapazität aufweist.
Die Darstellung von Funktionen durch trigonometrische Reihen
Wir suchen nach einer Linearkombination von Lösungen der Form (2) und (3), welche die durch Gleichung (4) und (5) formulierten Randbedingungen erfüllt. Fouriers kühne Behauptung war nun, daß beliebige Anfangsbedingungen mit solchen Summen erfüllt werden können, wenn man μ über alle positiven ganzen Zahlen variieren läßt. Daher schreiben wir, indem wir die unbekannten Parameter 
und 
einführen:
(6)
und
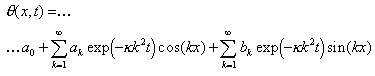
(7)
Der kritische Leser mag sich an diesem Punkt fragen, inwieweit es sinnvoll ist, mit unendlichen Summen von Funktionen zu hantieren, und mag der Behauptung, beliebige Funktionen könnten in dieser Weise dargestellt werden, skeptisch gegenüberstehen; wir werden uns diesen berechtigten Fragen später wieder zuwenden. Im Moment jedoch wollen wir untersuchen, inwieweit eine solche Darstellung bei der Lösung unseres Problems hilfreich sein könnte. Wenn wir die Bildung unendlicher Summen von Funktionen als möglichen Lösungsansatz akzeptieren, und wenn es uns gleichfalls sinnvoll erscheint, diese Summen gliedweise abzuleiten, so läßt sich durch Substitution von Gleichung (7) in Gleichung (1) zeigen, daß es sich tatsächlich um eine Lösung handelt. Darüber hinaus können wir die Einhaltung der Randbedingungen garantieren, indem wir alle Koeffizienten 
zu null setzen, so daß
(8)
und
(9)
Da sin(0) = 0 und sin(kπ) = 0 gilt, ist Gleichung (5) automatisch erfüllt.
Aber was ist mit der Anfangsbedingung an θ(x, 0)? Fouriers Idee war es, die unbekannten Koeffizienten 
so zu wählen, daß Gleichung (8) die Form von Gleichung (4) annimmt. Dies ist der Kerngedanke der Fourier-Analyse. Es geht an dieser Stelle ja nicht um die Lösung von Differentialgleichungen, sondern lediglich um die Darstellung einer Funktion als trigonometrische Reihe. In unserem Beispiel handelt es sich um eine Funktion, die auf dem offenen Intervall 0 x π einen von null verschiedenen konstanten Wert annimmt, jedoch an den Punkten x = 0 und x = π verschwindet. Der Gedanke, ein solches Objekt als eine einzelne Funktion zu behandeln oder gar als eine Summe von Sinuswellen darzustellen, erschien zu Fouriers Zeit als abwegig. Damals war die Erörterung der Frage, was die Eigenschaften einer Funktion ausmacht, untrennbar mit den Begriffen der Stetigkeit und der Differenzierbarkeit verknüpft, die jedoch ihrerseits noch nicht sauber definiert waren. Es dauerte noch über zwanzig Jahre, bis der strenge Beweis eines Theorems, das Fouriers Behauptung enthielt, veröffentlicht wurde.
Der Dirichletsche Satz
Dieses von Dirichlet gefundene Theorem ist, obgleich seither allgemeinere Ergebnisse bewiesen werden konnten, für viele Anwendungen ein nützliches Werkzeug. Dirichlet zeigte, daß unter der Voraussetzung, daß eine auf dem Intervall [-π, π] definierte Funktion F stückweise stetig und stückweise monoton ist, eine eindeutig festgelegte Fourier-Reihe existiert, die an jedem Punkt x, an dem F stetig ist, gegen F(x) konvergiert. An jeder Unstetigkeitsstelle konvergiert die Fourier-Reihe gegen den Mittelwert des rechtsseitigen und des linksseitigen Grenzwertes von F an dieser Stelle.
Wie man eine Fourier-Reihe konstruiert
Der direkteste und eleganteste Weg, die passenden Fourier-Koeffizienten zu einer gegebenen Funktion F zu finden, besteht darin, die Orthogonalitätsrelationen der trigonometrischen Funktionen auszunutzen, die für Sinus-Funktionen von der folgenden Form sind:
(10)
Analoge Relationen gelten für die Kosinus-Funktion. Darüber hinaus läßt sich auch
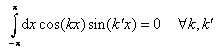
(11)
zeigen. Zu Demonstrationszwecken wollen wir in einem kleinen Exkurs folgende auf dem Intervall -π x π definierte Funktion betrachten:
Diese Funktion, die aus einsichtigen Gründen als Stufenfunktion bezeichnet wird, ist offenbar stückweise stetig und monoton. Sie weist genau eine Unstetigkeitsstelle, nämlich bei x = 0, auf, und sie ist so definiert, daß ihr Wert an dieser Stelle gleich dem Mittelwert aus rechts- und linksseitigem Grenzwert ist. Daher können wir die Stufenfunktion unter Ausnutzung des Dirichletschen Satzes als Fourier-Reihe schreiben:
(12)
Wenn wir beide Seiten dieser Gleichung mit 
multiplizieren und anschließend über x von -π bis π integrieren, wobei aus der Orthogonalitätsrelation folgt, daß sämtliche der unendlich vielen Integrale auf der rechten Seite bis auf eines verschwinden, so ergibt sich:
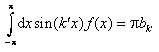
(13)
In analoger Weise, nämlich durch Multiplikation mit 
und anschließender Integration, bekommt man einen Ausdruck für 
:
(14)
Das Schöne an diesem Verfahren ist, daß es explizite Ausdrücke für die Entwicklungskoeffizienten in Form von Integralen über die bekannte Funktion f liefert.
Für die Stufenfunktion sind diese Integrale besonders leicht auszuführen, da es sich bei ihr um eine ungerade Funktion handelt, die dementsprechend die Symmetriebeziehung f(x) = -f(-x) erfüllt. Damit erhält man:
, (15)
woraus folgt, daß alle Koeffizienten 
verschwinden, so daß die in Gleichung (12) dargestellte Reihe nur aus Sinus-Termen besteht. Auf ähnliche Weise findet man
(16)
Unsere Fourier-Reihe für f(x) reduziert sich also auf eine Summe von Sinus-Funktionen, deren Argumente ungeradzahlige Vielfache von x sind:
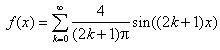
(17)
In der Praxis wäre es oftmals wünschenswert, diese unendliche Summe durch ihre ersten (möglichst wenigen) Glieder annähern zu können. Wie sinnvoll dies ist, hängt davon ab, wie schnell die Reihe konvergiert – daß die Reihe überhaupt konvergiert, und zwar gegen die richtige Funktion, wissen wir bereits aus dem Dirichletschen Satz. Aus Abb. 1 , in der verschiedene Näherungen von Gleichung (17) dargestellt sind, können wir entnehmen, daß die Reihe doch eher langsam konvergiert – selbst wenn man die Glieder bis zu k = 30 berücksichtigt, zeigt die Näherung besonders in der Nähe der Singularität bei x = 0, aber auch noch in der Nähe von x = -π und x = π, starke Oszillationen.
Da trigonometrische Funktionen auf dem gesamten Bereich der reellen Zahlen wohldefiniert sind, kann jede beliebige Fourier-Reihe wie eine Funktion von ganz 
behandelt werden; dies sogar dann, wenn man sie damit über den Definitionsbereich der Funktion, die dargestellt werden soll, hinaus erweitert. Dieser Aspekt impliziert, daß jede Fourier-Reihe (und damit auch die zugrundeliegende Funktion f) periodisch sein muß; in unserem Beispiel ergibt sich f(x + 2π) = f(x) aus der Periodizität der Sinus-Funktionen in den Gliedern der Reihe. In diesem Sinne stellt sich die Fourier-Reihe, obwohl sie auf dem beschränkten Definitionsbereich der Originalfunktion f wie eine Stufenfunktion aussieht, auf dem erweiterten Definitionsbereich als eine periodische, stückweise konstante Funktion dar. Letztere weist zusätzlich zu der Unstetigkeitsstelle bei x = 0 eine solche bei x = π und, dies erfordert die Periodizität, auch bei x = -π auf. Man kann aus dem Dirichletschen Satz oder auch schlicht aus der Tatsache, daß sin((2k + 1)π) = 0 gilt, folgern, daß f(π) = 0 gilt.
Die Lösung der Wärmeleitungsgleichung
Daß wir diese Überlegungen bei der Lösung des Wärmeleitungsproblems gebrauchen können, erkennt man, wenn man die Funktion f durch ihre Fourier-Reihe darstellt, deren Definitionsbereich man auf das Intervall 0 ≤ x ≤ π einschränkt. Dann nämlich kann man die Anfangsverteilung der Temperatur als
(18)
schreiben. Daraus ergibt sich, daß die gesamte Zeitentwicklung der Temperaturverteilung des Stabes durch
(19)
gegeben ist. Diese Lösung ist in Abb. 2 dargestellt; offenbar verliert die Verteilung ihre anfängliche charakteristische rechteckige Form sehr schnell. Dies hat mit der langsamen Konvergenz der Fourier-Reihe für f(x) zu tun: Jede Näherung der vollen Fourier-Reihe durch endlich viele Glieder ist ein Versuch der Darstellung einer unstetigen Funktion mit einer glatten, denn der Gradient einer solchen Näherung kann eine Grenze gemäß
(20)
nicht überschreiten. Intuitiv erwarten wir, daß die Unstetigkeiten von f(x) durch solche Stellen der endlichen Reihe angenähert werden, die einen sehr steilen Verlauf aufweisen; um dies zu erreichen, brauchen wir große K, also schnell oszillierende Sinus-Funktionen. Für die Lösung der Diffusionsgleichung (19) gilt, daß die Sinus-Funktion um so schneller bei der zeitlichen Entwicklung abfällt, je höher ihre Frequenz ist; daher glättet sich die eckige Form der Anfangsverteilung schnell.
Weitere Entwicklungen und Anwendungen
Wir haben bereits weiter oben darauf hingewiesen, daß es heikel ist, unendliche Summen wie endliche zu behandeln. Um die Fourier-Analyse zur Lösung von Differentialgleichungen verwenden zu können, müssen wir wissen, ob es erlaubt ist, die Reihe gliedweise abzuleiten. Das ist offenbar nicht selbstverständlich; die Fourier-Reihe der Stufenfunktion beispielsweise ist nicht einmal stetig, geschweige denn stellt sie eine Summe differenzierbarer Funktionen dar. Damit eine Fourier-Reihe stetig ist, reicht es jedoch schon hin, wenn sie gleichmäßig konvergent ist – dies ist im wesentlichen eine Bedingung, die sicherstellt, daß die Reihe über den ganzen Definitionsbereich schnell genug konvergiert. Damit eine Fourier-Reihe differenzierbar ist, genügt es, daß die Reihe, die durch gliedweise Ableitung der Originalreihe entsteht, gleichmäßig konvergiert. Zu der Zeit, zu der diese Gedanken ausgearbeitet wurden, herrschte eine beträchtliche Verwirrung bezüglich des Zusammenhangs zwischen Stetigkeit und Differenzierbarkeit. Man hatte irgendwie das Gefühl, daß eine stetige Funktion nur an wenigen besonderen Stellen nicht differenziert werden kann. Diese Illusion zerschlug sich, als Weierstraß 1872 auf folgende Funktion hinwies, die explizit als trigonometrische Reihe definiert ist:
(21)
Ist a eine ungerade ganze Zahl, und gilt 0 b 1 und ab > 1 + 3π/2, so ist diese Funktion für alle x stetig, jedoch nirgendwo differenzierbar. Aus der Sicht heutiger Entwicklungen der Geometrie fraktaler Mengen und ihrer Anwendung auf die Beschreibung von Naturphänomenen müssen wir den Graphen dieser Funktion als ein frühes Beispiel eines mathematisch konstruierten Fraktals betrachten.
Die Fourier-Analyse hat aufgrund der Nützlichkeit des Verfahrens beim Lösen linearer Differentialgleichungen einen weiten Anwendungsbereich. Die Diffusionsgleichung (1) und ihr verwandte Gleichungen tauchen in so verschiedenartigen Gebieten wie der elektrischen Leitfähigkeit, der selbständigen Durchmischung von in Flüssigkeiten und Gasen gelösten Materialien, der Wahrscheinlichkeitstheorie und neuerdings sogar bei der Berechnung der zukünftigen Entwicklungen von Finanzmärkten auf. Der Diffusionsgleichung sehr nah verwandt ist die Schrödinger-Gleichung, die von zentraler Bedeutung für die Quantenmechanik ist. Fourier-Reihen können eingesetzt werden, um die Wellengleichung zu lösen, die von der mathematischen Nachbildung schwingender Saiten und Orgelpfeifen bis hin zur Beschreibung der Ausbreitung elektromagnetischer Wellen nahezu überall Anwendung findet. Selbst bei der Behandlung nichtlinearer Gleichungen kann die Fourier-Analyse von großem Nutzen sein, weil es oftmals möglich ist, die Stabilität einer Lösung der vollen nichtlinearen Gleichung zu überprüfen, indem man lineare Gleichungen ableitet, welche die Entwicklung kleiner Störungen des gegeben Zustands beschreiben. In solchen Analysen kann man auf Lösungen, die der Form von Gleichung (7) ähneln, stoßen, wobei jedoch einige der Koeffizienten exponentiell ansteigen. Solche Lösungen bilden eine neue Generation räumlicher Strukturen auf dem Gebiet nichtlinearer Gleichungen.
Schließlich wollen wir darauf hinweisen, daß es noch weit mehr mathematische Techniken gibt, die sich mit Fouriers Namen verbinden, als hier im zur Verfügung stehenden Raum auch nur erwähnt werden kann. Von diesen vielleicht am weitesten verbreitet ist das Fourier-Integral, das als Erweiterung der Fourier-Reihe verstanden werden kann. Wenn wir den ganzzahligen Index k in Gleichung (12) als reelle Variable uminterpretieren und die Summenzeichen durch Integrale ersetzen, so gelangen wir zu einem Konstruktionsverfahren für Funktionen f(x), die nicht mehr zwingend periodisch sein müssen. Bei dieser Verallgemeinerung sind die Fourier-Koeffizienten 
und 
Funktionen der reellen Variablen k, die als Fourier-Transformierte von f(x) bezeichnet werden. Diese Verallgemeinerung ist bei der Behandlung von Differentialgleichungen über einem unendlichen Definitionsbereich, bei der Zeitreihenanalyse und in der Spektroskopie von größter Bedeutung.
Ganz zum Schluß sollten wir uns vielleicht zurücklehnen und einen Moment darüber nachsinnen, daß die Geschichte der Fourier-Reihen ein sehr schönes Beispiel für das ist, was die Mathematik und die Wissenschaften allgemein in den letzten drei Jahrhunderten hat so erfolgreich sein lassen. Es ist eine Geschichte darüber, wie Anwendungen die Entwicklung der reinen Mathematik vorantreiben und dann wiederum die Entwicklungen in der reinen Mathematik zu neuartigen, oftmals unerwarteten Anwendungen führen.
![](javascript:ShowPic("/lexika/images/physik/fff3964.jpg", "319", "198");)
Fourier-Analyse 1: Darstellung vier verschiedener Näherungen von Gleichung (17), an denen man die Auswirkung der Hinzunahme weiterer Glieder beobachten kann. Man beachte, daß der Graph um so mehr Oszillationen aufweist, je mehr Glieder berücksichtigt werden.
![](javascript:ShowPic("/lexika/images/physik/fff3967.jpg", "331", "252");)
Fourier-Analyse 2: Eine Darstellung von θ(x, t) für den abkühlenden Stab.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.