Methode der kleinsten Quadrate

Josef Kallrath, Ludwigshafen

Im Jahre 1805 publizierte A. Legendre als erster einen Aufsatz über die Methode der kleinsten Quadrate (MdkQ) und wandte sie auf die Auswertung der im Jahre 1795 gewonnenen Daten der Vermessung des französischen Meridians an. Im Jahr 1809 erbringt F. Gauß, der behauptet, die MdkQ schon seit 1795 zu benutzen, in Theoria Motus Corporum Coelestium die Begründung der Methode auf Basis normalverteilter Fehler. Er zeigt ferner, wie sich die Fehler der bestimmten Parameter schätzen lassen und sich die Methode auf nichtlineare Probleme durch Linearisierung erweitern läßt. Tatsächlich scheint Gauß die MdkQ seit 1795 benutzt zu haben, ist aber durch Legendres Veröffentlichung vermutlich erst auf die weitreichende Bedeutung dieser Methode aufmerksam geworden.

Seit den Tagen von Legendre und Gauß hat die Methode viele Verbesserungen und Erweiterungen erfahren. Stabile numerische Verfahren wurden entwickelt, um große Datenmengen auszuwerten, um Ausgleichsprobleme mit stochastischen Randbedingungen zu lösen, um die unabhängige Meßgröße (meist Zeit) ebenfalls als fehlerbehaftet zu behandeln (total least squares) oder um die Methode auf Modelle anzuwenden, denen Differentialgleichungsmodelle zugrunde liegen. Die Lösung von Ausgleichsproblemen in Verbindung mit Differentialgleichungsmodellen ist sehr wesentlich für die physikalisch-fundierten Naturwissenschaften, aber auch z.B. für die Biologie. Ein schwerwiegender Nachteil der klassischen MdkQ ist die Beschränkung, daß explizite Modelle – meist Geraden oder Polynome – angepaßt werden. Da viele naturwissenschaftliche Fragestellungen, z.B. bei der Untersuchung dynamischer Systeme in Physik, Astronomie und Astrophysik, aber auch in der Ökologie, jedoch auf Differentialgleichungen führen, deren Lösungen nicht in geschlossener Form dargestellt werden können, gewinnen numerische Verfahren an Bedeutung, die die MdkQ mit Differentialgleichungsansätzen verbinden und die Differentialgleichungen als diskretisierte Nebenbedingungen simultan mit einbeziehen; dieser Ansatz läßt sich übrigens auf jegliche Art implizit vorgegebener Modelle erweitern und führt in natürlicher Weise auf Verfahren zur optimalen Steuerung.

1 Unbeschränkte Ausgleichsprobleme

Ein unbeschränktes Ausgleichsproblem mit n freien Parametern

im Sinne der Methode der kleinsten Quadrate kann als ein unbeschränktes Minimierungsproblem mit einer Zielfunktion der Form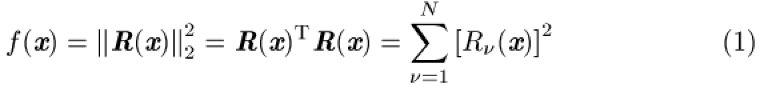

mit

aufgefaßt werden. Diese Form resultiert z.B. aus einem nichtlinearen überbestimmten Gleichungssystem

oder einem Ausgleichsproblem mit N gegebenen Datenpunkten

und Varianzen

, einer Modellfunktion

und n zu bestimmenden Parametern

:

Die Gewichte

leiten sich aus den Varianzen

gemäß der Beziehung

ab, mit einem passend gewählten Skalierungsfaktor, der die Gewichte möglichst in der Größenordnung 1 hält. In der kürzeren Vektorschreibweise erhält man für den Residuenvektor

mit

. Der Residuenvektor (2) beschreibt den auf die unabhängige Koordinatenachse (t mit Index ν) projizierten Abstand. In manchen Anwendungen wird stattdessen auch der orthogonale Abstand eines Meßpunktes von der Modellkurve als Maß der Güte verwendet (total least squares, TLS). Im Falle von TLS hat der Residuenvektor

die Gestalt

Zu beachten ist, daß die vormals unabhängige Größe

jetzt ebenfalls mit Hilfe der MdkQ bestimmt wird. TLS-Probleme sind immer nichtlinear.

Es ist wichtig, bei praktischen Anwendungen ein verläßliches Maß für die Varianzen und damit für die Gewichte im Ausgleichsfunktional zu haben und auch sicherzustellen, daß die Fehler der Messungen normalverteilt sind.

Vor Behandlung des allgemeinen nichtlinearen Falles ist es sinnvoll, zunächst den linearen Fall

zu behandeln, da das lineare Ausgleichsproblem in der iterativen Lösung des nichtlinearen Falls als häufig zu lösendes Unterproblem auftritt.

Der lineare Fall: Die Normalgleichungen

Der gewichtete Residuenvektor

mit

und

ist linear in

und führt zu einem linearen Ausgleichsproblem im Sinne der kleinsten Quadrate

mit konstanter Matrix

. Ein Spezialfall des linearen Ausgleichsproblems ist die lineare Regression, der das Problem zugrunde liegt, durch eine Menge von Meßpunkten eine Gerade zu legen. Das lineare Ausgleichsproblem besitzt mindestens eine Lösung

, die jedoch nicht notwendigerweise eindeutig ist. Bezeichnet

eine weitere Lösung, so gilt

. Alle Lösungen von (3) erfüllen die Normalgleichungen

als notwendige Bedingungen. Lösungen von (4) sind ihrerseits Lösungen von (3), d.h. die Normalgleichungen sind die notwendigen und hinreichenden Bedingungen für die Existenz und Bestimmung der Ausgleichslösung im Sinne der kleinsten Quadrate.

Der Betrag

des Residuenvektors

der Lösung ist eindeutig bestimmt durch

Hat

vollen Rang, so besitzt (3) eine eindeutige Lösung und es existiert eine eindeutige Lösung für

, die als Lösung des linearen Gleichungssystems

bestimmt werden kann. In diesem Fall gilt

, d.h. die symmetrische Matrix

hat vollen Rang. Unter numerischen Gesichtspunkten sollten Ausgleichsprobleme möglichst nicht direkt mit Hilfe der Normalgleichungen gelöst werden, da hier aus den folgenden Gründen große Vorsicht geboten ist:

• die Berechnung

erfordert die Auswertung von Skalarprodukten (wegen des Verlustes signifikanter Stellen bei Addition und Subtraktion von Zahlen ähnlicher Größenordnung sollte dies vermieden werden);

• mögliche große Fehlerfortpflanzung der Fehler des Terms

der rechten Seite bei der Lösung der Normalgleichungen, da die Fehlerfortpflanzung proportional zur Konditionszahl

ist; mißt man die Norm einer Matrix in der euklidischen Norm, so ist

gerade das Verhältnis des größten zum kleinsten Eigenwert.

Mit Hilfe von Orthogonalisierungsverfahren kann das lineare Ausgleichsverfahren nur mit Hilfe der Matrix

gelöst werden und bedarf nicht des Produktes

.

Der lineare Fall: Ein Orthogonalisierungsverfahren

Numerische Probleme, die sich aus großen Konditionszahlen von

ergeben, können begrenzt werden, indem man sich auf Lösungsverfahren beschränkt, die nur auf

direkt aufbauen. Orthogonalisierungsverfahren zur Lösung linearer Ausgleichsprobleme basieren auf orthogonalen Transformationen

; diese lassen die euklidische Norm von Matrizen invariant und führen zu numerisch stabilen Verfahren zur Lösung von Ausgleichsproblemen. Householder-Transformationen sind eine spezielle Variante othogonaler Transformationen. Die Matrix

wird dabei so transformiert, daß

1) die Lösung des Problems unverändert bleibt,

2) die Konditionszahl

der transformierten Matrix nicht größer als

ist und

3) die transformierte Matrix

eine triangulare Struktur hat, die sich gut für numerische Berechnungen eignet.

Sei

, eine Folge von Householder-Transformationen, d.h. von speziellen Matrizen der Form

wobei

die

-Einheitsmatrix und

einen beliebigen n-dimensionalen Vektor bezeichnet. Householder-Transformationen

sind Spiegelungen des Vektorraums

bezüglich des orthogonalen Komplements

und sind unitär, ebenso wie das Produkt

. Der Vektor w kann nun derart gewählt werden, daß

einen gegebenen Vektor

, dessen erste Komponente von Null verschieden ist (falls

, kann dies durch geeignete Permutation stets erreicht werden; im Fall

ist nichts zu tun), auf ein Vielfaches des ersten Einheitsvektors

abbildet, d.h.

Für einen von Null verschiedenen Vektor impliziert dies die folgenden Formeln zur Berechnung von Householder Transformationen:

Hat die Matrix

n linear unabhängige Spaltenvektoren

, so lassen sich die Matrizen

und der Vektor

des linearen Ausgleichsproblems (3) letztlich mit Hilfe von

in eine Matrix

mit einer einfacheren Struktur,

und einen Vektor

transformieren; ferner ist

eine obere Dreiecksmatrix. Wie in der Numerik üblich, wird aus Gründen der Genauigkeit und Stabilität

nicht direkt als Matrizenprodukt ausgewertet, sondern sukzessive als Folge von Householder-Transformationen und Modifikationen von

erstellt.

Damit nimmt das ursprüngliche Problem (3) die Gestalt

an. Wegen der Verwendung der euklidischen Norm und der Unitarität von

erhält man

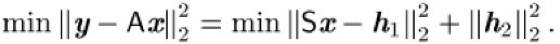
Da

ein konstanter Vektor ist, nimmt

sein Minimum an, wenn der unbekannte Vektor x Lösung des linearen Gleichungssystems

ist. Daher löst

schließlich das lineare Ausgleichsproblem in euklidischer Norm. Die obere Dreiecksmatrix

besitzt genau dann und nur dann eine eindeutige inverse Matrix, wenn

. Da

regulär ist, ist die Regularität von

äquivalent zur Regularität von

.

Der nichtlineare Fall: Ein Gauß-Newton Verfahren

Um das nichtlineare Problem (1) zu lösen, kann man es als unbeschränktes Optimierungsproblem behandeln, indem man auf dem Gradienten

und der Hesse-Matrix

aufbaut. Über diesen Zugang leitet man die notwendigen Bedingungen ab, linearisiert sie und erzeugt letztlich wieder die Normalgleichungen; aus numerischen Gründen wie oben diskutiert wird dieser Weg nicht empfohlen. Trotzdem ist es gut, seine Strukur zu kennen.

In einem Ausgleichsproblem mit euklidischer Norm hat der Gradient

von

die einfache Gestalt

wobei

die Jacobi-Matrix von

bezeichnet. Die Hessematrix

von

ist

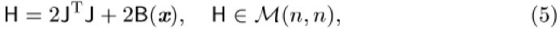
mit

Sind die zweiten Ableitungen

verfügbar, dann kann (5) in der quasi-Newton Methode verwendet werden. In den meisten Fällen ist es aber möglich, stattdessen eine typische Eigenschaft von Ausgleichsproblemen auszunutzen. Die Residuen

werden im Lösungspunkt

gewöhnlich recht klein sein und

kann unter dieser Annahme kleiner Residuen mit

approximiert werden. Diese Approximation der Hesse-Matrix erhält man auch, wenn man die Residuen

entwickelt und bis zur linearen Ordnung mitführt. Der Vorteil, und dies resultiert aus der speziellen Struktur der MdkQ, liegt darin, daß Informationen über die zweite Ableitung komplett aus Ableitungen erster Ordnung gewonnen werden. Dies ist typisch für Ausgleichsprobleme, und diese spezielle Variante des Newton-Verfahrens wird Gauß-Newton-Methode genannt. Gedämpfte Gauß-Newton-Verfahren bedienen sich eines Liniensuchverfahrens, um aus einer vorliegenden Lösung

in der k-ten Iteration

zu erhalten, und gehen wie folgt vor:

• Bestimmung der Suchrichtung

aus dem linearen Gleichungssystem

das sich aus dem klassischen Newton-Verfahren bei Optimierungsfragestellungen, d.h. den Bedingungen

, ableitet;

• Anwendung des Liniensuchverfahrens zur Bestimmung des Dämpfungsfaktors

• Iteration

.

Das Gauß-Newton-Verfahren und seine Konvergenzeigenschaften hängen stark von der Approximationgüte der Hesse-Matrix ab. In Problemen mit relativ großen Residuen wird

in Formel (5) an Bedeutung zunehmen und die Konvergenzrate abnehmen. Für

und hinreichend nahe der optimalen Lösung konvergiert das Gauß-Newton-Verfahren nur mit linearer Konvergenzrate. Nur für

kann eine quadratische Konvergenz erzielt werden. Trotz dieser Nachteile stellt es ein klassisches, wenn auch hier nicht empfohlenes Verfahren zur Lösung nichtlinearer Ausgleichsprobleme dar.

Zu beachten ist, daß die linearen Gleichungen (6), die in jeder Iteration k gelöst werden müssen, die Normalgleichungen des Ausgleichsproblems

mit

,

,

sind.

Eine beliebte Methode zur Lösung unbeschränkter nichtlinearer Ausgleichsprobleme ist der Levenberg-Marquardt-Algorithmus, der 1944 von Levenberg und unabhängig davon 1963 von Marquardt vorgeschlagen wurde. Dieses Verfahren modifiziert die Eigenwerte der Matrix

und versucht den Einfluß der Eigenvektoren, die zum kleinsten Eigenwert gehören, zu reduzieren.

Im Zusammenhang mit linearen Ausgleichsproblemen zeigten Orthogonalisierungsverfahren einen Weg auf, die numerischen Probleme zu umgehen, die sich bei der Lösung der Normalgleichungen ergeben. Führt man die Linearisierung des nichtlinearen Ausgleichsproblems ein wenig verschieden durch, so gewinnt man ein Gauß-Newton-Verfahren, das die Bildung der Normalgleichungen umgeht. Hierzu wird die Taylor-Reihenentwicklung des Residuenvektors

in erster Ordnung betrachtet:

Die notwendigen Bedingungen zur Lösung von (8) sind wieder die Normalgleichungen von (7). Dies zeigt, daß die Lösungen von (8) und des ursprünglichen Problems identisch sind. Die in (8) verwendete Entwicklung ist allerdings nur dann eine gute Approximation des ursprünglichen Problems, wenn gilt:

• der Residuenvektor

, oder äquivalent dazu

, ist hinreichend klein; oder

• die Differenz

ist hinreichend klein.

In gedämpften Gauß-Newton-Verfahren mit Dämpfungsparameter

ist das ursprüngliche Problem (8) daher ersetzt durch

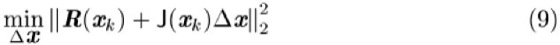
mit einem nachgeschalteten Liniensuchverfahren. Zunächst wird also das lineare Ausgleichsproblem (9) mit

und

z.B. mit dem Householder-Verfahren gelöst; das Ergebnis ist die Suchrichtung

. In der Iteration wird dann

gesetzt, wobei der Dämpfungsfaktor

mit Hilfe eines Liniensuchverfahren oder natürlicher Niveaufunktionen gewonnen wird.

2 Beschränkte Ausgleichsprobleme

Beschränkte Ausgleichsprobleme der Form

werden oft mit dem in der beschränkten Optimierung bekannten Verfahren der sequentiellen quadratischen Programmierung gelöst; dieser Zugang ist aber nur bedingt zu empfehlen. Sinnvoller ist es, verallgemeinerte Gauß-Newton-Verfahren in Verbindung mit Orthogonalisierungstechniken zu verwenden.

Gauß-Newton-Verfahren für beschränkte Ausgleichsprobleme

Formal soll ein Ausgleichsproblem mit

Randbedingungen der Form

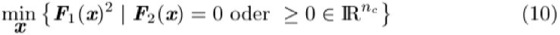
mit Residuenvektor

gelöst werden. Hier sei nur der gleichungsbeschränkte Fall betrachtet. Als Startwert sei

gegeben; die Iteration verfährt in der Form

mit einer Dämpfungskonstante

, die nicht beliebig klein werden soll, d.h.

. Zur Berechnung des Inkrementes

wird

in (10) durch

substituiert und die Terme

und

um

linearisiert. Dann ist

Lösung des linearen, gleichungsbeschränkten Ausgleichsproblems

mit den Jacobi-Matrizen

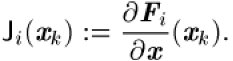
Unter bestimmten Annahmen über die Regularität der Jacobi-Matrizen

existiert eine eindeutige Lösung

von (11) und eine eindeutige lineare Abbildung

(die verallgemeinerte Inverse genannt wird und nicht mit der Moore-Penrose-Inversen (Matrix) verwechselt werden darf), die den Bedingungen

genügt. Die Lösung

des linearen Problems folgt eindeutig aus den Kuhn-Tucker-Bedingungen (Lagrange-Multiplikatoren)

wobei

den Vektor der Lagrange-Multiplikatoren bezeichnet.

Zur numerischen Berechnung von

wird die verallgemeinerte Inverse nicht explizit berechnet. Stattdessen werden Verfahren entwickelt, die die Struktureigenschaften der Jacobi-Matrizen ausnutzen und spezielle Faktorisierungen von

und

verwenden. Da die Jacobi-Matrizen und ihre Zerlegungen in jeder Iteration bekannt sind, lassen sich nach Konvergenz Kovarianz- und Korrelationsmatrix für den Lösungsvektor

ausrechnen.

Parameterbestimmung in Systemen von Differentialgleichungen

Mit Hilfe eines Mehrzielansatzes können auch Differentialgleichungssysteme mit geringen Stabilitätseigenschaften und selbst chaotische Systeme untersucht werden. Gegeben seien eine Differentialgleichung (mit Schaltbedingungen) für die Zustandsvariable

mit einer von einem Parametervektor

abhängigen rechten Seite, Anfangsbedingungen

sowie Meßwerten

für die Zustandsvariablen

oder allgemeiner für Funktionen derselben,

die zu Zeiten

(den Meßpunkten) in einem Zeitraum

erhoben wurden und mit einem Meßfehler

behaftet sind. Sind die Meßfehler

unabhängig sowie normalverteilt mit Mittelwert Null und sind ihre Varianzen

bekannt, so ist ein angemessenes Zielfunktional durch

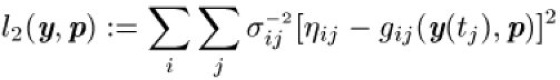
gegeben. Insbesondere der Parametervektor

, aber auch die Trajektorien

können Gleichungs- und Ungleichungsbedingungen unterworfen werden, so daß zusätzlich bekannte Informationen über die zu identifizierenden Parameter, z.B. Positivitätsforderungen, in der Problemformulierung berücksichtigt werden können.

Ein naheliegender und häufig verwendeter Ansatz zur numerischen Behandlung von Parameteridentifizierungsproblemen bei Differentialgleichungen besteht in der wiederholten Lösung des Anfangswertproblems (AWP) für feste Parameter innerhalb einer iterativen Prozedur zur Anpassung der Parameter, um die Approximation zu verbessern. Das inverse Problem wird also wieder auf eine Folge von AWP zurückgeführt. Diese Reinversion des inversen Problems eliminiert die Zustandsvariablen

zugunsten der unbekannten Parameter

. Dies hat zur Folge, daß jegliche Information über den Lösungsverlauf, die für das inverse Problem gerade charakteristisch ist, außer Acht gelassen wird; dies wiederum hat einen verkleinerten Konvergenzbereich zur Folge. Durch schlechte Startwerte der Parameter kann man zudem in schlecht konditionierte Bereiche des AWPs kommen, was zum Verlust der Stabilität führen kann, oder die Lösung läuft in eine Polstelle, so daß gar nicht für alle Meßwerte das Ausgleichsfunktional ausgewertet werden kann.

Alternativ zum AWP-Ansatz kann das inverse Problem als überbestimmtes, beschränktes Mehrpunktrandwertproblem mit Schalt- und Sprungbedingungen aufgefaßt werden, und zwar unabhängig davon, ob das ›direkte‹ Problem auf Grund der Modellbedingungen ein Randwertproblem darstellt oder nicht. Dies ermöglicht insbesondere auch die Modellierung dynamischer Prozesse, die nicht durch Differentialgleichungen mit glatter rechter Seite beschrieben werden. Sie werden dann als Differentialgleichungen mit Schaltbedingungen formuliert,

wobei sich die rechte Seite bei einem Vorzeichenwechsel der Schaltfunktion

unstetig ändert. Solche Unstetigkeiten können z.B. durch sprunghafte Änderungen physikalischer Größen oder Gesetzmäßigkeiten auftreten. Die Schaltpunkte sind dann implizit durch

gegeben. Schaltpunkte können auch explizit gegeben sein; ebenso ist es möglich, daß Unstetigkeiten der Zustandsvariablen selbst vorkommen.

Für ein gewähltes und an das Problem wie auch an die Meßwerte angepaßtes Gitter

von m Stützstellen

(

Teilintervalle

),

welches das Meßintervall überdeckt (

), wird die diskrete Trajektorie

als Variable neben den unbekannten Parametern

eingeführt; die

sind dabei die Anfangswerte der Teiltrajektorien. Integriert wird dabei jeweils von

bis

.

Zu einer gegebenen Schätzung des erweiterten Variablenvektors

berechnet man die Lösungen

der

unabhängigen Anfangswertprobleme auf jedem Teilintervall

und erhält so eine (zunächst unstetige) Parameterisierung von

. Durch die zusätzlichen Anschlußbedingungen

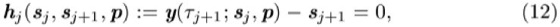
wird die Stetigkeit der Lösung gesichert.

Formal handelt es sich bei dem beschriebenen Ausgleichsproblem um ein beschränktes Optimierungsproblem der Gestalt (10) mit

. Je nach Problemklasse kann die Anzahl der Variablen von unter 100 bis zu mehreren tausend betragen.

Das beschränkte, hochgradig nichtlineare Problem wird wieder mit Hilfe eines verallgemeinerten, gedämpften Gauß-Newton-Verfahrens gelöst. Durch Berücksichtigung der infolge der Bedingungen (12) des Mehrzielansatzes speziellen Form der Matrizen

kann (10) durch einen Kondensierungsalgorithmus auf ein System erheblich niedrigerer Dimension

reduziert werden, aus dem zunächst

und schließlich

bestimmt wird; hierbei treten die Einzelschritte ›Rückwärtsrekursion‹, ›Vorwärtsrekursion‹ und die ›Lösung des kondensierten Problems‹ auf.

Parameteridentifizierungsprobleme in partiellen Differentialgleichungssystemen lassen sich in bestimmten Fällen mit der beschriebenen Methode ebenfalls lösen, indem man das partielle Differentialgleichungssystem mit Hilfe der Methode der Linien (MdL) auf ein System gewöhnlicher Differentialgleichungen zurückführt. Dies entspricht einer Finite-Differenzen oder Finite-Elemente-Diskretisierung im räumlichen Bereich; der zeitliche Bereich wird mit Hilfe des Mehrzielverfahrens diskretisiert. Die MdL wird besonders häufig verwendet bei zeitabhängigen partiellen Differentialgleichungsmodellen mit nur einer räumlichen Variablen. Wie im folgenden Beispiel der Diffusionsgleichung gezeigt, führt die räumliche Diskretisierung auf eine gekoppeltes System von N gewöhnlichen Differentialgleichungen, wenn N die Anzahl der Diskretisierungspunkte bezeichnet. Die Diffusionsgleichung

mit zu bestimmendem, ortsunabhängigem Diffusionskoeffizienten D (weitere Parameter treten in den Randbedingungen auf, sollen hier aber nicht weiter betrachtet werden) erlaubt die räumliche Diskretisierung nach z,

Approximiert man die räumliche Ableitung durch ihre finiten Differenzen

so kann die Diffusionsgleichung durch die

gewöhnlichen Differentialgleichungen

ersetzt und mit Hilfe des oben beschriebenen Verfahrens gelöst werden. Als Anwendungsbeispiel sei die Modellierung und Analyse hygroskopischer Flüssigkeiten genannt, bei denen Diffusionsraten und Stofftransportkonstanten an der Oberfläche bestimmt werden.

Literatur:

C.L. Lawson und R.J. Hanson: Solving Least Square Problems, Prentice Hall, Englewood Cliffs, NJ, 1974.
R.L. Branham: Scientific Data Analysis: An Introduction to Overdetermined Systems, Springer, New York, 1990.
J. Stoer und R. Bulirsch: Einführung in der Numerische Analysis, 1992.
P.E. Gill, W. Murray und M.H. Wright: Practical Optimisation, Academic Press, London, 1981.
H.G. Bock: Randwertproblemmethoden zur Parameteridentifizierung in Systemen nichtlinearer Differentialgleichungen, Universität Heidelberg, 1987.